
Question Number 25462 by Tinkutara last updated on 10/Dec/17
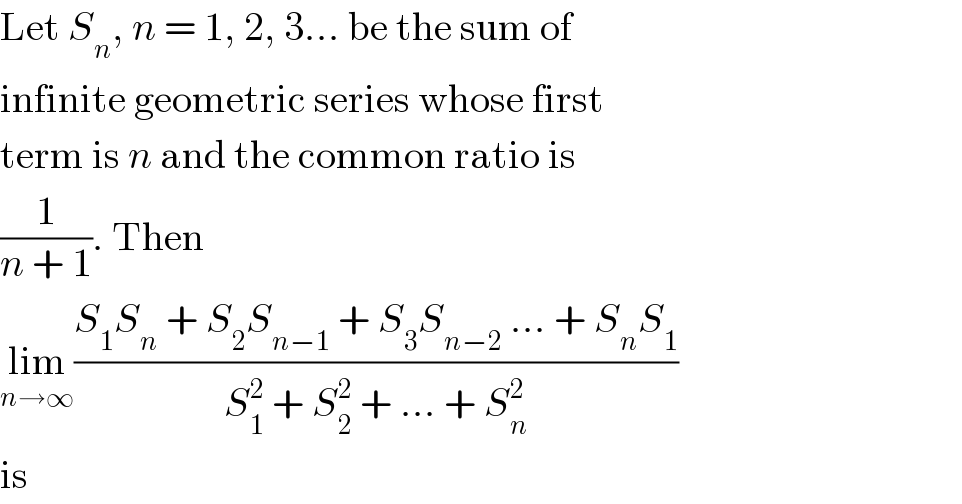
$$\mathrm{Let}\:{S}_{{n}} ,\:{n}\:=\:\mathrm{1},\:\mathrm{2},\:\mathrm{3}...\:\mathrm{be}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{infinite}\:\mathrm{geometric}\:\mathrm{series}\:\mathrm{whose}\:\mathrm{first} \\ $$$$\mathrm{term}\:\mathrm{is}\:{n}\:\mathrm{and}\:\mathrm{the}\:\mathrm{common}\:\mathrm{ratio}\:\mathrm{is} \\ $$$$\frac{\mathrm{1}}{{n}\:+\:\mathrm{1}}.\:\mathrm{Then} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{S}_{\mathrm{1}} {S}_{{n}} \:+\:{S}_{\mathrm{2}} {S}_{{n}−\mathrm{1}} \:+\:{S}_{\mathrm{3}} {S}_{{n}−\mathrm{2}} \:...\:+\:{S}_{{n}} {S}_{\mathrm{1}} }{{S}_{\mathrm{1}} ^{\mathrm{2}} \:+\:{S}_{\mathrm{2}} ^{\mathrm{2}} \:+\:...\:+\:{S}_{{n}} ^{\mathrm{2}} } \\ $$$$\mathrm{is} \\ $$
Answered by ajfour last updated on 11/Dec/17
![S_m =(m/(1−(1/(m+1))))=m+1 Σ_(m=1) ^n S_m ^2 =Σ_(m=1) ^n (m+1)^2 =(((n+1)(n+2)(2n+3))/6)−1 ..(i) S_m S_(n−m+1) =(m+1)(n−m+2) Σ_(m=1) S_m S_(n−m+1) =(n+2)Σ_(m=1) ^n (m+1) −Σ_(m=1) ^n m(m+1) Σ_(m=1) ^n S_m S_(n−m+1) =(n+2)[((n(n+1))/2)+n] −((n(n+1)(n+2))/3) =((n(n+1)(n+2))/6)+n(n+2) ...(ii) using (i) and (ii): lim_(n→∞) ((Σ_(m=1) ^n S_m S_(n−m+) )/(Σ_(m=1) ^n S_m ^2 )) = lim_(n→∞) (([((n(n+1)(n+2))/6)+n(n+2)])/([((n(n+2)(2n+3))/6)−1])) =((coeff. of n^3 in N^r )/(coeff. of n^3 in D^r )) = ((1/6)/(1/3)) =(1/2) .](Q25516.png)
$${S}_{{m}} =\frac{{m}}{\mathrm{1}−\frac{\mathrm{1}}{{m}+\mathrm{1}}}={m}+\mathrm{1} \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{S}_{{m}} ^{\mathrm{2}} =\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left({m}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}{\mathrm{6}}−\mathrm{1}\:\:\:..\left({i}\right) \\ $$$${S}_{{m}} {S}_{{n}−{m}+\mathrm{1}} =\left({m}+\mathrm{1}\right)\left({n}−{m}+\mathrm{2}\right) \\ $$$$\underset{{m}=\mathrm{1}} {\sum}{S}_{{m}} {S}_{{n}−{m}+\mathrm{1}} =\left({n}+\mathrm{2}\right)\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left({m}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{m}\left({m}+\mathrm{1}\right) \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{S}_{{m}} {S}_{{n}−{m}+\mathrm{1}} =\left({n}+\mathrm{2}\right)\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+{n}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$$\:\:\:=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}}+{n}\left({n}+\mathrm{2}\right)\:\:\:...\left({ii}\right) \\ $$$${using}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{S}_{{m}} {S}_{{n}−{m}+} }{\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}{S}_{{m}} ^{\mathrm{2}} }\:= \\ $$$$\:\:\:\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left[\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}}+{n}\left({n}+\mathrm{2}\right)\right]}{\left[\frac{{n}\left({n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}{\mathrm{6}}−\mathrm{1}\right]} \\ $$$$\:\:=\frac{{coeff}.\:{of}\:{n}^{\mathrm{3}} \:{in}\:{N}^{{r}} }{{coeff}.\:{of}\:{n}^{\mathrm{3}} \:{in}\:{D}^{{r}} }\:=\:\frac{\mathrm{1}/\mathrm{6}}{\mathrm{1}/\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by Tinkutara last updated on 11/Dec/17
Thank you Sir!
