Question Number 25605 by behi.8.3.4.17@gmail.com last updated on 11/Dec/17
Commented by behi.8.3.4.17@gmail.com last updated on 12/Dec/17
$$\mathrm{from}\:\mathrm{midpoints}\:\mathrm{of}\:\mathrm{sides}\:\mathrm{draw}\:\mathrm{perpendicular} \\ $$$$\mathrm{lines}\:\mathrm{to}\:\mathrm{opposite}\:\mathrm{sides}.\mathrm{find}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{inner}\:\mathrm{hexagon}\:\mathrm{to}\:\mathrm{area}\:\mathrm{of}:\mathrm{A}\overset{\bigtriangleup} {\mathrm{B}C}. \\ $$
Commented by ajfour last updated on 12/Dec/17
Commented by ajfour last updated on 12/Dec/17
![△ABC=(1/2)(2a)(2c)=2ac △DEF=(1/4)(△ABC)=((ac)/2) △DGF=(1/2)×FM×(MD−GM) =(1/2)×b×(c−(b/(tan C)) )=(b/2)[c−((b(a−b))/c)] =((b(c^2 +b^2 −ab))/(2c)) . △FEB=(1/2)×NF×(EN−IN) =(1/2)(a−b)[c−((a−b)/(tan B))] =(1/2)(a−b)[c−(((a−b)b)/c)] =(((a−b)(c^2 +b^2 −ab))/(2c)) . and y(tan B+tan C)=a ⇒ y=(a/(((c/b)+(c/(a−b))))) =((b(a−b))/c) △HED=(1/2)×a×y =((ab(a−b))/(2c)) Area(hexagon)=Ar(△DEF)+ Ar(△DGF)+Ar(△FEB)+ Ar(△HED) =((ac)/2)+(b/(2c))(c^2 +b^2 −ab)+ (((a−b)(c^2 +b^2 −ab))/(2c))+((ab(a−b))/(2c)) =((ac)/2)+(((c^2 +b^2 −ab)a)/(2c))+(((ab−b^2 )a)/(2c)) =(a/(2c))(c^2 +c^2 ) =ac so ((Ar(hexagon))/(Ar(△ABC)))=((ac)/(2ac)) =(1/2) .](Q25643.png)
$$\bigtriangleup{ABC}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}\right)\left(\mathrm{2}{c}\right)=\mathrm{2}{ac} \\ $$$$\bigtriangleup{DEF}=\frac{\mathrm{1}}{\mathrm{4}}\left(\bigtriangleup{ABC}\right)=\frac{{ac}}{\mathrm{2}} \\ $$$$\bigtriangleup{DGF}=\frac{\mathrm{1}}{\mathrm{2}}×{FM}×\left({MD}−{GM}\right) \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}×{b}×\left({c}−\frac{{b}}{\mathrm{tan}\:{C}}\:\right)=\frac{{b}}{\mathrm{2}}\left[{c}−\frac{{b}\left({a}−{b}\right)}{{c}}\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\boldsymbol{{b}}\left(\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{ab}}\right)}{\mathrm{2}\boldsymbol{{c}}}\:. \\ $$$$\bigtriangleup{FEB}=\frac{\mathrm{1}}{\mathrm{2}}×{NF}×\left({EN}−{IN}\right) \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{b}\right)\left[{c}−\frac{{a}−{b}}{\mathrm{tan}\:{B}}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{b}\right)\left[{c}−\frac{\left({a}−{b}\right){b}}{{c}}\right] \\ $$$$\:\:\:\:=\frac{\left(\boldsymbol{{a}}−\boldsymbol{{b}}\right)\left(\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{ab}}\right)}{\mathrm{2}\boldsymbol{{c}}}\:. \\ $$$$\:{and}\:\:{y}\left(\mathrm{tan}\:{B}+\mathrm{tan}\:{C}\right)={a} \\ $$$$\Rightarrow\:\:\:{y}=\frac{{a}}{\left(\frac{{c}}{{b}}+\frac{{c}}{{a}−{b}}\right)}\:=\frac{{b}\left({a}−{b}\right)}{{c}} \\ $$$$\bigtriangleup{HED}=\frac{\mathrm{1}}{\mathrm{2}}×\boldsymbol{{a}}×\boldsymbol{{y}} \\ $$$$\:\:\:\:\:\:=\frac{{ab}\left({a}−{b}\right)}{\mathrm{2}{c}} \\ $$$${Area}\left({hexagon}\right)={Ar}\left(\bigtriangleup{DEF}\right)+ \\ $$$$\:\:\:\:\:{Ar}\left(\bigtriangleup{DGF}\right)+{Ar}\left(\bigtriangleup{FEB}\right)+ \\ $$$$\:\:\:\:\:{Ar}\left(\bigtriangleup{HED}\right) \\ $$$$\:\:\:\:=\frac{{ac}}{\mathrm{2}}+\frac{{b}}{\mathrm{2}{c}}\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\frac{\left({a}−{b}\right)\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right)}{\mathrm{2}{c}}+\frac{{ab}\left({a}−{b}\right)}{\mathrm{2}{c}} \\ $$$$\:\:\:\:=\frac{{ac}}{\mathrm{2}}+\frac{\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} −{ab}\right){a}}{\mathrm{2}{c}}+\frac{\left({ab}−{b}^{\mathrm{2}} \right){a}}{\mathrm{2}{c}} \\ $$$$\:=\frac{{a}}{\mathrm{2}{c}}\left({c}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\:={ac} \\ $$$${so}\:\:\frac{{Ar}\left({hexagon}\right)}{{Ar}\left(\bigtriangleup{ABC}\right)}=\frac{\boldsymbol{{ac}}}{\mathrm{2}\boldsymbol{{ac}}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by behi.8.3.4.17@gmail.com last updated on 12/Dec/17
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{mr}\:\mathrm{Ajfour}. \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{elegant}\:\mathrm{approach}! \\ $$
Answered by mrW1 last updated on 12/Dec/17
Commented by mrW1 last updated on 12/Dec/17
$${An}\:{other}\:{way}: \\ $$$$\Delta{DEF}=\frac{\mathrm{1}}{\mathrm{4}}\Delta{ABC} \\ $$$$\Delta{DIE}=\Delta{AGF}=\Delta{FHC} \\ $$$$\Delta{FGD}=\Delta{CHE}=\Delta{EIB} \\ $$$$\Delta{EHF}=\Delta{BID}=\Delta{DGA} \\ $$$$\Rightarrow\Delta{DIE}+\Delta{FGD}+\Delta{EHF}=\Delta{BDE}=\frac{\mathrm{1}}{\mathrm{4}}\Delta{ABC} \\ $$$${A}_{{HEXAGON}} =\Delta{DEF}+\Delta{DIE}+\Delta{FGD}+\Delta{EHF} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\Delta{ABC} \\ $$
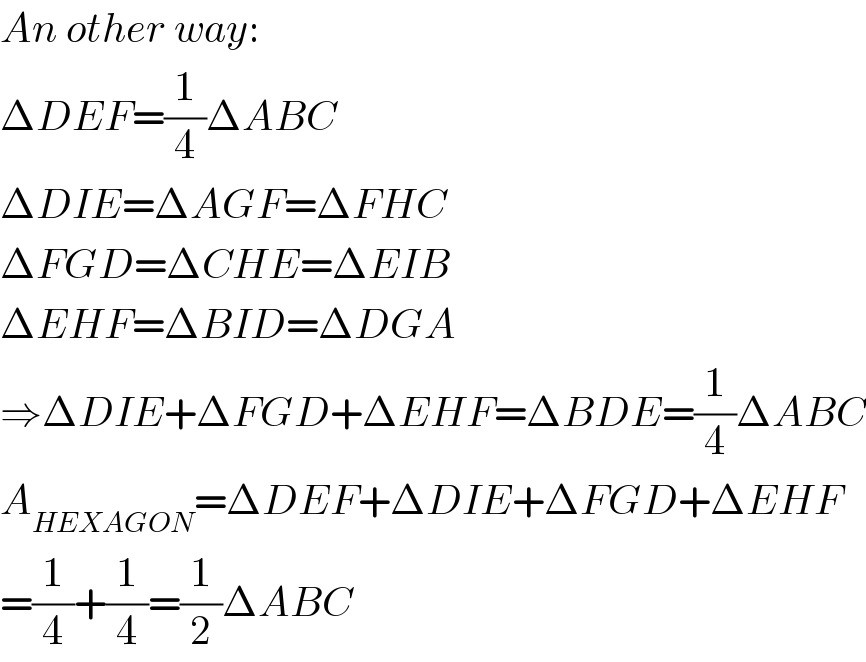
Commented by ajfour last updated on 12/Dec/17
$${elegant}\:{shading}\:{Sir}! \\ $$
Commented by behi.8.3.4.17@gmail.com last updated on 12/Dec/17
$$\mathrm{Hi}\:\mathrm{dear}\:\mathrm{master}.\mathrm{as}\:\mathrm{mr}\:\mathrm{Ajfour}\:\mathrm{said},\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{beautiful}\:\mathrm{and}\:\mathrm{smart}\:\mathrm{solution}.\mathrm{thanks}. \\ $$