Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 26020 by abdo imad last updated on 17/Dec/17

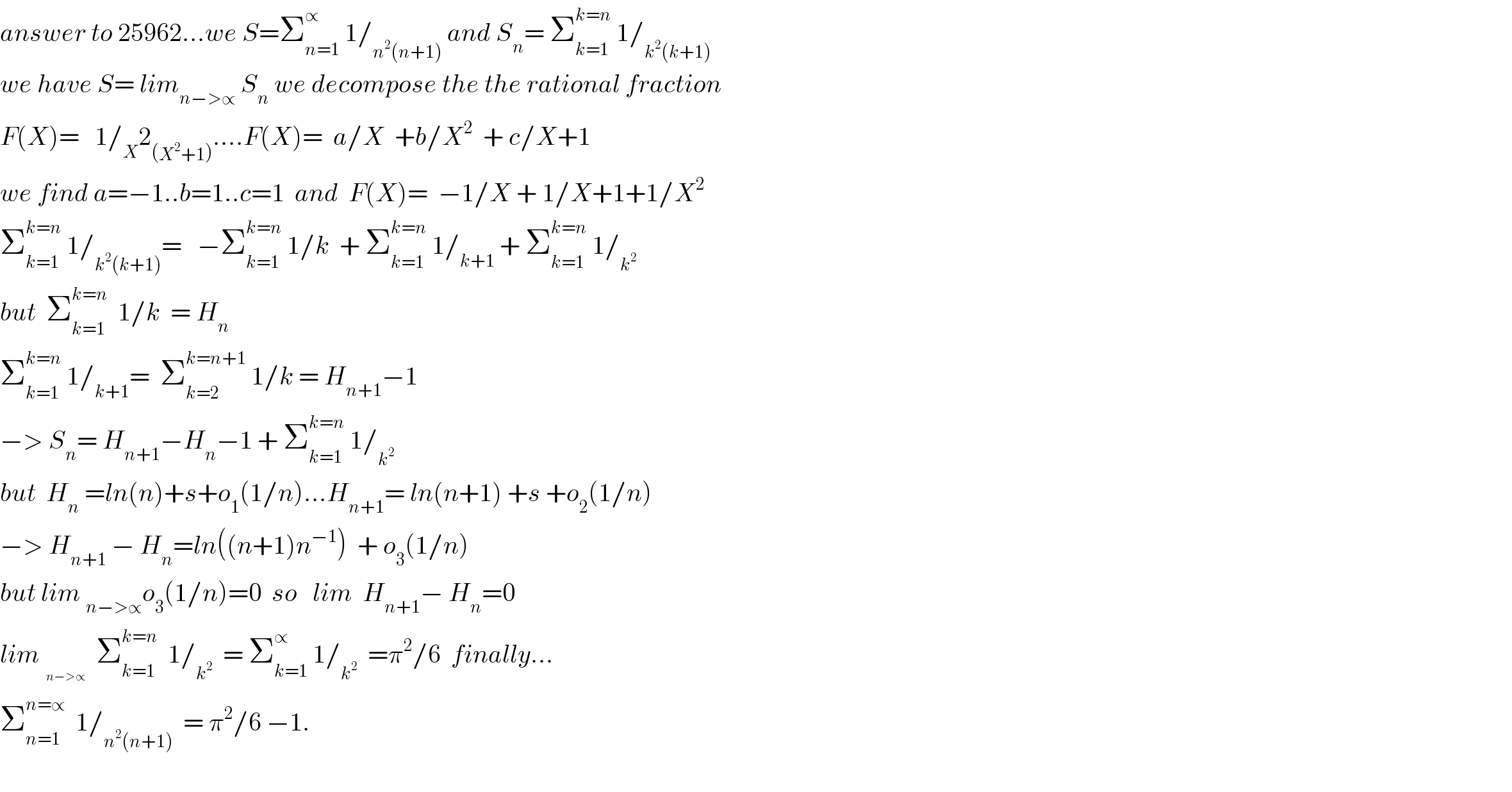
answer to 25962...we S=Σ_(n=1) ^∝ 1/_(n^2 (n+1)) and S_n = Σ_(k=1) ^(k=n) 1/_(k^2 (k+1)) we have S= lim_(n−>∝) S_n we decompose the the rational fraction F(X)= 1/_X 2_((X^2 +1)) ....F(X)= a/X +b/X^2 + c/X+1 we find a=−1..b=1..c=1 and F(X)= −1/X + 1/X+1+1/X^2 Σ_(k=1) ^(k=n) 1/_(k^2 (k+1)) = −Σ_(k=1) ^(k=n) 1/k + Σ_(k=1) ^(k=n) 1/_(k+1) + Σ_(k=1) ^(k=n) 1/_k^2 but Σ_(k=1) ^(k=n) 1/k = H_n Σ_(k=1) ^(k=n) 1/_(k+1) = Σ_(k=2) ^(k=n+1) 1/k = H_(n+1) −1 −> S_n = H_(n+1) −H_n −1 + Σ_(k=1) ^(k=n) 1/_k^2 but H_n =ln(n)+s+o_1 (1/n)...H_(n+1) = ln(n+1) +s +o_2 (1/n) −> H_(n+1) − H_n =ln((n+1)n^(−1) ) + o_3 (1/n) but lim _(n−>∝) o_3 (1/n)=0 so lim H_(n+1) − H_n =0 lim_ Σ_(k=1) ^(k=n) 1/_k^2 = Σ_(k=1) ^∝ 1/_k^2 =π^2 /6 finally... Σ_(n=1) ^(n=∝) 1/_(n^2 (n+1)) = π^2 /6 −1.

$${answer}\:{to}\:\mathrm{25962}...{we}\:{S}=\sum_{{n}=\mathrm{1}} ^{\propto} \:\mathrm{1}/_{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \:{and}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} \\ $$ $${we}\:{have}\:{S}=\:{lim}_{{n}−>\propto} \:{S}_{{n}} \:{we}\:{decompose}\:{the}\:{the}\:{rational}\:{fraction} \\ $$ $${F}\left({X}\right)=\:\:\:\mathrm{1}/_{{X}} \mathrm{2}_{\left({X}^{\mathrm{2}} +\mathrm{1}\right)} ....{F}\left({X}\right)=\:\:{a}/{X}\:\:+{b}/{X}^{\mathrm{2}} \:\:+\:{c}/{X}+\mathrm{1} \\ $$ $${we}\:{find}\:{a}=−\mathrm{1}..{b}=\mathrm{1}..{c}=\mathrm{1}\:\:{and}\:\:{F}\left({X}\right)=\:\:−\mathrm{1}/{X}\:+\:\mathrm{1}/{X}+\mathrm{1}+\mathrm{1}/{X}^{\mathrm{2}} \\ $$ $$\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)} =\:\:\:−\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/{k}\:\:+\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}+\mathrm{1}} \:+\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}^{\mathrm{2}} } \\ $$ $${but}\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\mathrm{1}/{k}\:\:=\:{H}_{{n}} \\ $$ $$\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}+\mathrm{1}} =\:\:\sum_{{k}=\mathrm{2}} ^{{k}={n}+\mathrm{1}} \:\mathrm{1}/{k}\:=\:{H}_{{n}+\mathrm{1}} −\mathrm{1} \\ $$ $$−>\:{S}_{{n}} =\:{H}_{{n}+\mathrm{1}} −{H}_{{n}} −\mathrm{1}\:+\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\mathrm{1}/_{{k}^{\mathrm{2}} } \\ $$ $${but}\:\:{H}_{{n}} \:={ln}\left({n}\right)+{s}+{o}_{\mathrm{1}} \left(\mathrm{1}/{n}\right)...{H}_{{n}+\mathrm{1}} =\:{ln}\left({n}+\mathrm{1}\right)\:+{s}\:+{o}_{\mathrm{2}} \left(\mathrm{1}/{n}\right) \\ $$ $$−>\:{H}_{{n}+\mathrm{1}} \:−\:{H}_{{n}} ={ln}\left(\left({n}+\mathrm{1}\right){n}^{−\mathrm{1}} \right)\:\:+\:{o}_{\mathrm{3}} \left(\mathrm{1}/{n}\right) \\ $$ $${but}\:{lim}\:_{{n}−>\propto} {o}_{\mathrm{3}} \left(\mathrm{1}/{n}\right)=\mathrm{0}\:\:{so}\:\:\:{lim}\:\:{H}_{{n}+\mathrm{1}} −\:{H}_{{n}} =\mathrm{0} \\ $$ $${lim}_{} \:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\mathrm{1}/_{{k}^{\mathrm{2}} } \:\:=\:\sum_{{k}=\mathrm{1}} ^{\propto} \:\mathrm{1}/_{{k}^{\mathrm{2}} } \:\:=\pi^{\mathrm{2}} /\mathrm{6}\:\:{finally}... \\ $$ $$\sum_{{n}=\mathrm{1}} ^{{n}=\propto} \:\:\mathrm{1}/_{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \:\:=\:\pi^{\mathrm{2}} /\mathrm{6}\:−\mathrm{1}. \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com