
Question Number 26021 by ajfour last updated on 17/Dec/17

Commented by ajfour last updated on 17/Dec/17

$${If}\:{a}\:{ray}\:{of}\:{light}\:{from}\:{P}\left({a},{b}\right)\:{has} \\ $$$${to}\:{return}\:{back}\:{to}\:{P}\:{upon}\:{two}\: \\ $$$${reflections},\:{from}\:{parabola}\:{y}={x}^{\mathrm{2}} , \\ $$$${say}\:{at}\:{points}\:{B}\:{and}\:{C}.\:{Then}\:{find} \\ $$$${coordinates}\:{of}\:{B}\:{and}\:{C}\:{in}\:{terms} \\ $$$${of}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}. \\ $$
Answered by mrW1 last updated on 17/Dec/17

Commented by mrW1 last updated on 18/Dec/17
![y=f(x)=x^2 f′(x)=2x T_1 and T_2 =tangent line at A and B P_1 (x_1 ,y_1 )=mirror image of P on T_1 P_2 (x_2 ,y_2 )=mirror image of P on T_2 P_1 , A, B and P_2 must collinear. A(x_A ,y_A ) with y_A =x_A ^2 B(x_B ,y_B ) with y_B =x_B ^2 Eqn. of T_1 : ((y−y_A )/(x−x_A ))=f′(x_A )=2x_A ⇒−2x_A x+y+x_A ^2 =0 Eqn. of T_2 : ⇒−2x_B x+y+x_B ^2 =0 PP_1 : (x,y)=(a,b)+λ(−2x_A ,1) −2x_A (a−2x_A λ)+(b+λ)+x_A ^2 =0 ⇒λ=((2ax_A −x_A ^2 −b)/(1+4x_A ^2 ))=((a^2 −b−(a−x_A )^2 )/(1+4x_A ^2 )) ⇒x_1 =a+2λ(−2x_A )=a−4x_A ×((a^2 −b−(a−x_A )^2 )/(1+4x_A ^2 )) ⇒y_1 =b+2λ=b+2×((a^2 −b−(a−x_A )^2 )/(1+4x_A ^2 )) similarily: ⇒x_2 =a−4x_B ×((a^2 −b−(a−x_B )^2 )/(1+4x_B ^2 )) ⇒y_2 =b+2×((a^2 −b−(a−x_B )^2 )/(1+4x_B ^2 )) P_1 ,A,B are collinear: ((y_1 −y_A )/(x_1 −x_A ))=((y_A −y_B )/(x_A −x_B ))=((x_A ^2 −x_B ^2 )/(x_A −x_B ))=x_A +x_B ⇒y_1 −y_A =(x_A +x_B )(x_1 −x_A ) b+2×((a^2 −b−(a−x_A )^2 )/(1+4x_A ^2 ))−y_A =(x_A +x_B )(a−4x_A ×((a^2 −b−(a−x_A )^2 )/(1+4x_A ^2 ))−x_A ) (b−y_A )(1+4x_A ^2 )+2[(a^2 −b)−(a−x_A )^2 ]=(x_A +x_B ){(a−x_A )(1+4x_A ^2 )−4x_A [(a^2 −b)−(a−x_A )^2 ]} ⇒(b−x_A ^2 )(1+4x_A ^2 )+2[(a^2 −b)−(a−x_A )^2 ]=(x_A +x_B ){(a−x_A )(1+4x_A ^2 )−4x_A [(a^2 −b)−(a−x_A )^2 ]} ...(i) similarily: ⇒(b−x_B ^2 )(1+4x_B ^2 )+2[(a^2 −b)−(a−x_B )^2 ]=(x_B +x_A ){(a−x_B )(1+4x_B ^2 )−4x_B [(a^2 −b)−(a−x_B )^2 ]} ...(ii) ⇒(((b−x_A ^2 )(1+4x_A ^2 )+2[(a^2 −b)−(a−x_A )^2 ])/((b−x_B ^2 )(1+4x_B ^2 )+2[(a^2 −b)−(a−x_B )^2 ]))=(((a−x_A )(1+4x_A ^2 )−4x_A [(a^2 −b)−(a−x_A )^2 ])/((a−x_B )(1+4x_B ^2 )−4x_B [(a^2 −b)−(a−x_B )^2 ])) .....](Q26026.png)
$${y}={f}\left({x}\right)={x}^{\mathrm{2}} \\ $$$${f}'\left({x}\right)=\mathrm{2}{x} \\ $$$${T}_{\mathrm{1}} \:{and}\:{T}_{\mathrm{2}} ={tangent}\:{line}\:{at}\:{A}\:{and}\:{B} \\ $$$${P}_{\mathrm{1}} \left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)={mirror}\:{image}\:{of}\:{P}\:{on}\:{T}_{\mathrm{1}} \\ $$$${P}_{\mathrm{2}} \left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)={mirror}\:{image}\:{of}\:{P}\:{on}\:{T}_{\mathrm{2}} \\ $$$${P}_{\mathrm{1}} ,\:{A},\:{B}\:{and}\:{P}_{\mathrm{2}} \:{must}\:{collinear}. \\ $$$${A}\left({x}_{{A}} ,{y}_{{A}} \right)\:{with}\:{y}_{{A}} ={x}_{{A}} ^{\mathrm{2}} \\ $$$${B}\left({x}_{{B}} ,{y}_{{B}} \right)\:{with}\:{y}_{{B}} ={x}_{{B}} ^{\mathrm{2}} \\ $$$${Eqn}.\:{of}\:{T}_{\mathrm{1}} : \\ $$$$\frac{{y}−{y}_{{A}} }{{x}−{x}_{{A}} }={f}'\left({x}_{{A}} \right)=\mathrm{2}{x}_{{A}} \\ $$$$\Rightarrow−\mathrm{2}{x}_{{A}} {x}+{y}+{x}_{{A}} ^{\mathrm{2}} =\mathrm{0} \\ $$$${Eqn}.\:{of}\:{T}_{\mathrm{2}} : \\ $$$$\Rightarrow−\mathrm{2}{x}_{{B}} {x}+{y}+{x}_{{B}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${PP}_{\mathrm{1}} :\:\left({x},{y}\right)=\left({a},{b}\right)+\lambda\left(−\mathrm{2}{x}_{{A}} ,\mathrm{1}\right) \\ $$$$−\mathrm{2}{x}_{{A}} \left({a}−\mathrm{2}{x}_{{A}} \lambda\right)+\left({b}+\lambda\right)+{x}_{{A}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{2}{ax}_{{A}} −{x}_{{A}} ^{\mathrm{2}} −{b}}{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} } \\ $$$$\Rightarrow{x}_{\mathrm{1}} ={a}+\mathrm{2}\lambda\left(−\mathrm{2}{x}_{{A}} \right)={a}−\mathrm{4}{x}_{{A}} ×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} } \\ $$$$\Rightarrow{y}_{\mathrm{1}} ={b}+\mathrm{2}\lambda={b}+\mathrm{2}×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} } \\ $$$${similarily}: \\ $$$$\Rightarrow{x}_{\mathrm{2}} ={a}−\mathrm{4}{x}_{{B}} ×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} } \\ $$$$\Rightarrow{y}_{\mathrm{2}} ={b}+\mathrm{2}×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} } \\ $$$$ \\ $$$${P}_{\mathrm{1}} ,{A},{B}\:{are}\:{collinear}: \\ $$$$\frac{{y}_{\mathrm{1}} −{y}_{{A}} }{{x}_{\mathrm{1}} −{x}_{{A}} }=\frac{{y}_{{A}} −{y}_{{B}} }{{x}_{{A}} −{x}_{{B}} }=\frac{{x}_{{A}} ^{\mathrm{2}} −{x}_{{B}} ^{\mathrm{2}} }{{x}_{{A}} −{x}_{{B}} }={x}_{{A}} +{x}_{{B}} \\ $$$$\Rightarrow{y}_{\mathrm{1}} −{y}_{{A}} =\left({x}_{{A}} +{x}_{{B}} \right)\left({x}_{\mathrm{1}} −{x}_{{A}} \right) \\ $$$${b}+\mathrm{2}×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} }−{y}_{{A}} =\left({x}_{{A}} +{x}_{{B}} \right)\left({a}−\mathrm{4}{x}_{{A}} ×\frac{{a}^{\mathrm{2}} −{b}−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} }−{x}_{{A}} \right) \\ $$$$\left({b}−{y}_{{A}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]=\left({x}_{{A}} +{x}_{{B}} \right)\left\{\left({a}−{x}_{{A}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{A}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]\right\} \\ $$$$\Rightarrow\left({b}−{x}_{{A}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]=\left({x}_{{A}} +{x}_{{B}} \right)\left\{\left({a}−{x}_{{A}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{A}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]\right\}\:\:\:...\left({i}\right) \\ $$$${similarily}: \\ $$$$\Rightarrow\left({b}−{x}_{{B}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} \right]=\left({x}_{{B}} +{x}_{{A}} \right)\left\{\left({a}−{x}_{{B}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{B}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} \right]\right\}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$$\Rightarrow\frac{\left({b}−{x}_{{A}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]}{\left({b}−{x}_{{B}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} \right]}=\frac{\left({a}−{x}_{{A}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{A}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]}{\left({a}−{x}_{{B}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{B}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{B}} \right)^{\mathrm{2}} \right]} \\ $$$$..... \\ $$
Commented by ajfour last updated on 18/Dec/17
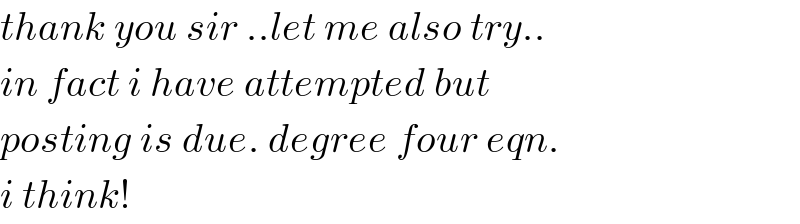
$${thank}\:{you}\:{sir}\:..{let}\:{me}\:{also}\:{try}.. \\ $$$${in}\:{fact}\:{i}\:{have}\:{attempted}\:{but}\: \\ $$$${posting}\:{is}\:{due}.\:{degree}\:{four}\:{eqn}. \\ $$$${i}\:{think}! \\ $$
Commented by mrW1 last updated on 18/Dec/17
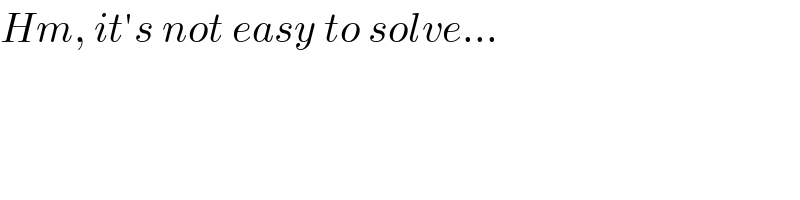
$${Hm},\:{it}'{s}\:{not}\:{easy}\:{to}\:{solve}... \\ $$
Commented by ajfour last updated on 19/Dec/17
![i got: ((b−x_B ^2 )/(a−x_B ))=((x_B [3+4x_B (x_A +x_B )]−x_A )/(1+4x_A x_B )) and the similar eq. with x_A interchanged with x_B . what value of x_B can your expeession yield Sir, if a=0 and x_B =−x_A ?](Q26101.png)
$${i}\:{got}: \\ $$$$\frac{{b}−{x}_{{B}} ^{\mathrm{2}} }{{a}−{x}_{{B}} }=\frac{{x}_{{B}} \left[\mathrm{3}+\mathrm{4}{x}_{{B}} \left({x}_{{A}} +{x}_{{B}} \right)\right]−{x}_{{A}} }{\mathrm{1}+\mathrm{4}{x}_{{A}} {x}_{{B}} } \\ $$$$\:{and}\:{the}\:{similar}\:{eq}.\:{with}\:{x}_{{A}} \: \\ $$$${interchanged}\:{with}\:{x}_{{B}} . \\ $$$${what}\:{value}\:{of}\:{x}_{{B}} \:{can}\:{your}\: \\ $$$${expeession}\:{yield}\:{Sir},\:{if}\:{a}=\mathrm{0} \\ $$$${and}\:{x}_{{B}} =−{x}_{{A}} \:? \\ $$
Commented by mrW1 last updated on 19/Dec/17
![(b−x_A ^2 )(1+4x_A ^2 )+2[(a^2 −b)−(a−x_A )^2 ]=(x_A +x_B ){(a−x_A )(1+4x_A ^2 )−4x_A [(a^2 −b)−(a−x_A )^2 ]} ...(i) with a=0 and x_A =−x_B we get (b−x_B ^2 )(1+4x_B ^2 )+2(−b−x_B ^2 )=0 b−x_B ^2 +4bx_B ^2 −4x_B ^4 −2b−2x_B ^2 =0 4x_B ^4 −(4b−3)x_B ^2 +b=0 ⇒x_B ^2 =((4b−3±(√((4b−3)^2 −16b)))/8) ⇒x_B ^2 =((4b−3±(√((4b−1)(4b−9))))/8) ⇒b≥(9/4)](Q26103.png)
$$\left({b}−{x}_{{A}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)+\mathrm{2}\left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]=\left({x}_{{A}} +{x}_{{B}} \right)\left\{\left({a}−{x}_{{A}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{A}} ^{\mathrm{2}} \right)−\mathrm{4}{x}_{{A}} \left[\left({a}^{\mathrm{2}} −{b}\right)−\left({a}−{x}_{{A}} \right)^{\mathrm{2}} \right]\right\}\:\:\:...\left({i}\right) \\ $$$${with}\:{a}=\mathrm{0}\:{and}\:{x}_{{A}} =−{x}_{{B}} \:{we}\:{get} \\ $$$$\left({b}−{x}_{{B}} ^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{4}{x}_{{B}} ^{\mathrm{2}} \right)+\mathrm{2}\left(−{b}−{x}_{{B}} ^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${b}−{x}_{{B}} ^{\mathrm{2}} +\mathrm{4}{bx}_{{B}} ^{\mathrm{2}} −\mathrm{4}{x}_{{B}} ^{\mathrm{4}} −\mathrm{2}{b}−\mathrm{2}{x}_{{B}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{x}_{{B}} ^{\mathrm{4}} −\left(\mathrm{4}{b}−\mathrm{3}\right){x}_{{B}} ^{\mathrm{2}} +{b}=\mathrm{0} \\ $$$$\Rightarrow{x}_{{B}} ^{\mathrm{2}} =\frac{\mathrm{4}{b}−\mathrm{3}\pm\sqrt{\left(\mathrm{4}{b}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{16}{b}}}{\mathrm{8}} \\ $$$$\Rightarrow{x}_{{B}} ^{\mathrm{2}} =\frac{\mathrm{4}{b}−\mathrm{3}\pm\sqrt{\left(\mathrm{4}{b}−\mathrm{1}\right)\left(\mathrm{4}{b}−\mathrm{9}\right)}}{\mathrm{8}} \\ $$$$\Rightarrow{b}\geqslant\frac{\mathrm{9}}{\mathrm{4}} \\ $$
Commented by mrW1 last updated on 19/Dec/17
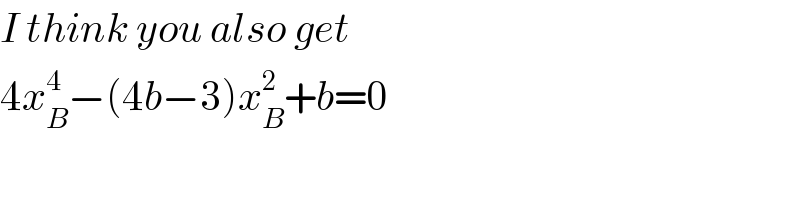
$${I}\:{think}\:{you}\:{also}\:{get} \\ $$$$\mathrm{4}{x}_{{B}} ^{\mathrm{4}} −\left(\mathrm{4}{b}−\mathrm{3}\right){x}_{{B}} ^{\mathrm{2}} +{b}=\mathrm{0} \\ $$
Commented by ajfour last updated on 19/Dec/17

$${yes}\:{sir}!\:{thanks}\:{for}\:{checking}. \\ $$
