Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 26050 by Tinkutara last updated on 18/Dec/17

Answered by ajfour last updated on 20/Dec/17

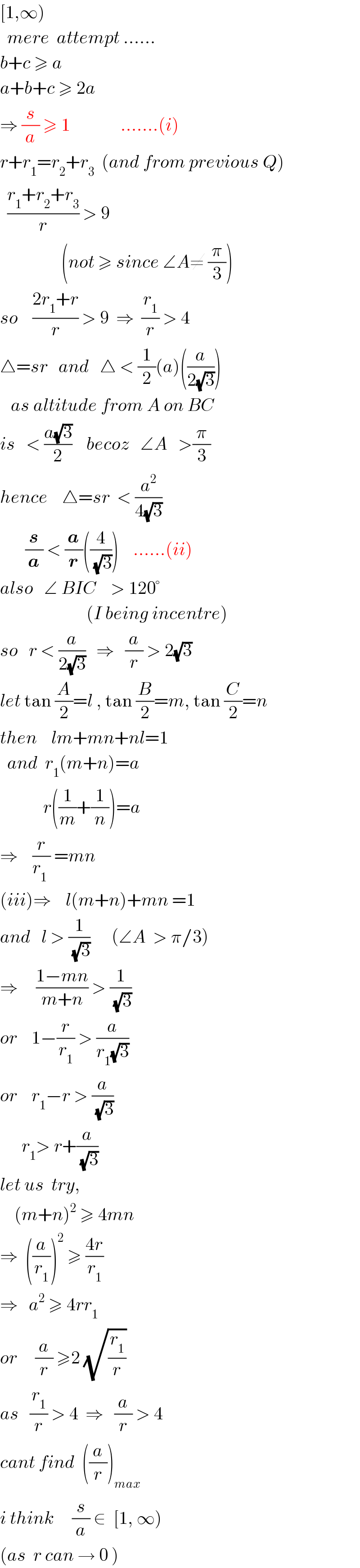
[1,∞) mere attempt ...... b+c ≥ a a+b+c ≥ 2a ⇒ (s/a) ≥ 1 .......(i) r+r_1 =r_2 +r_3 (and from previous Q) ((r_1 +r_2 +r_3 )/r) > 9 (not ≥ since ∠A≠ (π/3)) so ((2r_1 +r)/r) > 9 ⇒ (r_1 /r) > 4 △=sr and △ < (1/2)(a)((a/(2(√3)))) as altitude from A on BC is < ((a(√3))/2) becoz ∠A >(π/3) hence △=sr < (a^2 /(4(√3))) (s/a) < (a/r)((4/(√3))) ......(ii) also ∠ BIC > 120° (I being incentre) so r < (a/(2(√3))) ⇒ (a/r) > 2(√3) let tan (A/2)=l , tan (B/2)=m, tan (C/2)=n then lm+mn+nl=1 and r_1 (m+n)=a r((1/m)+(1/n))=a ⇒ (r/(r_1 )) =mn (iii)⇒ l(m+n)+mn =1 and l > (1/(√3)) (∠A > π/3) ⇒ ((1−mn)/(m+n)) > (1/(√3)) or 1−(r/r_1 ) > (a/(r_1 (√3))) or r_1 −r > (a/(√3)) r_1 > r+(a/(√3)) let us try, (m+n)^2 ≥ 4mn ⇒ ((a/r_1 ))^2 ≥ ((4r)/r_1 ) ⇒ a^2 ≥ 4rr_1 or (a/r) ≥2 (√(r_1 /r)) as (r_1 /r) > 4 ⇒ (a/r) > 4 cant find ((a/r))_(max) i think (s/a) ∈ [1, ∞) (as r can → 0 )

$$\left[\mathrm{1},\infty\right) \\ $$$$\:\:{mere}\:\:{attempt}\:...... \\ $$$${b}+{c}\:\geqslant\:{a} \\ $$$${a}+{b}+{c}\:\geqslant\:\mathrm{2}{a} \\ $$$$\Rightarrow\:\frac{{s}}{{a}}\:\geqslant\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:.......\left({i}\right) \\ $$$${r}+{r}_{\mathrm{1}} ={r}_{\mathrm{2}} +{r}_{\mathrm{3}} \:\:\left({and}\:{from}\:{previous}\:{Q}\right) \\ $$$$\:\:\frac{{r}_{\mathrm{1}} +{r}_{\mathrm{2}} +{r}_{\mathrm{3}} }{{r}}\:>\:\mathrm{9}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({not}\:\geqslant\:{since}\:\angle{A}\neq\:\frac{\pi}{\mathrm{3}}\right) \\ $$$${so}\:\:\:\:\frac{\mathrm{2}{r}_{\mathrm{1}} +{r}}{{r}}\:>\:\mathrm{9}\:\:\Rightarrow\:\:\frac{{r}_{\mathrm{1}} }{{r}}\:>\:\mathrm{4} \\ $$$$\bigtriangleup={sr}\:\:\:{and}\:\:\:\bigtriangleup\:<\:\frac{\mathrm{1}}{\mathrm{2}}\left({a}\right)\left(\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\right) \\ $$$$\:\:\:{as}\:{altitude}\:{from}\:{A}\:{on}\:{BC} \\ $$$${is}\:\:\:<\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:{becoz}\:\:\:\angle{A}\:\:\:>\frac{\pi}{\mathrm{3}} \\ $$$${hence}\:\:\:\:\bigtriangleup={sr}\:\:<\:\frac{{a}^{\mathrm{2}} }{\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\frac{\boldsymbol{{s}}}{\boldsymbol{{a}}}\:<\:\frac{\boldsymbol{{a}}}{\boldsymbol{{r}}}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}\right)\:\:\:\:......\left({ii}\right) \\ $$$${also}\:\:\:\angle\:{BIC}\:\:\:\:>\:\mathrm{120}°\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({I}\:{being}\:{incentre}\right) \\ $$$${so}\:\:\:{r}\:<\:\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\:\Rightarrow\:\:\:\frac{{a}}{{r}}\:>\:\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$${let}\:\mathrm{tan}\:\frac{{A}}{\mathrm{2}}={l}\:,\:\mathrm{tan}\:\frac{{B}}{\mathrm{2}}={m},\:\mathrm{tan}\:\frac{{C}}{\mathrm{2}}={n} \\ $$$${then}\:\:\:\:{lm}+{mn}+{nl}=\mathrm{1}\:\: \\ $$$$\:\:{and}\:\:{r}_{\mathrm{1}} \left({m}+{n}\right)={a}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{r}\left(\frac{\mathrm{1}}{{m}}+\frac{\mathrm{1}}{{n}}\right)={a} \\ $$$$\Rightarrow\:\:\:\:\frac{{r}}{{r}_{\mathrm{1}} \:}\:={mn}\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left({iii}\right)\Rightarrow\:\:\:\:{l}\left({m}+{n}\right)+{mn}\:=\mathrm{1} \\ $$$${and}\:\:\:{l}\:>\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:\:\:\:\:\:\left(\angle{A}\:\:>\:\pi/\mathrm{3}\right) \\ $$$$\Rightarrow\:\:\:\:\:\frac{\mathrm{1}−{mn}}{{m}+{n}}\:>\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\: \\ $$$${or}\:\:\:\:\mathrm{1}−\frac{{r}}{{r}_{\mathrm{1}} }\:>\:\frac{{a}}{{r}_{\mathrm{1}} \sqrt{\mathrm{3}}} \\ $$$${or}\:\:\:\:{r}_{\mathrm{1}} −{r}\:>\:\frac{{a}}{\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:{r}_{\mathrm{1}} >\:{r}+\frac{{a}}{\sqrt{\mathrm{3}}}\:\:\:\:\:\:\:\:\:\: \\ $$$${let}\:{us}\:\:{try}, \\ $$$$\:\:\:\:\left({m}+{n}\right)^{\mathrm{2}} \:\geqslant\:\mathrm{4}{mn} \\ $$$$\Rightarrow\:\:\left(\frac{{a}}{{r}_{\mathrm{1}} }\right)^{\mathrm{2}} \:\geqslant\:\frac{\mathrm{4}{r}}{{r}_{\mathrm{1}} } \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} \:\geqslant\:\mathrm{4}{rr}_{\mathrm{1}} \\ $$$${or}\:\:\:\:\:\frac{{a}}{{r}}\:\geqslant\mathrm{2}\:\sqrt{\frac{{r}_{\mathrm{1}} }{{r}}}\: \\ $$$${as}\:\:\:\frac{{r}_{\mathrm{1}} }{{r}}\:>\:\mathrm{4}\:\:\Rightarrow\:\:\:\frac{{a}}{{r}}\:>\:\mathrm{4} \\ $$$${cant}\:{find}\:\:\left(\frac{{a}}{{r}}\right)_{{max}} \\ $$$${i}\:{think}\:\:\:\:\:\frac{{s}}{{a}}\:\in\:\:\left[\mathrm{1},\:\infty\right) \\ $$$$\left({as}\:\:{r}\:{can}\:\rightarrow\:\mathrm{0}\:\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com