Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 26192 by abdo imad last updated on 22/Dec/17

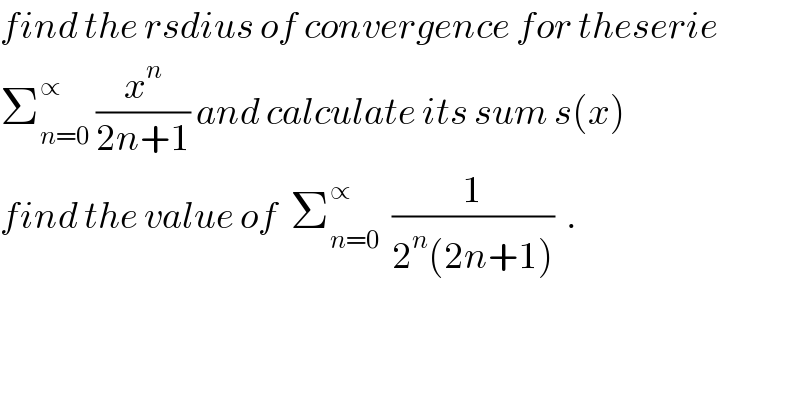
find the rsdius of convergence for theserie Σ_(n=0) ^∝ (x^n /(2n+1)) and calculate its sum s(x) find the value of Σ_(n=0) ^∝ (1/(2^n (2n+1))) .

$${find}\:{the}\:{rsdius}\:{of}\:{convergence}\:{for}\:{theserie} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{and}\:{calculate}\:{its}\:{sum}\:{s}\left({x}\right) \\ $$$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\:\:. \\ $$

Commented by prakash jain last updated on 22/Dec/17

ratio test lim_(n→∞) ∣(x^(n+1) /(2n+1))∙((2n)/x^n )∣=∣x∣lim_(n→∞) ((2n)/(2n+1))=∣x∣ ∣x∣<1 ⇒series converges ∣x∣>1⇒series diverges ____ x=1 Σ_(n=0) ^∞ (1/(2n+1)) , we know it diverges radius of convergence ∣x∣<1

$${ratio}\:{test} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid\frac{{x}^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\centerdot\frac{\mathrm{2}{n}}{{x}^{{n}} }\mid=\mid{x}\mid\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}=\mid{x}\mid \\ $$$$\mid{x}\mid<\mathrm{1}\:\Rightarrow\mathrm{series}\:\mathrm{converges} \\ $$$$\mid{x}\mid>\mathrm{1}\Rightarrow\mathrm{series}\:\mathrm{diverges} \\ $$$$\_\_\_\_ \\ $$$${x}=\mathrm{1} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:,\:\mathrm{we}\:\mathrm{know}\:\mathrm{it}\:\mathrm{diverges} \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{convergence}\:\mid{x}\mid<\mathrm{1} \\ $$

Commented by abdo imad last updated on 22/Dec/17

let put a_n (x) = ((x^n )/(2n+1 )) per x not0 /((a_(n+1) (x))/(a_n (x)))/=/ (x^(n+1) /(2n+3)) ((x^n /(2n+1)))^(−1) / =/((2n+1)/(2n+3))x/ = ((2n+1)/(2n+3))/x/ and lim_(n−>∝) / ((a_(n+1) (x))/a_(n(x)) )/= /x/⇒ if /x/<1 the serie is convergent if /x/>1 the serie diverge if x=1 also the serie diverge if x=−1 Σ_(n≥0) (((−1)^n )/(2n+1)) is convergent because its a alterne serie et S(x)= Σ_(n=0) ^(∝ ) (x^n /(2n+1)) the sum for /x/<1 case1 0<x<1 S(x) = Σ_(n=0) ^∝ ((((√x))^(2n) )/(2n+1)) = (1/(√x)) Σ_(n=0) ^∝ ((((√x))^(2n+1) )/(2n+1)) = (1/(√x)) ϕ((√x))with ϕ(t) = Σ_(n=0) ^∝ (t^(2n+1) /(2n+1)) and /t/<1 ∂ϕ/∂t = Σ_(n=0) ^∝ t^(2n) = (1/(1−t^2 )) ⇒ ϕ(t) =∫ (dt/(1−t^2 )) +λ =(1/2)ln/((1+t)/(1−t))/+λ λ=ϕ(0)=0⇒ S(x)= (1/(2(√x)))ln(((1+(√x))/(1−(√x))) ) case2 −1<x<0 S(x)= Σ_(n=0) ^(∝ ) (((−1)^n ((√(−x)))^(2n) )/(2n+1)) = (1/(√(−x))) Σ_(n=0) ^∝ (((−1)^n ((√(−x)))^(2n+1) )/(2n+1))= (1/(√(−x)))ψ((√(−x))) with ψ(t)= Σ_(n=0) ^∝ (((−1)^n t^(2n+1) )/(2n+1)) and /t/<1 ∂ψ/∂t = Σ_(n=0) ^∝ (−1)^n t^(2n) = Σ_(n=0) ^∝ (−t^2 )^n = (1/(1+t^2 )) ⇒ ψ(t)= ∫ (dt/(1+t^2 )) +κ = arctant +κ k=ψ(0)=0⇒ S(x)= ((artan((√(−x))))/(√(−x))) . value of S= Σ_(n=0) ^∝ (1/(2^n (2n+1))) we have proved that Σ_(n=0) ^∝ (x^n /(2n+1)) =(1/(2(√x))) ln(((1+(√x))/(1−(√x)))) if 0x<1 we take x=(1/2)⇒ S= (1/(2(√(1/2))))ln( ((1+(√(1/2)))/(1−(√(1/2))))) =(1/(√2)) ln(((1+(√2))/(−1+(√2))))

$${let}\:{put}\:\:{a}_{{n}} \left({x}\right)\:\:=\:\frac{{x}^{{n}} \:\:\:\:\:}{\mathrm{2}{n}+\mathrm{1}\:}\:\:\:\:{per}\:{x}\:{not}\mathrm{0} \\ $$$$/\frac{{a}_{{n}+\mathrm{1}} \left({x}\right)}{{a}_{{n}} \left({x}\right)}/=/\:\frac{{x}^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}}\:\left(\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\right)^{−\mathrm{1}} /\:\:=/\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}{x}/\:\:=\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}/{x}/ \\ $$$${and}\:{lim}_{{n}−>\propto} \:\:/\:\frac{{a}_{{n}+\mathrm{1}} \left({x}\right)}{{a}_{{n}\left({x}\right)} }/=\:/{x}/\Rightarrow\:\:{if}\:\:/{x}/<\mathrm{1}\:{the}\:{serie}\:{is}\:{convergent} \\ $$$${if}\:/{x}/>\mathrm{1}\:{the}\:{serie}\:{diverge}\:\:{if}\:{x}=\mathrm{1}\:{also}\:{the}\:{serie}\:{diverge} \\ $$$${if}\:{x}=−\mathrm{1}\:\:\:\:\sum_{{n}\geqslant\mathrm{0}} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{is}\:{convergent}\:{because}\:{its}\:{a}\:{alterne}\:{serie} \\ $$$${et}\:{S}\left({x}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto\:} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{the}\:{sum}\:{for}\:/{x}/<\mathrm{1} \\ $$$${case}\mathrm{1}\:\:\:\:\mathrm{0}<{x}<\mathrm{1}\:\:\:\:\:{S}\left({x}\right)\:\:=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(\sqrt{{x}}\right)^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\:=\:\frac{\mathrm{1}}{\sqrt{{x}}}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(\sqrt{{x}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\:\:\frac{\mathrm{1}}{\sqrt{{x}}}\:\varphi\left(\sqrt{{x}}\right){with}\:\:\varphi\left({t}\right)\:\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:\:\:{and}\:/{t}/<\mathrm{1} \\ $$$$\partial\varphi/\partial{t}\:\:=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:{t}^{\mathrm{2}{n}} \:\:\:=\:\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow\:\:\varphi\left({t}\right)\:=\int\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+\lambda \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}/\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}/+\lambda\:\:\:\:\:\:\:\lambda=\varphi\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\:\:{S}\left({x}\right)=\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\:\right) \\ $$$${case}\mathrm{2}\:\:\:\:\:\:−\mathrm{1}<{x}<\mathrm{0}\:\:\:\:\:{S}\left({x}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto\:} \:\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{−{x}}\right)^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\sqrt{−{x}}}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{−{x}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}=\:\frac{\mathrm{1}}{\sqrt{−{x}}}\psi\left(\sqrt{−{x}}\right)\:\:\:{with} \\ $$$$\psi\left({t}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:\:\:{and}\:\:/{t}/<\mathrm{1} \\ $$$$\partial\psi/\partial{t}\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} =\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−{t}^{\mathrm{2}} \right)^{{n}} =\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\psi\left({t}\right)=\:\int\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:+\kappa\:\:=\:\:{arctant}\:+\kappa\:\:\:\:\:\:\:{k}=\psi\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow \\ $$$${S}\left({x}\right)=\:\frac{{artan}\left(\sqrt{−{x}}\right)}{\sqrt{−{x}}}\:\:. \\ $$$${value}\:{of}\:{S}=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\:\:\:{we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\:{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\right)\:{if}\:\mathrm{0}{x}<\mathrm{1} \\ $$$${we}\:{take}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\:\:\:\:\:\:{S}=\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}{ln}\left(\:\:\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}{\mathrm{1}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}\right) \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{−\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$ \\ $$

Commented by prakash jain last updated on 22/Dec/17

Thanks

Terms of Service

Privacy Policy

Contact: info@tinkutara.com