
Question Number 26324 by ajfour last updated on 24/Dec/17

Commented by ajfour last updated on 24/Dec/17
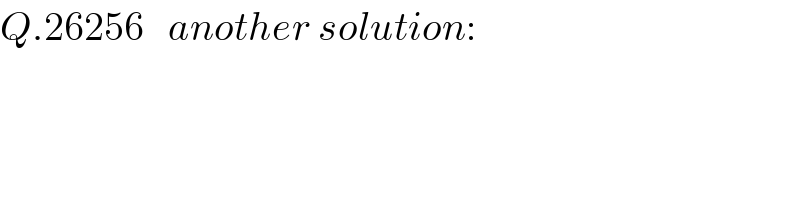
$${Q}.\mathrm{26256}\:\:\:{another}\:{solution}: \\ $$
Commented by mrW1 last updated on 24/Dec/17
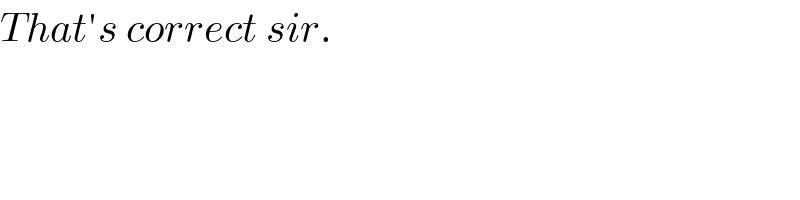
$${That}'{s}\:{correct}\:{sir}. \\ $$
Commented by ajfour last updated on 24/Dec/17

$${thanks}\:{sir},\:{but}\:{see}\:{if}\:{you}\:{can} \\ $$$${comment}\:{the}\:{same}\:{to}\:{my} \\ $$$${solution}\:{of}\:{the}\:{rotated}\:{parabola} \\ $$$${question}\:\left({that}\:{i}'{ve}\:{posted}\:{here}\right). \\ $$
Answered by ajfour last updated on 24/Dec/17

Commented by ajfour last updated on 24/Dec/17
![v=A(u−a)^2 (h,k)≡(a,0) , θ=60° after rotation eq. of parabola: As v=k+(y−k)cos θ−(x−h)sin θ u=h+(x−h)cos θ−(y−k)sin θ (y/2)−(((√3)(x−a))/2)=A[(((x−a))/2)−((y(√3))/2)]^2 it passes through origin, so ((a(√3))/2)=A((a^2 /4)) ⇒ A=((2(√3))/a) so eq. of parabola (red one) is y=(√3)(x−a)+((√3)/a)(x−a+y(√3))^2 and for blue one, θ=−60° , h=−a y=−(√3)(x+a)+((√3)/a)(x+a−y(√3))^2 For intersection points i subtract 0=+2(√3)x+((√3)/a)(2x)(−2a+2(√3)y) ⇒ x=0 or if x≠0 then y(√3)−a=−(a/2) ⇒ y_P =y_R =(a/(2(√3))) for x_P ,x_R we substitute in eq. of red parabola y=(a/(2(√3))) ⇒ (a^2 /6)=ax−a^2 +(x−(a/2))^2 or x^2 =(a^2 /6)+a^2 −(a^2 /4) x=±(√((11)/(12))) a And for x=0 we get y=−a(√3)+((√3)/a)(y(√3)−a)^2 y=−a(√3)+((3(√3)y^2 )/a)−6y+a(√3) or y(3(√3)y−7a)=0 ⇒ y_Q =((7a)/(3(√3))) so points of intersection are O(0,0) , Q(0, ((7a)/(3(√3)))) P ((√((11)/(12))) a , (a/(2(√3)))) , R (−(√((11)/(12))) a, (a/(2(√3)))) .](Q26332.png)
$${v}={A}\left({u}−{a}\right)^{\mathrm{2}} \:\:\:\left({h},{k}\right)\equiv\left({a},\mathrm{0}\right)\:,\:\theta=\mathrm{60}° \\ $$$${after}\:{rotation}\:{eq}.\:{of}\:{parabola}: \\ $$$${As}\:\:{v}={k}+\left({y}−{k}\right)\mathrm{cos}\:\theta−\left({x}−{h}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:{u}={h}+\left({x}−{h}\right)\mathrm{cos}\:\theta−\left({y}−{k}\right)\mathrm{sin}\:\theta \\ $$$$\frac{{y}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\left({x}−{a}\right)}{\mathrm{2}}={A}\left[\frac{\left({x}−{a}\right)}{\mathrm{2}}−\frac{{y}\sqrt{\mathrm{3}}}{\mathrm{2}}\right]^{\mathrm{2}} \\ $$$${it}\:{passes}\:{through}\:{origin},\:{so} \\ $$$$\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}={A}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right)\:\:\Rightarrow\:\:{A}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{{a}} \\ $$$${so}\:{eq}.\:{of}\:{parabola}\:\left({red}\:{one}\right)\:{is} \\ $$$$\boldsymbol{{y}}=\sqrt{\mathrm{3}}\left(\boldsymbol{{x}}−\boldsymbol{{a}}\right)+\frac{\sqrt{\mathrm{3}}}{\boldsymbol{{a}}}\left(\boldsymbol{{x}}−\boldsymbol{{a}}+\boldsymbol{{y}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${and}\:{for}\:\:{blue}\:{one},\:\theta=−\mathrm{60}°\:,\:{h}=−{a} \\ $$$$\boldsymbol{{y}}=−\sqrt{\mathrm{3}}\left(\boldsymbol{{x}}+\boldsymbol{{a}}\right)+\frac{\sqrt{\mathrm{3}}}{\boldsymbol{{a}}}\left(\boldsymbol{{x}}+\boldsymbol{{a}}−\boldsymbol{{y}}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${For}\:{intersection}\:{points}\:{i}\:{subtract} \\ $$$$\mathrm{0}=+\mathrm{2}\sqrt{\mathrm{3}}{x}+\frac{\sqrt{\mathrm{3}}}{{a}}\left(\mathrm{2}{x}\right)\left(−\mathrm{2}{a}+\mathrm{2}\sqrt{\mathrm{3}}{y}\right) \\ $$$$\Rightarrow\:{x}=\mathrm{0}\:\:{or}\:{if}\:{x}\neq\mathrm{0}\:\:{then} \\ $$$${y}\sqrt{\mathrm{3}}−{a}=−\frac{{a}}{\mathrm{2}}\:\:\:\Rightarrow\:\:{y}_{{P}} ={y}_{{R}} =\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\: \\ $$$${for}\:{x}_{{P}} \:,{x}_{{R}} \:\:{we}\:{substitute}\:{in}\:{eq}.\:{of}\: \\ $$$${red}\:\:{parabola}\:{y}=\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\frac{{a}^{\mathrm{2}} }{\mathrm{6}}={ax}−{a}^{\mathrm{2}} +\left({x}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${or}\:\:\:{x}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{6}}+{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\:\:\:{x}=\pm\sqrt{\frac{\mathrm{11}}{\mathrm{12}}}\:{a}\:\: \\ $$$${And}\:{for}\:\:{x}=\mathrm{0}\:\:{we}\:{get} \\ $$$${y}=−{a}\sqrt{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}}{{a}}\left({y}\sqrt{\mathrm{3}}−{a}\right)^{\mathrm{2}} \\ $$$${y}=−{a}\sqrt{\mathrm{3}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}{y}^{\mathrm{2}} }{{a}}−\mathrm{6}{y}+{a}\sqrt{\mathrm{3}} \\ $$$${or}\:\:{y}\left(\mathrm{3}\sqrt{\mathrm{3}}{y}−\mathrm{7}{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{y}}_{\boldsymbol{{Q}}} =\frac{\mathrm{7}{a}}{\mathrm{3}\sqrt{\mathrm{3}}}\: \\ $$$${so}\:{points}\:{of}\:{intersection}\:{are} \\ $$$${O}\left(\mathrm{0},\mathrm{0}\right)\:\:,\:\:\:{Q}\left(\mathrm{0},\:\frac{\mathrm{7}{a}}{\mathrm{3}\sqrt{\mathrm{3}}}\right) \\ $$$${P}\:\left(\sqrt{\frac{\mathrm{11}}{\mathrm{12}}}\:{a}\:,\:\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)\:,\:{R}\:\left(−\sqrt{\frac{\mathrm{11}}{\mathrm{12}}}\:{a},\:\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)\:. \\ $$
Commented by mrW1 last updated on 24/Dec/17

$${Very}\:{nice}\:{sir}! \\ $$
