Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 26397 by abdo imad last updated on 25/Dec/17

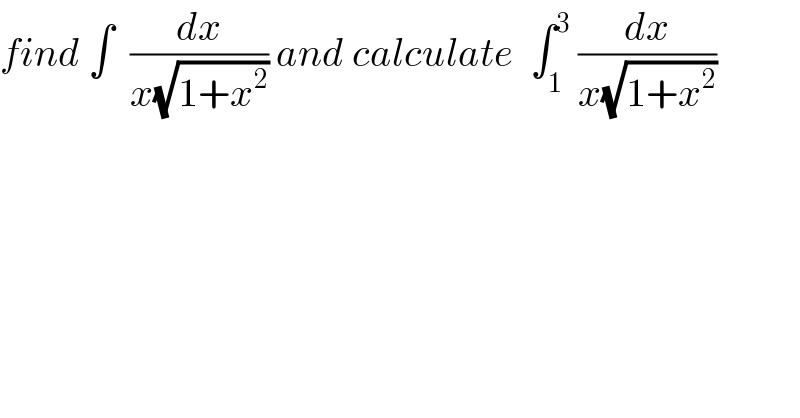
find ∫ (dx/(x(√(1+x^2 )))) and calculate ∫_1 ^3 (dx/(x(√(1+x^2 ))))

$${find}\:\int\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{and}\:{calculate}\:\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$

Commented by abdo imad last updated on 26/Dec/17

let use the changement x=tanθ ∫ (dx/(x (√(1+x^2 ))))= ∫ (((1+tan^2 θ)dθ)/(tanθ (√(1+tan^2 ))))dθ= ∫ ((√(1+tan^2 θ))/(tanθ))dθ = ∫ (1/(cosθ tanθ))dθ= ∫ (dθ/(sinθ )) and by thechangement tan(θ/2)=t I= ∫ ((2dt)/(1+t^2 ))(((2t)/(1+t^2 )))^(−1) = ∫dt/t=ln/t/=ln/tan(((arctanx)/2) )/ ln ⇒ ∫ (dx/(x(√(1+x^2 ))))=ln/tan(((arctanx)/2) )/ +k ∫_1 ^3 (dx/(x(√(1+x^2 )))) = ln/tan(2^(−1) arctan3) /−ln/tan(2^(−1) arctan1)/ ==ln/tan(((arctan3)/2))/ −ln/tan((π/8))/ .

$${let}\:{use}\:{the}\:{changement}\:{x}={tan}\theta \\ $$$$\int\:\:\frac{{dx}}{{x}\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\:\:\:\:\int\:\:\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{{tan}\theta\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} }}{d}\theta=\:\int\:\frac{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{{tan}\theta}{d}\theta \\ $$$$=\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{{cos}\theta\:{tan}\theta}{d}\theta=\:\:\int\:\:\frac{{d}\theta}{{sin}\theta\:}\:\:\:{and}\:{by}\:{thechangement}\:{tan}\left(\theta/\mathrm{2}\right)={t} \\ $$$${I}=\:\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{−\mathrm{1}} \:\:=\:\int{dt}/{t}={ln}/{t}/={ln}/{tan}\left(\frac{{arctanx}}{\mathrm{2}}\:\right)/\:{ln} \\ $$$$\Rightarrow\:\:\:\int\:\:\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}={ln}/{tan}\left(\frac{{arctanx}}{\mathrm{2}}\:\right)/\:+{k} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:=\:{ln}/{tan}\left(\mathrm{2}^{−\mathrm{1}} {arctan}\mathrm{3}\right)\:/−{ln}/{tan}\left(\mathrm{2}^{−\mathrm{1}} {arctan}\mathrm{1}\right)/ \\ $$$$=={ln}/{tan}\left(\frac{{arctan}\mathrm{3}}{\mathrm{2}}\right)/\:\:−{ln}/{tan}\left(\frac{\pi}{\mathrm{8}}\right)/\:. \\ $$

Answered by $@ty@m last updated on 25/Dec/17

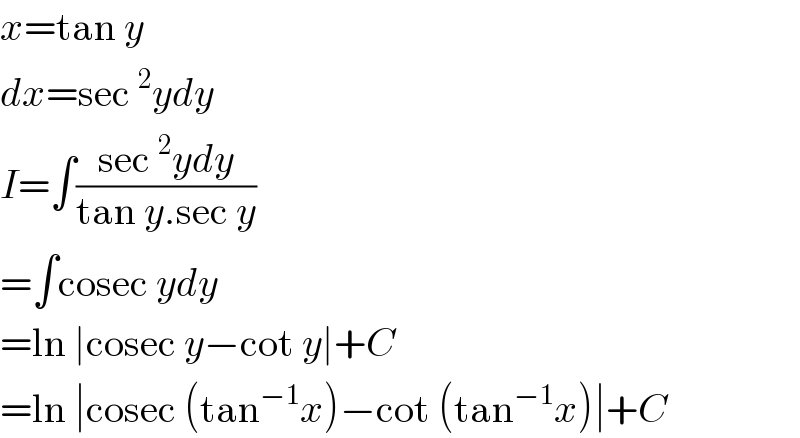
x=tan y dx=sec^2 ydy I=∫((sec^2 ydy)/(tan y.sec y)) =∫cosec ydy =ln ∣cosec y−cot y∣+C =ln ∣cosec (tan^(−1) x)−cot (tan^(−1) x)∣+C

$${x}=\mathrm{tan}\:{y} \\ $$$${dx}=\mathrm{sec}\:^{\mathrm{2}} {ydy} \\ $$$${I}=\int\frac{\mathrm{sec}\:^{\mathrm{2}} {ydy}}{\mathrm{tan}\:{y}.\mathrm{sec}\:{y}} \\ $$$$=\int\mathrm{cosec}\:{ydy} \\ $$$$=\mathrm{ln}\:\mid\mathrm{cosec}\:{y}−\mathrm{cot}\:{y}\mid+{C} \\ $$$$=\mathrm{ln}\:\mid\mathrm{cosec}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)−\mathrm{cot}\:\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)\mid+{C} \\ $$

Answered by $@ty@m last updated on 25/Dec/17

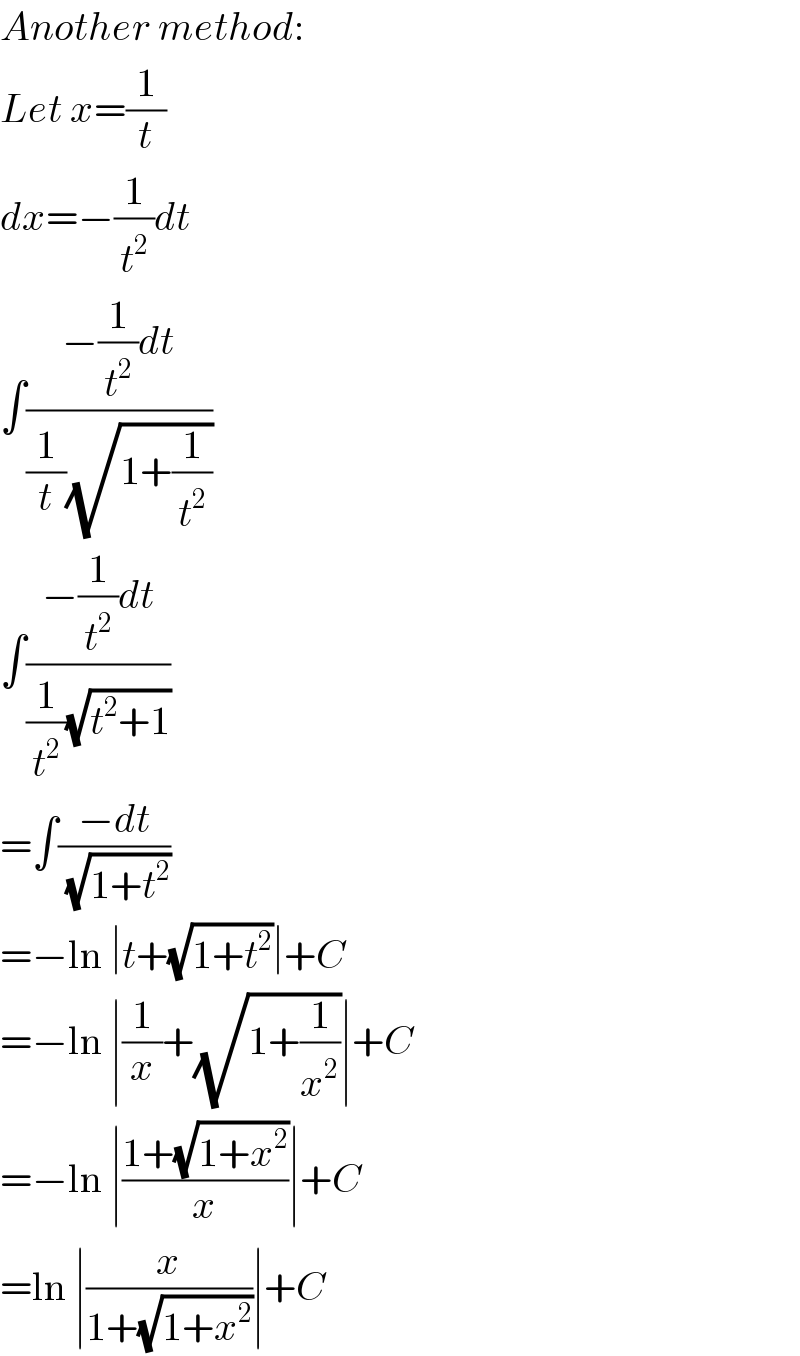
Another method: Let x=(1/t) dx=−(1/t^2 )dt ∫((−(1/t^2 )dt)/((1/t)(√(1+(1/t^2 ))))) ∫((−(1/t^2 )dt)/((1/t^2 )(√(t^2 +1)))) =∫((−dt)/(√(1+t^2 ))) =−ln ∣t+(√(1+t^2 ))∣+C =−ln ∣(1/x)+(√(1+(1/x^2 )))∣+C =−ln ∣((1+(√(1+x^2 )))/x)∣+C =ln ∣(x/(1+(√(1+x^2 ))))∣+C

$${Another}\:{method}: \\ $$$${Let}\:{x}=\frac{\mathrm{1}}{{t}} \\ $$$${dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt}}{\frac{\mathrm{1}}{{t}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}} \\ $$$$\int\frac{−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt}}{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$=\int\frac{−{dt}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$=−\mathrm{ln}\:\mid{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\mid+{C} \\ $$$$=−\mathrm{ln}\:\mid\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\mid+{C} \\ $$$$=−\mathrm{ln}\:\mid\frac{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\mid+{C} \\ $$$$=\mathrm{ln}\:\mid\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com