Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 26398 by abdo imad last updated on 25/Dec/17

find the value of ∫∫_D x^2 y dxdy on the domain D={(x.y)∈R^2 / x^2 +y^2 −2x≤0 and y≥0}

$${find}\:{the}\:{value}\:{of}\:\:\int\int_{{D}} \:{x}^{\mathrm{2}} {y}\:{dxdy}\:\:\:{on}\:{the}\:{domain} \\ $$$${D}=\left\{\left({x}.{y}\right)\in{R}^{\mathrm{2}} /\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−\mathrm{2}{x}\leqslant\mathrm{0}\:{and}\:{y}\geqslant\mathrm{0}\right\} \\ $$

Commented by abdo imad last updated on 25/Dec/17

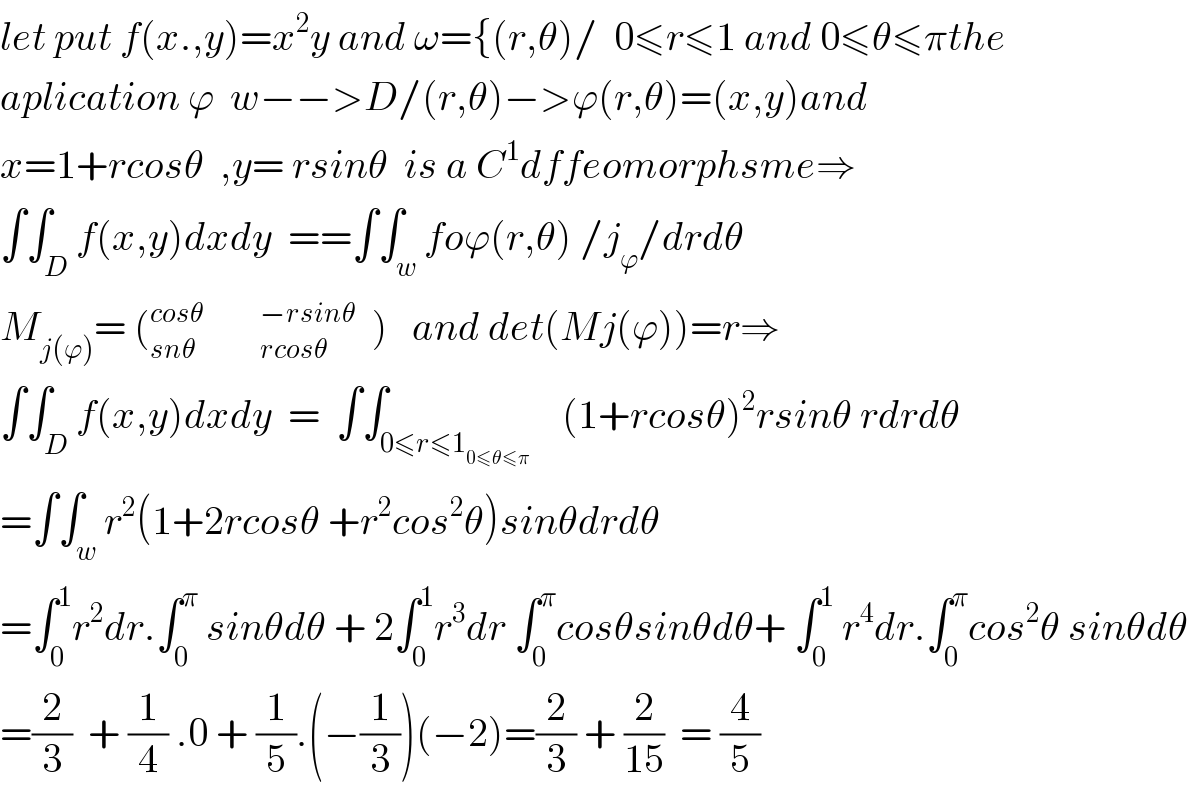
let put f(x.,y)=x^2 y and ω={(r,θ)/ 0≤r≤1 and 0≤θ≤πthe aplication ϕ w−−>D/(r,θ)−>ϕ(r,θ)=(x,y)and x=1+rcosθ ,y= rsinθ is a C^1 dffeomorphsme⇒ ∫∫_D f(x,y)dxdy ==∫∫_w foϕ(r,θ) /j_ϕ /drdθ M_(j(ϕ)) = (_(snθ rcosθ) ^(cosθ −rsinθ) ) and det(Mj(ϕ))=r⇒ ∫∫_D f(x,y)dxdy = ∫∫_(0≤r≤1_(0≤θ≤π) ) (1+rcosθ)^2 rsinθ rdrdθ =∫∫_w r^2 (1+2rcosθ +r^2 cos^2 θ)sinθdrdθ =∫_0 ^1 r^2 dr.∫_0 ^π sinθdθ + 2∫_0 ^1 r^3 dr ∫_0 ^π cosθsinθdθ+ ∫_0 ^1 r^4 dr.∫_0 ^π cos^2 θ sinθdθ =(2/3) + (1/4) .0 + (1/5).(−(1/3))(−2)=(2/3) + (2/(15)) = (4/5)

$${let}\:{put}\:{f}\left({x}.,{y}\right)={x}^{\mathrm{2}} {y}\:{and}\:\omega=\left\{\left({r},\theta\right)/\:\:\mathrm{0}\leqslant{r}\leqslant\mathrm{1}\:{and}\:\mathrm{0}\leqslant\theta\leqslant\pi{the}\right. \\ $$$${aplication}\:\varphi\:\:{w}−−>{D}/\left({r},\theta\right)−>\varphi\left({r},\theta\right)=\left({x},{y}\right){and} \\ $$$${x}=\mathrm{1}+{rcos}\theta\:\:,{y}=\:{rsin}\theta\:\:{is}\:{a}\:{C}^{\mathrm{1}} {dffeomorphsme}\Rightarrow \\ $$$$\int\int_{{D}} {f}\left({x},{y}\right){dxdy}\:\:==\int\int_{{w}} {fo}\varphi\left({r},\theta\right)\:/{j}_{\varphi} /{drd}\theta \\ $$$${M}_{{j}\left(\varphi\right)} =\:\left(_{{sn}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{rcos}\theta} ^{{cos}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{rsin}\theta} \:\:\right)\:\:\:{and}\:{det}\left({Mj}\left(\varphi\right)\right)={r}\Rightarrow \\ $$$$\int\int_{{D}} {f}\left({x},{y}\right){dxdy}\:\:=\:\:\int\int_{\mathrm{0}\leqslant{r}\leqslant\mathrm{1}_{\mathrm{0}\leqslant\theta\leqslant\pi} } \:\:\:\left(\mathrm{1}+{rcos}\theta\right)^{\mathrm{2}} {rsin}\theta\:{rdrd}\theta \\ $$$$=\int\int_{{w}} {r}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{rcos}\theta\:+{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right){sin}\theta{drd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {r}^{\mathrm{2}} {dr}.\int_{\mathrm{0}} ^{\pi} \:{sin}\theta{d}\theta\:+\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {r}^{\mathrm{3}} {dr}\:\int_{\mathrm{0}} ^{\pi} {cos}\theta{sin}\theta{d}\theta+\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{r}^{\mathrm{4}} {dr}.\int_{\mathrm{0}} ^{\pi} {cos}^{\mathrm{2}} \theta\:{sin}\theta{d}\theta \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:.\mathrm{0}\:+\:\frac{\mathrm{1}}{\mathrm{5}}.\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(−\mathrm{2}\right)=\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{2}}{\mathrm{15}}\:\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$

Commented by ajfour last updated on 25/Dec/17

Answered by kaivan.ahmadi last updated on 25/Dec/17

Commented by prakash jain last updated on 25/Dec/17

if you CamScanner app image will be cleaner https://play.google.com/store/apps/details?id=com.intsig.camscanner

Answered by ajfour last updated on 25/Dec/17

x=rcos θ , y=rsin θ , r_(max) =2cos θ_(max) dxdy=(rdr)dθ ∫∫_D (x^2 y)(dxdy) =∫_0 ^( π/2) ∫_0 ^(2cos θ_(max) ) (r^3 cos^2 θsin θ)(rdrdθ) =∫_0 ^( π/2) [∫_0 ^(2cos θ_(max) ) (r^4 dr)]cos^2 θsin θdθ =∫_0 ^( π/2) (((2cos θ)^5 cos^2 θsin θ)/5)dθ =((32)/5)×(((cos θ)^8 )/8)∣_(π/2) ^0 =(4/5) .

$${x}={r}\mathrm{cos}\:\theta\:\:,\:\:{y}={r}\mathrm{sin}\:\theta\:,\:{r}_{{max}} =\mathrm{2cos}\:\theta_{{max}} \\ $$$${dxdy}=\left({rdr}\right){d}\theta \\ $$$$\int\int_{{D}} \left({x}^{\mathrm{2}} {y}\right)\left({dxdy}\right) \\ $$$$=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{2cos}\:\theta_{{max}} } \left({r}^{\mathrm{3}} \mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:\theta\right)\left({rdrd}\theta\right) \\ $$$$=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \left[\int_{\mathrm{0}} ^{\mathrm{2cos}\:\theta_{{max}} } \left({r}^{\mathrm{4}} {dr}\right)\right]\mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:\theta{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{2cos}\:\theta\right)^{\mathrm{5}} \mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:\theta}{\mathrm{5}}{d}\theta \\ $$$$=\frac{\mathrm{32}}{\mathrm{5}}×\frac{\left(\mathrm{cos}\:\theta\right)^{\mathrm{8}} }{\mathrm{8}}\mid_{\pi/\mathrm{2}} ^{\mathrm{0}} \:=\frac{\mathrm{4}}{\mathrm{5}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com