
Question Number 26401 by abdo imad last updated on 25/Dec/17

$${find}\:{the}\:{sum}\:{of}\:\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\frac{\mathrm{1}}{{n}\:\:\mathrm{2}^{{n}} }\:\:. \\ $$
Commented by abdo imad last updated on 25/Dec/17
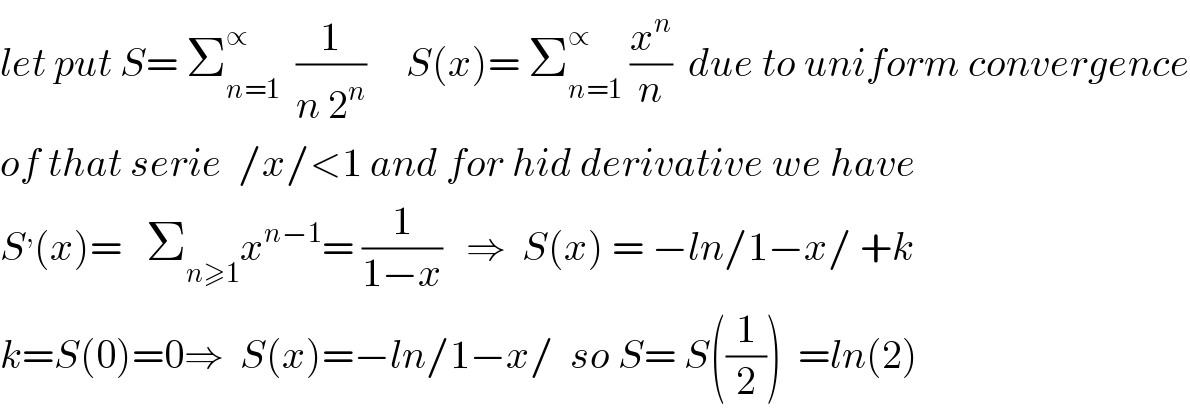
$${let}\:{put}\:{S}=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\frac{\mathrm{1}}{{n}\:\mathrm{2}^{{n}} }\:\:\:\:\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\frac{{x}^{{n}} }{{n}}\:\:{due}\:{to}\:{uniform}\:{convergence} \\ $$$${of}\:{that}\:{serie}\:\:/{x}/<\mathrm{1}\:{and}\:{for}\:{hid}\:{derivative}\:{we}\:{have} \\ $$$${S}^{,} \left({x}\right)=\:\:\:\sum_{{n}\geqslant\mathrm{1}} {x}^{{n}−\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:\Rightarrow\:\:{S}\left({x}\right)\:=\:−{ln}/\mathrm{1}−{x}/\:+{k} \\ $$$${k}={S}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\:\:{S}\left({x}\right)=−{ln}/\mathrm{1}−{x}/\:\:{so}\:{S}=\:{S}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:={ln}\left(\mathrm{2}\right) \\ $$
Answered by prakash jain last updated on 25/Dec/17
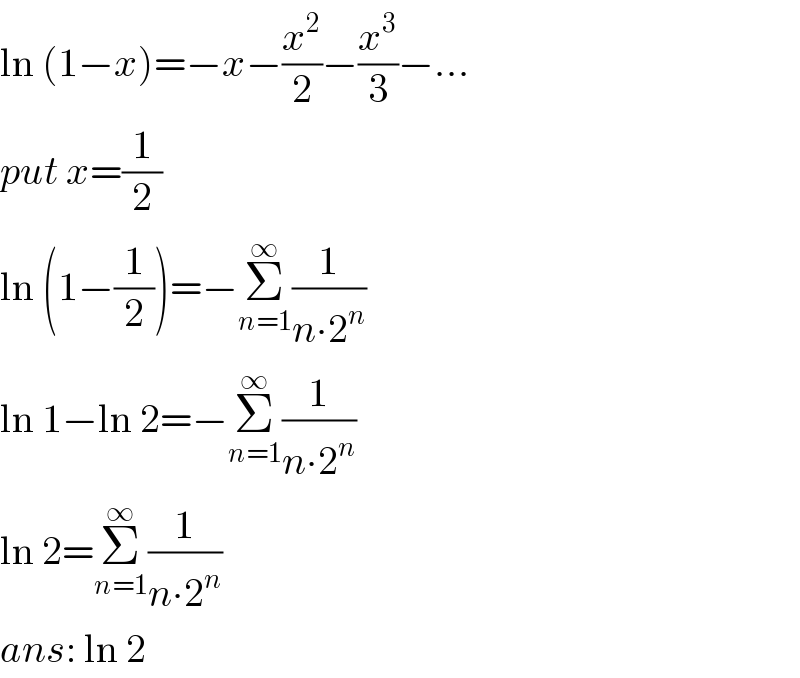
$$\mathrm{ln}\:\left(\mathrm{1}−{x}\right)=−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−... \\ $$$${put}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\centerdot\mathrm{2}^{{n}} } \\ $$$$\mathrm{ln}\:\mathrm{1}−\mathrm{ln}\:\mathrm{2}=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\centerdot\mathrm{2}^{{n}} } \\ $$$$\mathrm{ln}\:\mathrm{2}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\centerdot\mathrm{2}^{{n}} } \\ $$$${ans}:\:\mathrm{ln}\:\mathrm{2} \\ $$
