
Question and Answers Forum
Question Number 26411 by Tinkutara last updated on 25/Dec/17
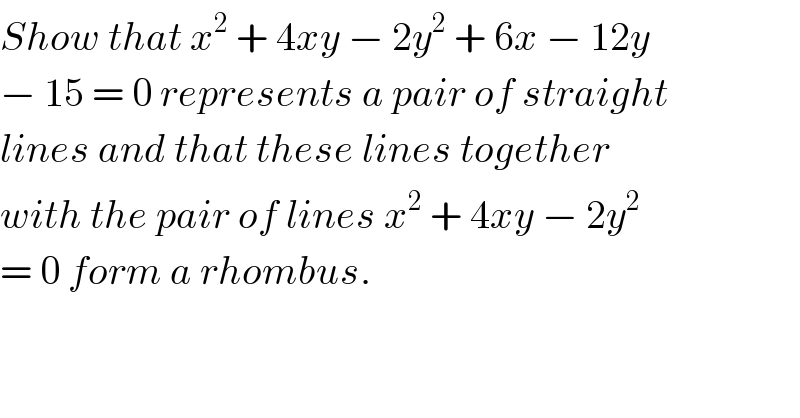
Answered by ajfour last updated on 25/Dec/17
![x^2 +4xy−2y^2 +6x−12y−15=0 determinant ((a,h,g),(h,b,f),(g,f,( c)))= determinant ((1,2,3),(2,(−2),(−6)),(3,(−6),(−15))) =−6+24−18 =0 hence pair of straight lines. If both pair of lines having same two slopes, have a common angular bisector , then they form a rhombus. Here as the other pair passes through origin, we can prove this by showing origin is equidistant from the each line of the first pair. ⇒ (c_1 /(√(1+m_1 ^2 )))=(c_2 /(√(1+m_2 ^2 ))) or c_1 ^2 (1+m_2 ^2 )=c_2 ^2 (1+m_1 ^2 ) ..(i) (y−m_1 x−c_1 )(y−m_2 x−c_2 )=0 c_1 c_2 =((−15)/(−2)) =((15)/2) ; they are roots of z^2 +6z+((15)/2)=0 c_1 ,c_2 =((−6±(√(36−30)))/2)=−3±((√6)/2) m_1 m_2 =(a/b)=−(1/2) , m_1 +m_2 =−((2h)/b)=2 ; ⇒ roots of z^2 −2z−(1/2)=0 m_1 , m_2 =((2±(√(4+2)))/2) =1±((√6)/2) Also m_1 c_2 +m_2 c_1 =((2g)/b) =(6/(−2))=−3 (1+((√6)/2))(−3−((√6)/2))+(1−((√6)/2))(−3+((√6)/2)) =−3−((√6)/2)−((3(√6))/2)−(3/2)−3+((√6)/2)+((3(√6))/2)−(3/2) =−9 , so (1+((√6)/2))(−3+((√6)/2))+(1−((√6)/2))(−3−((√6)/2)) =−(3/2)−(√6) −(3/2)+(√6) =−3 ....(ii) hence if m_1 =1−((√6)/2) , c_2 =−3−((√6)/2) eq. of angular bisector of first pair of lines are thus ((y−m_1 x−c_1 )/(√(1+m_1 ^2 )))=±((y−m_2 x−c_2 )/(√(1+m_2 ^2 ))) as to form a rhombus one bisector line must pass through origin , so c_1 (√(1+m_2 ^2 )) =c_2 (√(1+m_1 ^2 )) as c_1 c_2 > 0 ⇒ c_1 ^2 −c_2 ^2 =m_1 ^2 c_2 ^2 −m_2 ^2 c_1 ^2 (c_1 +c_2 )(c_1 −c_2 )=(m_1 c_2 +m_2 c_1 )× (m_1 c_2 −m_2 c_1 ) l.h.s. =(−6)((√6)) =−6(√6) r.h.s.=(−3)(2(√6))=−6(√6) [see (ii)] hence the lines form a rhombus.](Q26426.png)
Commented by Tinkutara last updated on 25/Dec/17
Thank you Sir!
| ||
Question and Answers Forum | ||
Question Number 26411 by Tinkutara last updated on 25/Dec/17 | ||
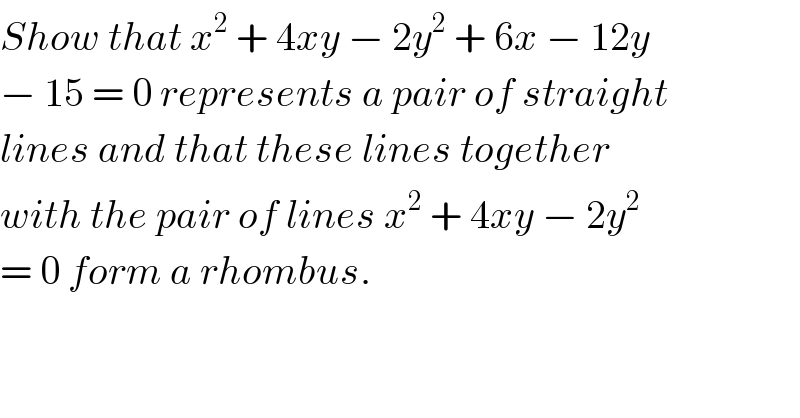 | ||
Answered by ajfour last updated on 25/Dec/17 | ||
![x^2 +4xy−2y^2 +6x−12y−15=0 determinant ((a,h,g),(h,b,f),(g,f,( c)))= determinant ((1,2,3),(2,(−2),(−6)),(3,(−6),(−15))) =−6+24−18 =0 hence pair of straight lines. If both pair of lines having same two slopes, have a common angular bisector , then they form a rhombus. Here as the other pair passes through origin, we can prove this by showing origin is equidistant from the each line of the first pair. ⇒ (c_1 /(√(1+m_1 ^2 )))=(c_2 /(√(1+m_2 ^2 ))) or c_1 ^2 (1+m_2 ^2 )=c_2 ^2 (1+m_1 ^2 ) ..(i) (y−m_1 x−c_1 )(y−m_2 x−c_2 )=0 c_1 c_2 =((−15)/(−2)) =((15)/2) ; they are roots of z^2 +6z+((15)/2)=0 c_1 ,c_2 =((−6±(√(36−30)))/2)=−3±((√6)/2) m_1 m_2 =(a/b)=−(1/2) , m_1 +m_2 =−((2h)/b)=2 ; ⇒ roots of z^2 −2z−(1/2)=0 m_1 , m_2 =((2±(√(4+2)))/2) =1±((√6)/2) Also m_1 c_2 +m_2 c_1 =((2g)/b) =(6/(−2))=−3 (1+((√6)/2))(−3−((√6)/2))+(1−((√6)/2))(−3+((√6)/2)) =−3−((√6)/2)−((3(√6))/2)−(3/2)−3+((√6)/2)+((3(√6))/2)−(3/2) =−9 , so (1+((√6)/2))(−3+((√6)/2))+(1−((√6)/2))(−3−((√6)/2)) =−(3/2)−(√6) −(3/2)+(√6) =−3 ....(ii) hence if m_1 =1−((√6)/2) , c_2 =−3−((√6)/2) eq. of angular bisector of first pair of lines are thus ((y−m_1 x−c_1 )/(√(1+m_1 ^2 )))=±((y−m_2 x−c_2 )/(√(1+m_2 ^2 ))) as to form a rhombus one bisector line must pass through origin , so c_1 (√(1+m_2 ^2 )) =c_2 (√(1+m_1 ^2 )) as c_1 c_2 > 0 ⇒ c_1 ^2 −c_2 ^2 =m_1 ^2 c_2 ^2 −m_2 ^2 c_1 ^2 (c_1 +c_2 )(c_1 −c_2 )=(m_1 c_2 +m_2 c_1 )× (m_1 c_2 −m_2 c_1 ) l.h.s. =(−6)((√6)) =−6(√6) r.h.s.=(−3)(2(√6))=−6(√6) [see (ii)] hence the lines form a rhombus.](Q26426.png) | ||
| ||
Commented by Tinkutara last updated on 25/Dec/17 | ||
Thank you Sir! | ||