
Question Number 26566 by abdo imad last updated on 26/Dec/17
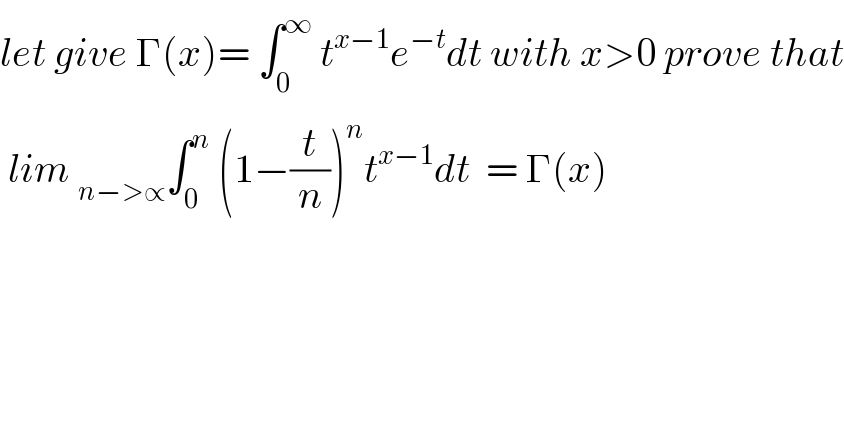
$${let}\:{give}\:\Gamma\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:{with}\:{x}>\mathrm{0}\:{prove}\:{that} \\ $$ $$\:{lim}\:_{{n}−>\propto} \int_{\mathrm{0}} ^{{n}} \:\left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} {t}^{{x}−\mathrm{1}} {dt}\:\:=\:\Gamma\left({x}\right) \\ $$
Commented byabdo imad last updated on 28/Dec/17
![let put A_n = ∫_0 ^n (1−(t/n))^n t^(x−1) dt A_n = ∫_R f_n (t)dt where the sequence f_n = (1−(t/n))^n t^(x−1) χ_([0,n]) (t)we have f_n −>_(c.s) f(t)= e^(−t) t^(x−1) on [0,∝[ but /f_n /≤ ρ(t)= e^(−t ) t^(x−1 ) χ_([0,α) by theoreme of vonvergence domine ∫_R f_n (t)dt_(n−∝) −−>∫_0 ^∞ e^(−t) t^(x−1) dx=Γ(x)](Q26678.png)
$${let}\:{put}\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{{n}} \left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} \:{t}^{{x}−\mathrm{1}} {dt} \\ $$ $${A}_{{n}} \:\:=\:\:\int_{\mathbb{R}} {f}_{{n}} \left({t}\right){dt}\:\:\:{where}\:{the}\:{sequence} \\ $$ $${f}_{{n}} =\:\:\left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} \:{t}^{{x}−\mathrm{1}} \:\chi_{\left[\mathrm{0},{n}\right]} \left({t}\right){we}\:{have} \\ $$ $${f}_{{n}} −>_{{c}.{s}} {f}\left({t}\right)=\:{e}^{−{t}} \:{t}^{{x}−\mathrm{1}} {on}\:\left[\mathrm{0},\propto\left[\right.\right. \\ $$ $${but}\:/{f}_{{n}} \:/\leqslant\:\rho\left({t}\right)=\:{e}^{−{t}\:} \:{t}^{{x}−\mathrm{1}\:} \chi_{\left[\mathrm{0},\alpha\right.} \:{by}\:{theoreme} \\ $$ $${of}\:{vonvergence}\:{domine} \\ $$ $$\int_{\mathbb{R}} {f}_{{n}} \:\left({t}\right){dt}_{{n}−\propto} −−>\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \:{t}^{{x}−\mathrm{1}} {dx}=\Gamma\left({x}\right) \\ $$
