
Question Number 26570 by abdo imad last updated on 26/Dec/17
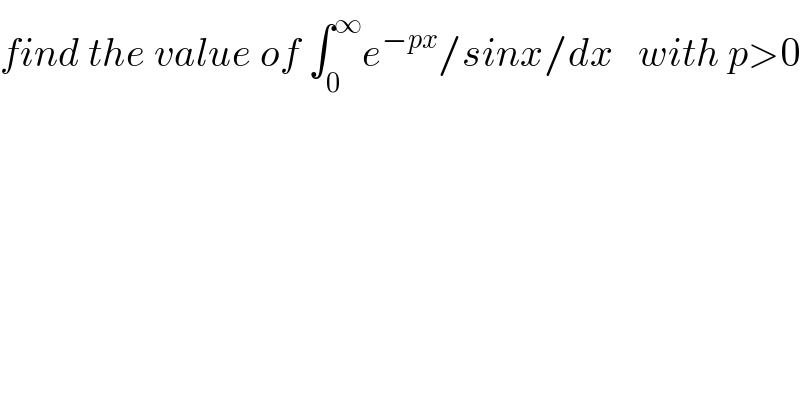
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{px}} /{sinx}/{dx}\:\:\:{with}\:{p}>\mathrm{0} \\ $$
Commented byabdo imad last updated on 02/Jan/18
![let put I= ∫_0 ^∝ e^(−px) /sinx/dx I= lim_(n−>∝) ∫_0 ^(nπ) e^(−px) /sinx/dx but ∫_0 ^(nπ) e^(−px) /sinx/dx= Σ_(k=0) ^(n−1) ∫_(kπ) ^((k+1)π) e^(−px) /sinx/dx = Σ_(k=0) ^(n−1) ∫_0 ^π e^(−p(kπ+t)) /sin(kπ+t)/dt ( we do the changement x=kπ +t) = Σ_(k=0) ^(n−1) e^(−pkπ) ∫_0 ^π e^(−pt) sint dt = Σ_(k=0) ^(n−1) (e^(−pπ) )^k ∫_0 ^π e^(−pt) sintdt = ((1− e^(−npπ) )/(1− e^(−pπ) )) ∫_0 ^π e^(−pt) sintdt but ∫_0 ^π e^(−pt) sintdt = Im( ∫_0 ^π e^((i−p)t) dt ) =Im( [ (1/(i−p)) e^((i−p)t) ]_0 ^(π ) = ((1+e^(−pπ) )/(1+p^2 )) I= (1/(1−e^(−pπ) )) . ((1+ e^(−pπ) )/(1+p^2 )) = ((1+ e^(−pπ) )/((1+p^2 )(1−e^(−pπ) ))) .](Q27176.png)
$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\propto} \:{e}^{−{px}} /{sinx}/{dx} \\ $$ $${I}=\:{lim}_{{n}−>\propto} \:\int_{\mathrm{0}} ^{{n}\pi} \:{e}^{−{px}} /{sinx}/{dx}\:\:{but}\: \\ $$ $$\int_{\mathrm{0}} ^{{n}\pi} {e}^{−{px}} /{sinx}/{dx}=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{{k}\pi} ^{\left({k}+\mathrm{1}\right)\pi} \:{e}^{−{px}} /{sinx}/{dx} \\ $$ $$=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\pi} \:\:{e}^{−{p}\left({k}\pi+{t}\right)} /{sin}\left({k}\pi+{t}\right)/{dt}\:\left(\:{we}\:{do}\:{the}\:{changement}\:{x}={k}\pi\:+{t}\right) \\ $$ $$=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{e}^{−{pk}\pi} \:\:\int_{\mathrm{0}} ^{\pi} \:{e}^{−{pt}} {sint}\:{dt}\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left({e}^{−{p}\pi} \right)^{{k}} \:\int_{\mathrm{0}} ^{\pi} \:{e}^{−{pt}} \:{sintdt} \\ $$ $$=\:\frac{\mathrm{1}−\:\:{e}^{−{np}\pi} }{\mathrm{1}−\:{e}^{−{p}\pi} }\:\int_{\mathrm{0}} ^{\pi} \:{e}^{−{pt}} {sintdt}\:\:\:{but} \\ $$ $$\:\int_{\mathrm{0}} ^{\pi} \:{e}^{−{pt}} {sintdt}\:=\:{Im}\left(\:\int_{\mathrm{0}} ^{\pi} \:{e}^{\left({i}−{p}\right){t}} {dt}\:\right) \\ $$ $$\: \\ $$ $$\:\:\: \\ $$ $$={Im}\left(\:\:\left[\:\frac{\mathrm{1}}{{i}−{p}}\:{e}^{\left({i}−{p}\right){t}} \:\right]_{\mathrm{0}} ^{\pi\:} =\:\frac{\mathrm{1}+{e}^{−{p}\pi} }{\mathrm{1}+{p}^{\mathrm{2}} }\right. \\ $$ $${I}=\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{p}\pi} }\:.\:\frac{\mathrm{1}+\:{e}^{−{p}\pi} }{\mathrm{1}+{p}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}+\:{e}^{−{p}\pi} }{\left(\mathrm{1}+{p}^{\mathrm{2}} \right)\left(\mathrm{1}−{e}^{−{p}\pi} \right)}\:. \\ $$
