
Question Number 26626 by ajfour last updated on 27/Dec/17

Answered by mrW1 last updated on 28/Dec/17
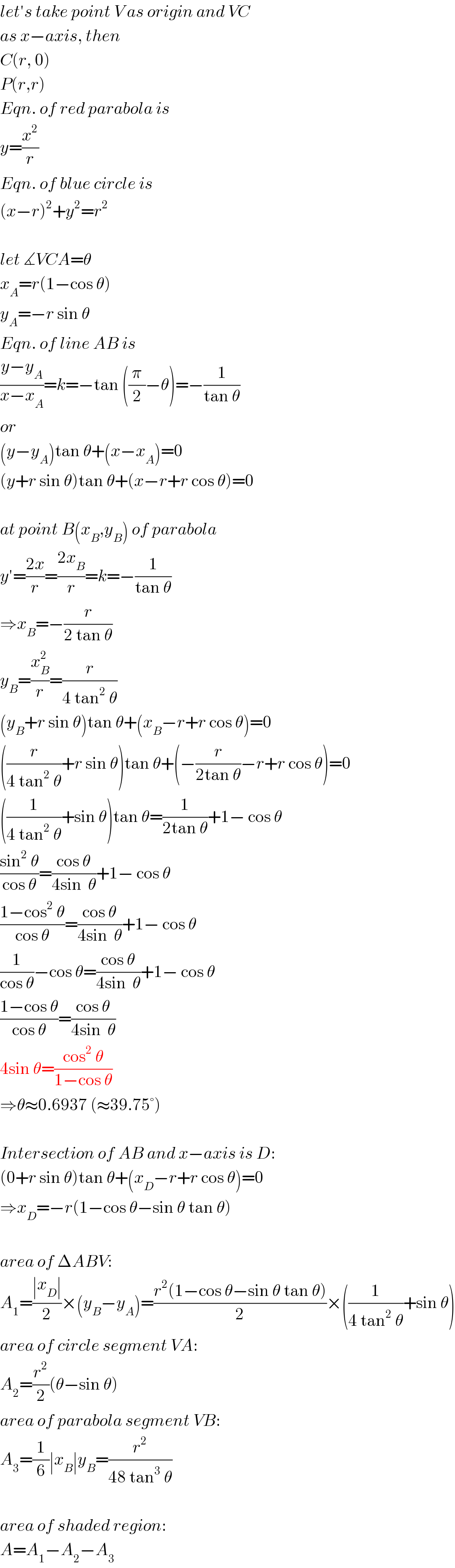
$${let}'{s}\:{take}\:{point}\:{V}\:{as}\:{origin}\:{and}\:{VC} \\ $$$${as}\:{x}−{axis},\:{then} \\ $$$${C}\left({r},\:\mathrm{0}\right) \\ $$$${P}\left({r},{r}\right) \\ $$$${Eqn}.\:{of}\:{red}\:{parabola}\:{is}\: \\ $$$${y}=\frac{{x}^{\mathrm{2}} }{{r}} \\ $$$${Eqn}.\:{of}\:{blue}\:{circle}\:{is} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$${let}\:\measuredangle{VCA}=\theta \\ $$$${x}_{{A}} ={r}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${y}_{{A}} =−{r}\:\mathrm{sin}\:\theta \\ $$$${Eqn}.\:{of}\:{line}\:{AB}\:{is} \\ $$$$\frac{{y}−{y}_{{A}} }{{x}−{x}_{{A}} }={k}=−\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)=−\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$${or} \\ $$$$\left({y}−{y}_{{A}} \right)\mathrm{tan}\:\theta+\left({x}−{x}_{{A}} \right)=\mathrm{0} \\ $$$$\left({y}+{r}\:\mathrm{sin}\:\theta\right)\mathrm{tan}\:\theta+\left({x}−{r}+{r}\:\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$ \\ $$$${at}\:{point}\:{B}\left({x}_{{B}} ,{y}_{{B}} \right)\:{of}\:{parabola} \\ $$$${y}'=\frac{\mathrm{2}{x}}{{r}}=\frac{\mathrm{2}{x}_{{B}} }{{r}}={k}=−\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow{x}_{{B}} =−\frac{{r}}{\mathrm{2}\:\mathrm{tan}\:\theta} \\ $$$${y}_{{B}} =\frac{{x}_{{B}} ^{\mathrm{2}} }{{r}}=\frac{{r}}{\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$$\left({y}_{{B}} +{r}\:\mathrm{sin}\:\theta\right)\mathrm{tan}\:\theta+\left({x}_{{B}} −{r}+{r}\:\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\left(\frac{{r}}{\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\theta}+{r}\:\mathrm{sin}\:\theta\right)\mathrm{tan}\:\theta+\left(−\frac{{r}}{\mathrm{2tan}\:\theta}−{r}+{r}\:\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\theta}+\mathrm{sin}\:\theta\right)\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{2tan}\:\theta}+\mathrm{1}−\:\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{cos}\:\theta}=\frac{\mathrm{cos}\:\theta}{\mathrm{4sin}\:\:\theta}+\mathrm{1}−\:\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{cos}\:\theta}=\frac{\mathrm{cos}\:\theta}{\mathrm{4sin}\:\:\theta}+\mathrm{1}−\:\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}\:\theta}−\mathrm{cos}\:\theta=\frac{\mathrm{cos}\:\theta}{\mathrm{4sin}\:\:\theta}+\mathrm{1}−\:\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{cos}\:\theta}=\frac{\mathrm{cos}\:\theta}{\mathrm{4sin}\:\:\theta} \\ $$$$\mathrm{4sin}\:\theta=\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{1}−\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\theta\approx\mathrm{0}.\mathrm{6937}\:\left(\approx\mathrm{39}.\mathrm{75}°\right) \\ $$$$ \\ $$$${Intersection}\:{of}\:{AB}\:{and}\:{x}−{axis}\:{is}\:{D}: \\ $$$$\left(\mathrm{0}+{r}\:\mathrm{sin}\:\theta\right)\mathrm{tan}\:\theta+\left({x}_{{D}} −{r}+{r}\:\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow{x}_{{D}} =−{r}\left(\mathrm{1}−\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta\right) \\ $$$$ \\ $$$${area}\:{of}\:\Delta{ABV}: \\ $$$${A}_{\mathrm{1}} =\frac{\mid{x}_{{D}} \mid}{\mathrm{2}}×\left({y}_{{B}} −{y}_{{A}} \right)=\frac{{r}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta\right)}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\theta}+\mathrm{sin}\:\theta\right) \\ $$$${area}\:{of}\:{circle}\:{segment}\:{VA}: \\ $$$${A}_{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right) \\ $$$${area}\:{of}\:{parabola}\:{segment}\:{VB}: \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}}\mid{x}_{{B}} \mid{y}_{{B}} =\frac{{r}^{\mathrm{2}} }{\mathrm{48}\:\mathrm{tan}^{\mathrm{3}} \:\theta} \\ $$$$ \\ $$$${area}\:{of}\:{shaded}\:{region}: \\ $$$${A}={A}_{\mathrm{1}} −{A}_{\mathrm{2}} −{A}_{\mathrm{3}} \\ $$
Commented by ajfour last updated on 27/Dec/17

$${how}\:{do}\:{you}\:{get}\:{the}\:{parabola} \\ $$$${segment}\:{A}_{\mathrm{3}} \:{so}\:{very}\:{easily}\:{Sir}\:? \\ $$
Commented by ajfour last updated on 28/Dec/17
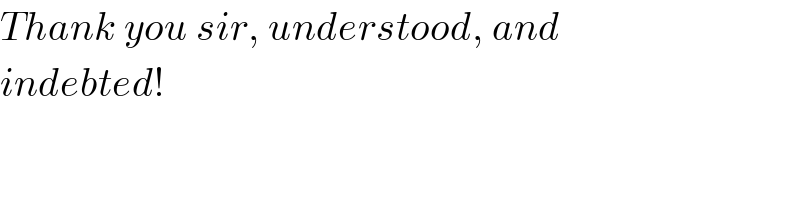
$${Thank}\:{you}\:{sir},\:{understood},\:{and} \\ $$$${indebted}! \\ $$
Commented by ajfour last updated on 27/Dec/17
thank you sir, even this much felt good to follow.., the area i understand can be done in three parts.
Commented by mrW1 last updated on 27/Dec/17
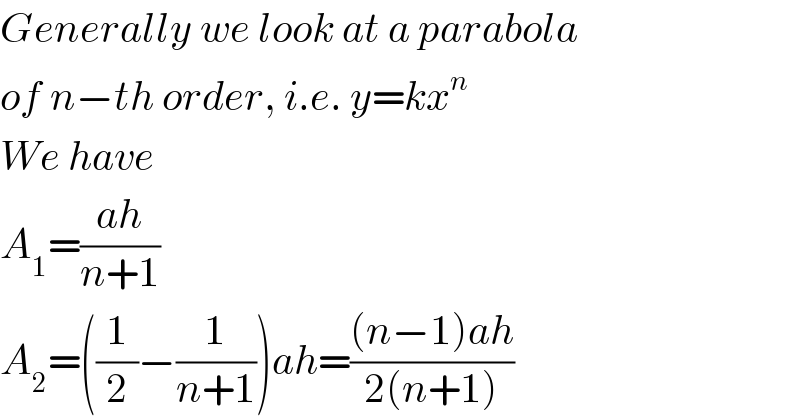
$${Generally}\:{we}\:{look}\:{at}\:{a}\:{parabola} \\ $$$${of}\:{n}−{th}\:{order},\:{i}.{e}.\:{y}={kx}^{{n}} \\ $$$${We}\:{have} \\ $$$${A}_{\mathrm{1}} =\frac{{ah}}{{n}+\mathrm{1}} \\ $$$${A}_{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right){ah}=\frac{\left({n}−\mathrm{1}\right){ah}}{\mathrm{2}\left({n}+\mathrm{1}\right)} \\ $$
Commented by ajfour last updated on 27/Dec/17
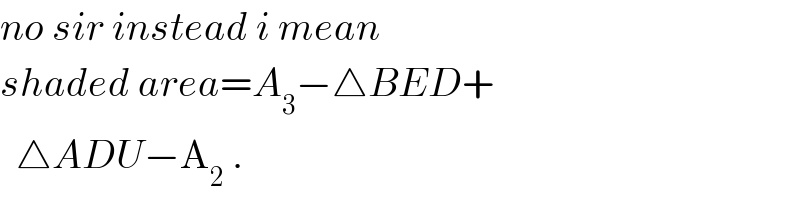
$${no}\:{sir}\:{instead}\:{i}\:{mean} \\ $$$${shaded}\:{area}={A}_{\mathrm{3}} −\bigtriangleup{BED}+ \\ $$$$\:\:\bigtriangleup{ADU}−\mathrm{A}_{\mathrm{2}} \:. \\ $$
Commented by mrW1 last updated on 27/Dec/17

Commented by mrW1 last updated on 27/Dec/17

$${You}\:{can}\:{do}\:{this}\:{sir}. \\ $$$${But}\:{following}\:{is}\:{what}\:{I}\:{used}\:{in}\:{my}\:{answer}. \\ $$
Commented by mrW1 last updated on 27/Dec/17

Commented by mrW1 last updated on 28/Dec/17
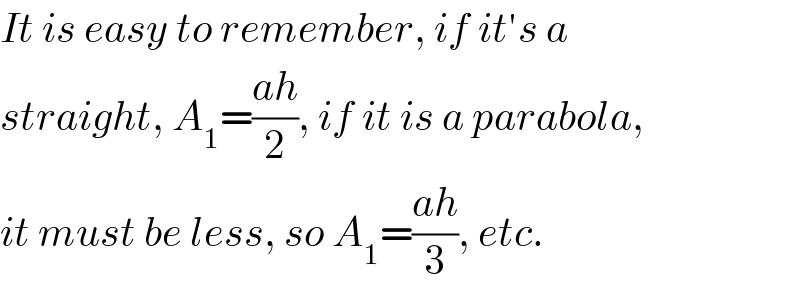
$${It}\:{is}\:{easy}\:{to}\:{remember},\:{if}\:{it}'{s}\:{a} \\ $$$${straight},\:{A}_{\mathrm{1}} =\frac{{ah}}{\mathrm{2}},\:{if}\:{it}\:{is}\:{a}\:{parabola}, \\ $$$${it}\:{must}\:{be}\:{less},\:{so}\:{A}_{\mathrm{1}} =\frac{{ah}}{\mathrm{3}},\:{etc}. \\ $$
