Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 26733 by math solver last updated on 28/Dec/17

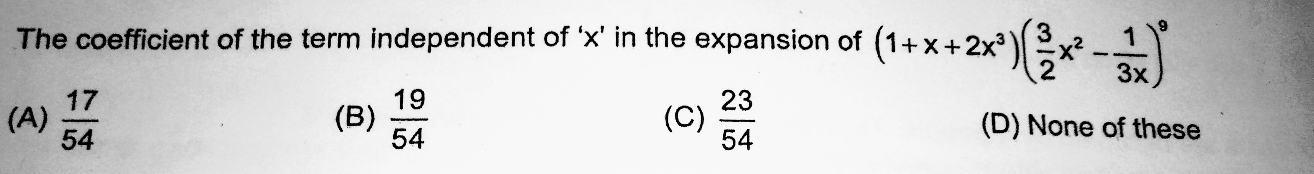
Commented by prakash jain last updated on 28/Dec/17

${(\frac{3}{2} x^{3} - \frac{1}{3 x})}^{9} =^{9} C_{i} {(\frac{3}{2})}^{i} x^{2 i} {(- 1)}^{9 - i} {(\frac{1}{3 x})}^{9 - i}$ $^{9} C_{i} {(\frac{3}{2})}^{i} {(- 1)}^{9 - i} {(\frac{1}{3})}^{9 - i} x^{4 i - 9}$ $c o e f f c i e n t o f c o n s t a n t t e r m$ $3 i - 9 = 0 \Rightarrow i = 3$ $^{9} C_{2} {(\frac{3}{2})}^{3} {(- 1)}^{9 - 3} {(\frac{1}{3})}^{9 - 3}$ $= \frac{9!}{3! 6!} \times \frac{3^{3}}{2^{3}} \times \frac{1}{3^{6}} = \frac{9 \times 8 \times 7}{1 \times 2 \times 3} \times \frac{1}{8} \times \frac{1}{3 \times 9} = \frac{7}{18}$ $3 i - 9 = - 3 \Rightarrow i = 2$ $2 \times \frac{9!}{2! 7!} \times \frac{3^{2}}{2^{2}} \times {(- 1)}^{9 - 2} \times \frac{1}{3^{7}} = \frac{9 \times 8}{4 \times 3^{5}} = - \frac{2}{27}$ $\frac{7}{18} - \frac{2}{27} = \frac{17}{54}$
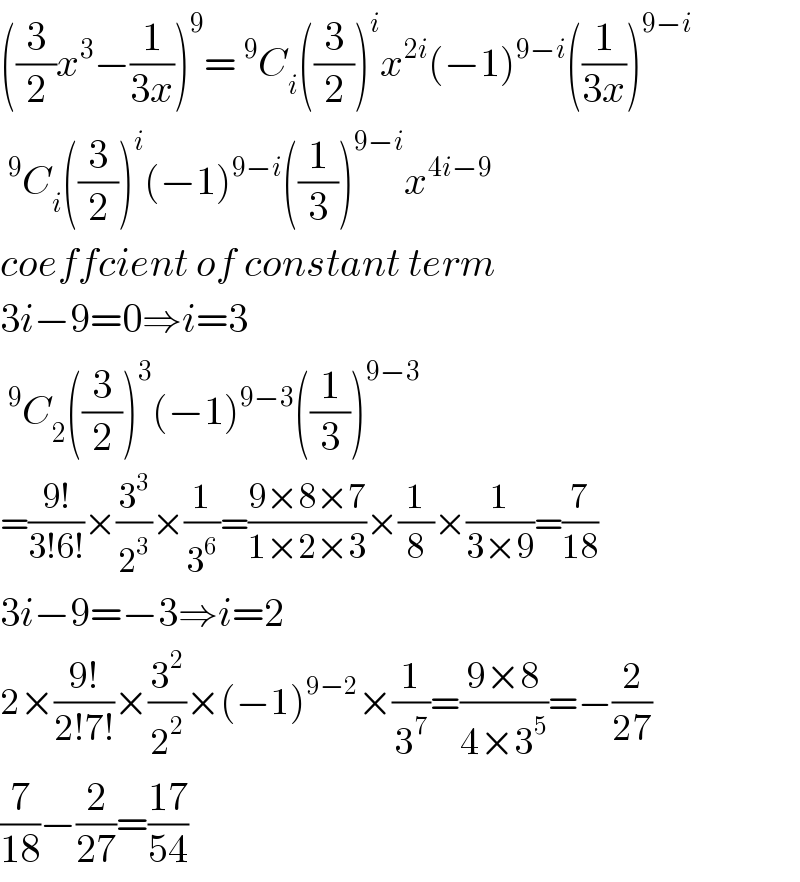
	Answered by mrW1 last updated on 28/Dec/17

	$(1 + x + 2 x^{3}) {(\frac{3}{2} x^{2} - \frac{1}{3 x})}^{9}$ $= \frac{1}{x^{9}} (1 + x + 2 x^{3}) {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9}$ $1 \times \frac{9 \times 8 \times 7}{3 \times 2 \times 1} \times {(\frac{3}{2})}^{3} {(- \frac{1}{3})}^{6} + 2 \times \frac{9 \times 8}{2 \times 1} \times {(\frac{3}{2})}^{2} {(- \frac{1}{3})}^{7}$ $= {(\frac{3}{2})}^{2} {(- \frac{1}{3})}^{6} [1 \times \frac{9 \times 8 \times 7}{3 \times 2 \times 1} \times (\frac{3}{2}) + 2 \times \frac{9 \times 8}{2 \times 1} \times (- \frac{1}{3})]$ $= {(\frac{3}{2})}^{2} {(- \frac{1}{3})}^{6} (126 - 24)$ $= \frac{1}{2^{2}} \times \frac{1}{3^{4}} \times 102$ $= \frac{17}{54}$ $\Rightarrow A n s w e r (A)$
	Commented by math solver last updated on 28/Dec/17

	$p l z e x p l a i n s t e p - 3 ?$ $h o w y o u f i n d t e r m i n d e p e n d e n t o f x ?$
	Commented by math solver last updated on 28/Dec/17

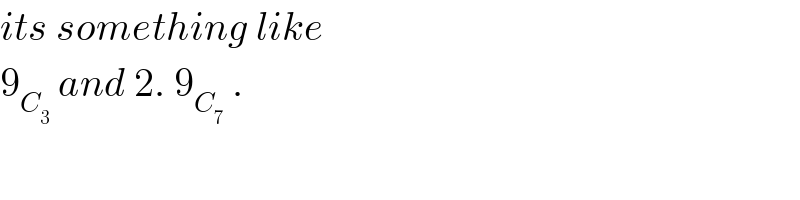
	$i t s s o m e t h i n g l i k e$ $9_{C_{3}} a n d 2 . 9_{C_{7}} .$
	Commented by mrW1 last updated on 28/Dec/17

	$x^{0} t e r m f r o m \frac{1}{x^{9}} (1 + x + 2 x^{3}) {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9}$ $\equiv x^{9} t e r m f r o m (1 + x + 2 x^{3}) {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9}$ $\equiv 1 \times x^{9} t e r m + x \times x^{8} t e r m + 2 x^{3} \times x^{6} t e r m$ $x^{9} t e r m o f {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9} i s C_{3}^{9} \times {(\frac{3}{2} x^{3})}^{3} \times {(- \frac{1}{3})}^{6}$ $t h e r e i s n o x^{8} t e r m i n {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9}$ $x^{6} t e r m o f {(\frac{3}{2} x^{3} - \frac{1}{3})}^{9} i s C_{2}^{9} \times {(\frac{3}{2} x^{3})}^{2} \times {(- \frac{1}{3})}^{7}$ $t h e r e f o r e t h e c o e f f i c i e n t o f x^{0} t e r m i s$ $1 \times C_{3}^{9} \times {(\frac{3}{2})}^{3} \times {(- \frac{1}{3})}^{6} + 2 \times C_{2}^{9} \times {(\frac{3}{2})}^{2} \times {(- \frac{1}{3})}^{7}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum