Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 2675 by prakash jain last updated on 24/Nov/15

Bases on suggestion from Filup and some discussion on that I am suggesting that we sequence, series and related function as a topic for this month. ζ(x)=Σ_(n=1) ^∞ n^(−x) , x∈R, x>1 Show that ζ(x)=(1/(Γ(x)))∫_0 ^∞ (t^(x−1) /(e^t −1))dt

$$\mathrm{Bases}\:\mathrm{on}\:\mathrm{suggestion}\:\mathrm{from}\:\mathrm{Filup}\:\mathrm{and}\:\mathrm{some} \\ $$ $$\mathrm{discussion}\:\mathrm{on}\:\mathrm{that}\:\mathrm{I}\:\mathrm{am}\:\mathrm{suggesting}\:\mathrm{that}\:\mathrm{we} \\ $$ $$\mathrm{sequence},\:\mathrm{series}\:\mathrm{and}\:\mathrm{related}\:\mathrm{function}\:\mathrm{as}\:\mathrm{a} \\ $$ $$\mathrm{topic}\:\mathrm{for}\:\mathrm{this}\:\mathrm{month}. \\ $$ $$\zeta\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{x}} ,\:{x}\in\mathbb{R},\:{x}>\mathrm{1} \\ $$ $$\mathrm{Show}\:\mathrm{that} \\ $$ $$\zeta\left({x}\right)=\frac{\mathrm{1}}{\Gamma\left({x}\right)}\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}\mathrm{d}{t} \\ $$

Commented byprakash jain last updated on 24/Nov/15

ζ−Riemann zeta function Γ−Gamma function These 2 functions were mentioned as part of some of the questions earlier. For this question only consider real numbers although the functions are defined for complex numbers as well.

$$\zeta−\mathrm{Riemann}\:\mathrm{zeta}\:\mathrm{function} \\ $$ $$\Gamma−\mathrm{Gamma}\:\mathrm{function} \\ $$ $$\mathrm{These}\:\mathrm{2}\:\mathrm{functions}\:\mathrm{were}\:\mathrm{mentioned}\:\mathrm{as}\:\mathrm{part} \\ $$ $$\mathrm{of}\:\mathrm{some}\:\mathrm{of}\:\mathrm{the}\:\mathrm{questions}\:\mathrm{earlier}. \\ $$ $$\mathrm{For}\:\mathrm{this}\:\mathrm{question}\:\mathrm{only}\:\mathrm{consider}\:\mathrm{real}\:\mathrm{numbers} \\ $$ $$\mathrm{although}\:\mathrm{the}\:\mathrm{functions}\:\mathrm{are}\:\mathrm{defined}\:\mathrm{for} \\ $$ $$\mathrm{complex}\:\mathrm{numbers}\:\mathrm{as}\:\mathrm{well}. \\ $$

Commented byRasheed Soomro last updated on 24/Nov/15

I have only heard the names of reimann zeta and gamma functions! Anyway no harm in trying! By the way who will be the judge?

$$\mathcal{I}\:{have}\:{only}\:{heard}\:{the}\:{names}\:{of}\:{reimann}\:{zeta}\:{and} \\ $$ $${gamma}\:{functions}!\:{Anyway}\:{no}\:{harm}\:{in}\:{trying}! \\ $$ $${By}\:{the}\:{way}\:{who}\:{will}\:{be}\:{the}\:{judge}? \\ $$

Commented byprakash jain last updated on 24/Nov/15

This question was not meant to be a challenge just learning details of a few things that got mentioned earlier.

$$\mathrm{This}\:\mathrm{question}\:\mathrm{was}\:\mathrm{not}\:\mathrm{meant}\:\mathrm{to}\:\mathrm{be}\:\mathrm{a} \\ $$ $$\mathrm{challenge}\:\mathrm{just}\:\mathrm{learning}\:\mathrm{details}\:\mathrm{of}\:\mathrm{a}\:\mathrm{few} \\ $$ $$\mathrm{things}\:\mathrm{that}\:\mathrm{got}\:\mathrm{mentioned}\:\mathrm{earlier}. \\ $$

Commented byprakash jain last updated on 24/Nov/15

123456 is most knowledgeable among us. (s)he will post the challenge at some point and judge us. In any case regular Q and A continues as usual from everyone.

$$\mathrm{123456}\:\mathrm{is}\:\mathrm{most}\:\mathrm{knowledgeable}\:\mathrm{among}\:\mathrm{us}. \\ $$ $$\left(\mathrm{s}\right)\mathrm{he}\:\mathrm{will}\:\mathrm{post}\:\mathrm{the}\:\mathrm{challenge}\:\mathrm{at}\:\mathrm{some}\:\mathrm{point} \\ $$ $$\mathrm{and}\:\mathrm{judge}\:\mathrm{us}. \\ $$ $$ \\ $$ $$\mathrm{In}\:\mathrm{any}\:\mathrm{case}\:\mathrm{regular}\:\mathrm{Q}\:\mathrm{and}\:\mathrm{A}\:\mathrm{continues}\:\mathrm{as} \\ $$ $$\mathrm{usual}\:\mathrm{from}\:\mathrm{everyone}. \\ $$

Commented byYozzi last updated on 24/Nov/15

Cool.

$${Cool}. \\ $$

Commented byYozzi last updated on 24/Nov/15

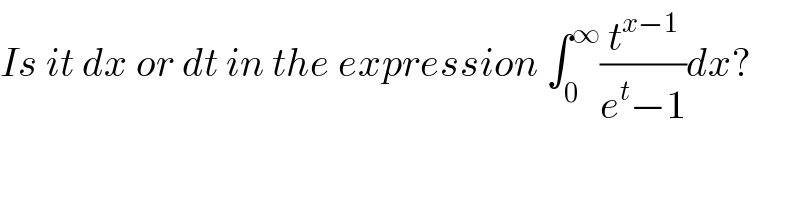
Is it dx or dt in the expression ∫_0 ^∞ (t^(x−1) /(e^t −1))dx?

$${Is}\:{it}\:{dx}\:{or}\:{dt}\:{in}\:{the}\:{expression}\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}{dx}? \\ $$

Commented byprakash jain last updated on 24/Nov/15

dt corrected.

$$\mathrm{d}{t}\:\mathrm{corrected}. \\ $$

Commented by123456 last updated on 01/Dec/15

24/12

$$\mathrm{24}/\mathrm{12} \\ $$

Answered by Yozzi last updated on 24/Nov/15

(t^(x−1) /(e^t −1))=((t^(x−1) e^(−t) )/(1−e^(−t) )) For t>0, ∣e^(−t) ∣<1. (1/(1−e^(−t) )) is the the sum of an infinite G.P with first term 1 and common ratio e^(−t) . ∴ (1/(1−e^(−t) ))=1+e^(−t) +e^(−2t) +e^(−3t) +... ∴((t^(x−1) e^(−t) )/(1−e^(−t) ))=t^(x−1) e^(−t) +t^(x−1) e^(−2t) +t^(x−1) e^(−3t) +... ((t^(x−1) e^(−t) )/(1−e^(−t) ))=Σ_(r=1) ^∞ t^(x−1) e^(−rt) Let I=∫_0 ^∞ (t^(x−1) /(e^t −1))dt=∫_0 ^∞ (Σ_(r=1) ^∞ t^(x−1) e^(−rt) )dt I=Σ_(r=1) ^∞ (∫_0 ^∞ t^(x−1) e^(−rt) dt) let u=rt⇒t=(1/r)u⇒(1/r)du=dt At t=0,u=0. As t→∞, u→∞ for r>0. ∴t^(x−1) =r^(1−x) u^(x−1) ∴∫_0 ^∞ t^(x−1) e^(−rt) dt=∫_0 ^∞ r^(1−x) u^(x−1) e^(−u) ×(1/r)du =r^(−x) ∫_0 ^∞ u^(x−1) e^(−u) du The gamma function Γ(x) defined for x>0 is expressible as Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt. ∴∫_0 ^∞ t^(x−1) e^(−rt) dt=r^(−x) Γ(x) ∴I=Γ(x)×Σ_(r=1) ^∞ r^(−x) But, ζ(x)=Σ_(r=1) ^∞ r^(−x) ,x∈R,x>1. ∴I=Γ(x)ζ(x)⇒ζ(x)=(1/(Γ(x)))∫_0 ^∞ (t^(x−1) /(e^t −1))dt

$$\frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}=\frac{{t}^{{x}−\mathrm{1}} {e}^{−{t}} }{\mathrm{1}−{e}^{−{t}} } \\ $$ $${For}\:{t}>\mathrm{0},\:\:\mid{e}^{−{t}} \mid<\mathrm{1}.\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{t}} }\:{is}\:{the}\:{the} \\ $$ $${sum}\:{of}\:{an}\:{infinite}\:{G}.{P}\:{with}\:{first}\:{term} \\ $$ $$\mathrm{1}\:{and}\:{common}\:{ratio}\:{e}^{−{t}} . \\ $$ $$\therefore\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{t}} }=\mathrm{1}+{e}^{−{t}} +{e}^{−\mathrm{2}{t}} +{e}^{−\mathrm{3}{t}} +... \\ $$ $$\therefore\frac{{t}^{{x}−\mathrm{1}} {e}^{−{t}} }{\mathrm{1}−{e}^{−{t}} }={t}^{{x}−\mathrm{1}} {e}^{−{t}} +{t}^{{x}−\mathrm{1}} {e}^{−\mathrm{2}{t}} +{t}^{{x}−\mathrm{1}} {e}^{−\mathrm{3}{t}} +... \\ $$ $$\frac{{t}^{{x}−\mathrm{1}} {e}^{−{t}} }{\mathrm{1}−{e}^{−{t}} }=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{t}^{{x}−\mathrm{1}} {e}^{−{rt}} \\ $$ $${Let}\:{I}=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}{dt}=\int_{\mathrm{0}} ^{\infty} \left(\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{t}^{{x}−\mathrm{1}} {e}^{−{rt}} \right){dt} \\ $$ $${I}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{rt}} {dt}\right) \\ $$ $${let}\:{u}={rt}\Rightarrow{t}=\frac{\mathrm{1}}{{r}}{u}\Rightarrow\frac{\mathrm{1}}{{r}}{du}={dt} \\ $$ $${At}\:{t}=\mathrm{0},{u}=\mathrm{0}.\:{As}\:{t}\rightarrow\infty,\:{u}\rightarrow\infty\:{for}\:{r}>\mathrm{0}. \\ $$ $$\therefore{t}^{{x}−\mathrm{1}} ={r}^{\mathrm{1}−{x}} {u}^{{x}−\mathrm{1}} \\ $$ $$\therefore\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{rt}} {dt}=\int_{\mathrm{0}} ^{\infty} {r}^{\mathrm{1}−{x}} {u}^{{x}−\mathrm{1}} {e}^{−{u}} ×\frac{\mathrm{1}}{{r}}{du} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={r}^{−{x}} \int_{\mathrm{0}} ^{\infty} {u}^{{x}−\mathrm{1}} {e}^{−{u}} {du} \\ $$ $${The}\:{gamma}\:{function}\:\Gamma\left({x}\right)\:{defined} \\ $$ $${for}\:{x}>\mathrm{0}\:{is}\:{expressible}\:{as} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}. \\ $$ $$\therefore\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{rt}} {dt}={r}^{−{x}} \Gamma\left({x}\right) \\ $$ $$\therefore{I}=\Gamma\left({x}\right)×\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{r}^{−{x}} \\ $$ $${But},\:\zeta\left({x}\right)=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}{r}^{−{x}} \:\:,{x}\in\mathbb{R},{x}>\mathrm{1}. \\ $$ $$\therefore{I}=\Gamma\left({x}\right)\zeta\left({x}\right)\Rightarrow\zeta\left({x}\right)=\frac{\mathrm{1}}{\Gamma\left({x}\right)}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} −\mathrm{1}}{dt}\: \\ $$ $$ \\ $$

Commented by123456 last updated on 24/Nov/15

nice

$$\mathrm{nice} \\ $$

Commented byFilup last updated on 25/Nov/15

Awesome! I had no idea how to do this one! So simple!

$${Awesome}!\:\mathrm{I}\:\mathrm{had}\:\mathrm{no}\:\mathrm{idea}\:\mathrm{how}\:\mathrm{to}\:\mathrm{do}\:\mathrm{this} \\ $$ $$\mathrm{one}!\:{S}\mathrm{o}\:\mathrm{simple}! \\ $$

Commented byRasheed Soomro last updated on 25/Nov/15

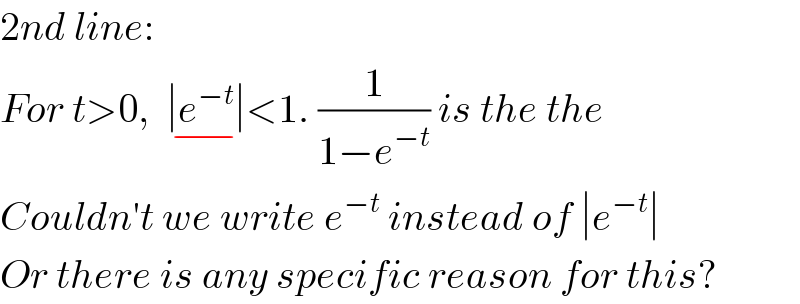
2nd line: For t>0, ∣e^(−t) ∣_(−) <1. (1/(1−e^(−t) )) is the the Couldn′t we write e^(−t) instead of ∣e^(−t) ∣ Or there is any specific reason for this?

$$\mathrm{2}{nd}\:{line}: \\ $$ $${For}\:{t}>\mathrm{0},\:\:\underset{−} {\mid{e}^{−{t}} \mid}<\mathrm{1}.\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{t}} }\:{is}\:{the}\:{the} \\ $$ $${Couldn}'{t}\:{we}\:{write}\:{e}^{−{t}} \:{instead}\:{of}\:\mid{e}^{−{t}} \mid \\ $$ $${Or}\:{there}\:{is}\:{any}\:{specific}\:{reason}\:{for}\:{this}? \\ $$

Commented byYozzi last updated on 25/Nov/15

It′s written like that to specifically indicate that the convergence condition for an infinite geometric series is satisfied. So expressions of the form (c/(1−dx)) represent the sum of an infinite geometric series under the condition that ∣dx∣<1⇒∣x∣<1/d (d≠0). The series is then deduced to be of the form cΣ_(n=1) ^∞ (dx)^(n−1) =c{1+dx+d^2 x^2 +d^3 x^3 +...} =c+cdx+cd^2 x^2 +cd^3 x^3 +... If dx=0 because d=0 or x=0 we get (c/(1−dx))=(c/(1−0))=c which is equal to cΣ_(n=1) ^∞ 0^(n−1) =c{1+0+0+0+...}=c.

$${It}'{s}\:{written}\:{like}\:{that}\:{to}\:{specifically} \\ $$ $${indicate}\:{that}\:{the}\:{convergence} \\ $$ $${condition}\:{for}\:{an}\:{infinite}\:{geometric} \\ $$ $${series}\:{is}\:{satisfied}.\:{So}\:{expressions} \\ $$ $${of}\:{the}\:{form}\: \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{c}}{\mathrm{1}−{dx}}\:\: \\ $$ $${represent}\:{the}\:{sum}\:{of}\:{an}\:{infinite}\: \\ $$ $${geometric}\:{series}\:{under}\:{the}\:{condition} \\ $$ $${that}\:\mid{dx}\mid<\mathrm{1}\Rightarrow\mid{x}\mid<\mathrm{1}/{d}\:\:\left({d}\neq\mathrm{0}\right).\:{The} \\ $$ $${series}\:{is}\:{then}\:{deduced}\:{to}\:{be}\:{of}\:{the}\:{form} \\ $$ $${c}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({dx}\right)^{{n}−\mathrm{1}} ={c}\left\{\mathrm{1}+{dx}+{d}^{\mathrm{2}} {x}^{\mathrm{2}} +{d}^{\mathrm{3}} {x}^{\mathrm{3}} +...\right\} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={c}+{cdx}+{cd}^{\mathrm{2}} {x}^{\mathrm{2}} +{cd}^{\mathrm{3}} {x}^{\mathrm{3}} +... \\ $$ $${If}\:{dx}=\mathrm{0}\:{because}\:{d}=\mathrm{0}\:{or}\:{x}=\mathrm{0} \\ $$ $${we}\:{get}\:\frac{{c}}{\mathrm{1}−{dx}}=\frac{{c}}{\mathrm{1}−\mathrm{0}}={c}\:{which}\:{is}\:{equal} \\ $$ $${to}\:{c}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{0}^{{n}−\mathrm{1}} ={c}\left\{\mathrm{1}+\mathrm{0}+\mathrm{0}+\mathrm{0}+...\right\}={c}. \\ $$ $$\:\:\:\:\:\:\:\:\:\: \\ $$ $$ \\ $$ $$ \\ $$

Commented byRasheed Soomro last updated on 25/Nov/15

Th^a nkS

$$\mathcal{T}{h}^{{a}} {nk}\mathcal{S} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com