Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 26756 by abdo imad last updated on 28/Dec/17

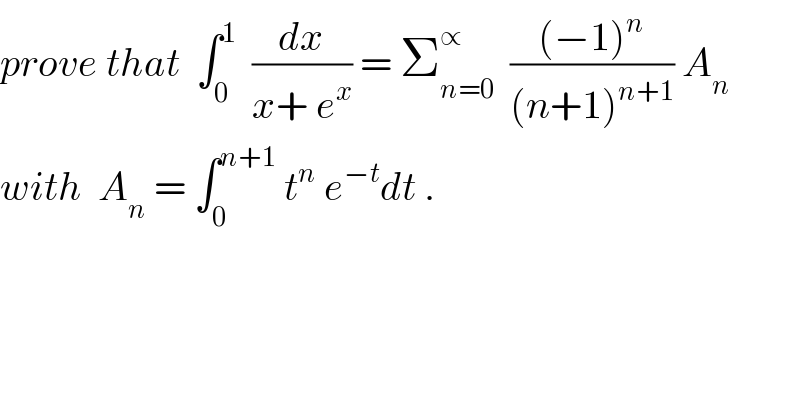
prove that ∫_0 ^1 (dx/(x+ e^x )) = Σ_(n=0) ^∝ (((−1)^n )/((n+1)^(n+1) )) A_n with A_n = ∫_0 ^(n+1) t^n e^(−t) dt .

$${prove}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}+\:{e}^{{x}} }\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:{A}_{{n}} \\ $$$${with}\:\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{{n}+\mathrm{1}} \:{t}^{{n}} \:{e}^{−{t}} {dt}\:. \\ $$

Commented by abdo imad last updated on 01/Jan/18

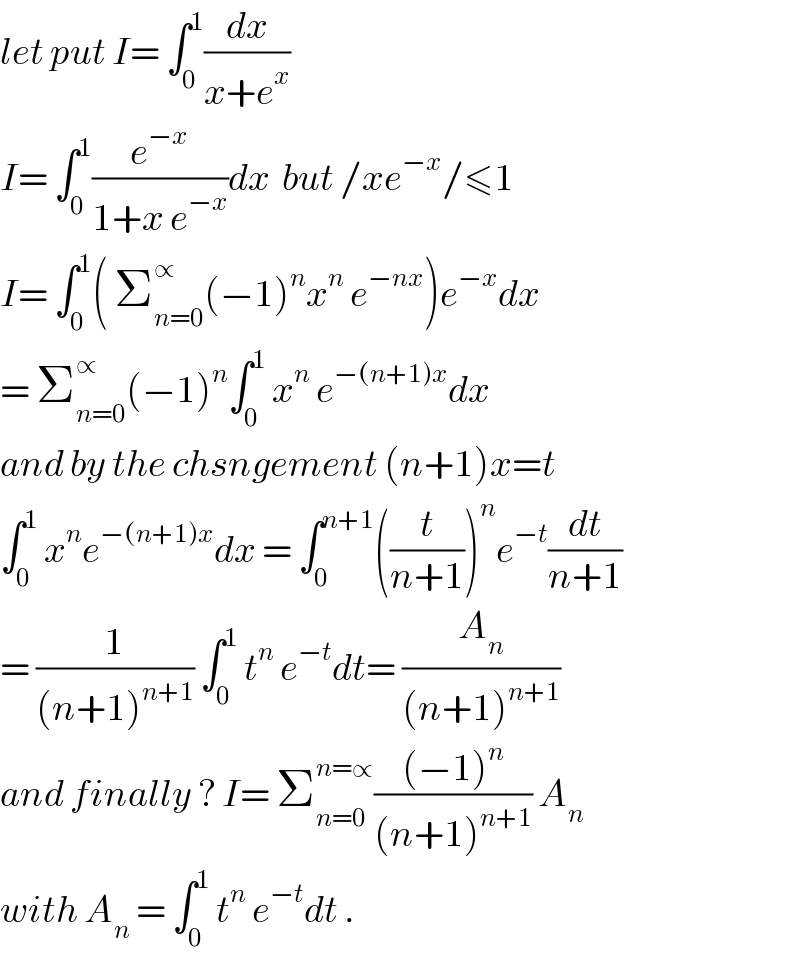
let put I= ∫_0 ^1 (dx/(x+e^x )) I= ∫_0 ^1 (e^(−x) /(1+x e^(−x) ))dx but /xe^(−x) /≤1 I= ∫_0 ^1 ( Σ_(n=0) ^∝ (−1)^n x^n e^(−nx) )e^(−x) dx = Σ_(n=0) ^∝ (−1)^n ∫_0 ^1 x^n e^(−(n+1)x) dx and by the chsngement (n+1)x=t ∫_0 ^1 x^n e^(−(n+1)x) dx = ∫_0 ^(n+1) ((t/(n+1)))^n e^(−t) (dt/(n+1)) = (1/((n+1)^(n+1) )) ∫_0 ^1 t^n e^(−t) dt= (A_n /((n+1)^(n+1) )) and finally ? I= Σ_(n=0) ^(n=∝) (((−1)^n )/((n+1)^(n+1) )) A_n with A_n = ∫_0 ^1 t^n e^(−t) dt .

$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}+{e}^{{x}} } \\ $$$${I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{−{x}} }{\mathrm{1}+{x}\:{e}^{−{x}} }{dx}\:\:{but}\:/{xe}^{−{x}} /\leqslant\mathrm{1} \\ $$$${I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:{e}^{−{nx}} \right){e}^{−{x}} {dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{e}^{−\left({n}+\mathrm{1}\right){x}} {dx} \\ $$$${and}\:{by}\:{the}\:{chsngement}\:\left({n}+\mathrm{1}\right){x}={t} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} {e}^{−\left({n}+\mathrm{1}\right){x}} {dx}\:=\:\int_{\mathrm{0}} ^{{n}+\mathrm{1}} \left(\frac{{t}}{{n}+\mathrm{1}}\right)^{{n}} {e}^{−{t}} \frac{{dt}}{{n}+\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \:{e}^{−{t}} {dt}=\:\frac{{A}_{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} } \\ $$$${and}\:{finally}\:?\:{I}=\:\sum_{{n}=\mathrm{0}} ^{{n}=\propto} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:{A}_{{n}} \\ $$$${with}\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} \:{e}^{−{t}} {dt}\:. \\ $$

Commented by abdo imad last updated on 01/Jan/18

∫_0 ^1 x^n e^(−(n+1)x) dx=(1/((n+1)^(n+1) )) ∫_0 ^(n+1) t^n e^(−t) dt = (A_n /((n+1)^(n+1) )) with A_n = ∫_0 ^(n+1) t^n e^(−t) dt.

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {e}^{−\left({n}+\mathrm{1}\right){x}} {dx}=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{{n}+\mathrm{1}} {t}^{{n}} \:{e}^{−{t}} {dt} \\ $$$$=\:\frac{{A}_{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:{with}\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{{n}+\mathrm{1}} {t}^{{n}} {e}^{−{t}} {dt}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com