
Question Number 26941 by Mr eaay last updated on 31/Dec/17

$${show}\:{that}\:{the}\:{rectangular}\:{solid}\:\:{of}\: \\ $$$${naximum}\:{volume}\:{that}\:{can}\:{be}\:{inscribed} \\ $$$${into}\:{a}\:{sphere}\:{is}\:{a}\:{cube} \\ $$
Answered by mrW1 last updated on 01/Jan/18
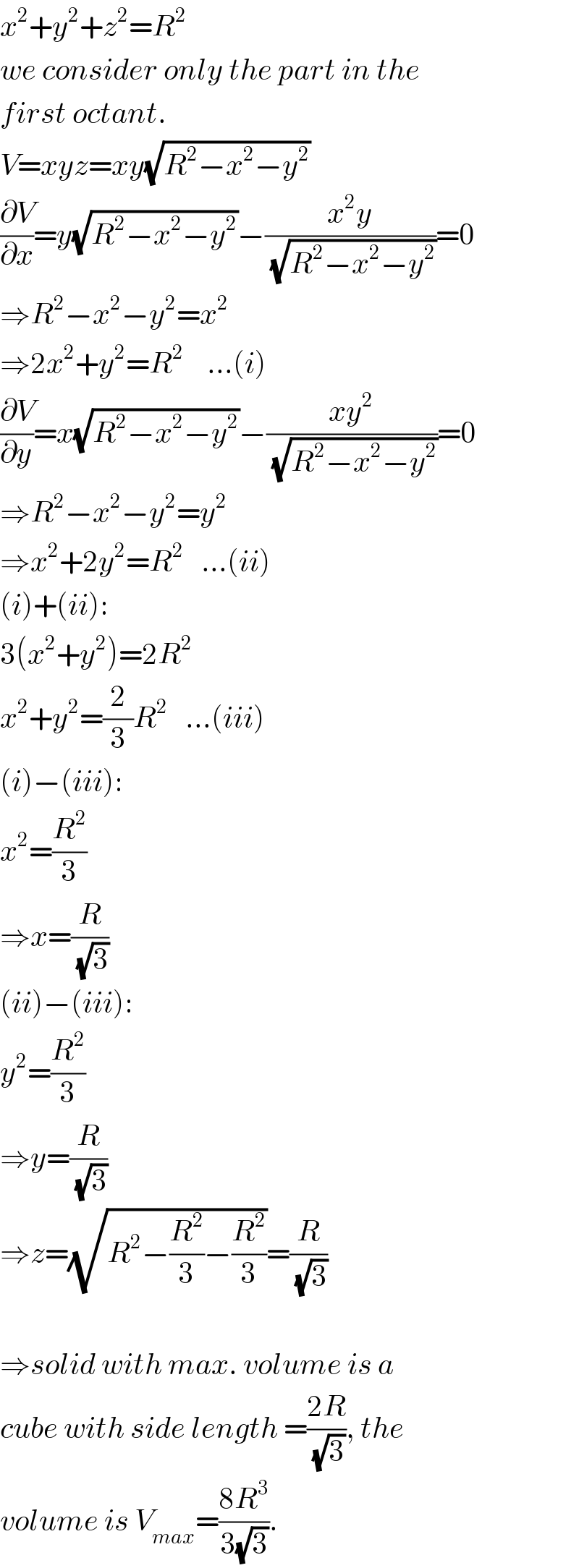
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${we}\:{consider}\:{only}\:{the}\:{part}\:{in}\:{the} \\ $$$${first}\:{octant}. \\ $$$${V}={xyz}={xy}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\frac{\partial{V}}{\partial{x}}={y}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }−\frac{{x}^{\mathrm{2}} {y}}{\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:\:...\left({i}\right) \\ $$$$\frac{\partial{V}}{\partial{y}}={x}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }−\frac{{xy}^{\mathrm{2}} }{\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow{R}^{\mathrm{2}} −{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={y}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{2}{R}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}{R}^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)−\left({iii}\right): \\ $$$${x}^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow{x}=\frac{{R}}{\sqrt{\mathrm{3}}} \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$${y}^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow{y}=\frac{{R}}{\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{z}=\sqrt{{R}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{3}}−\frac{{R}^{\mathrm{2}} }{\mathrm{3}}}=\frac{{R}}{\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\Rightarrow{solid}\:{with}\:{max}.\:{volume}\:{is}\:{a} \\ $$$${cube}\:{with}\:{side}\:{length}\:=\frac{\mathrm{2}{R}}{\sqrt{\mathrm{3}}},\:{the} \\ $$$${volume}\:{is}\:{V}_{{max}} =\frac{\mathrm{8}{R}^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{3}}}. \\ $$
