Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 26997 by abdo imad last updated on 01/Jan/18

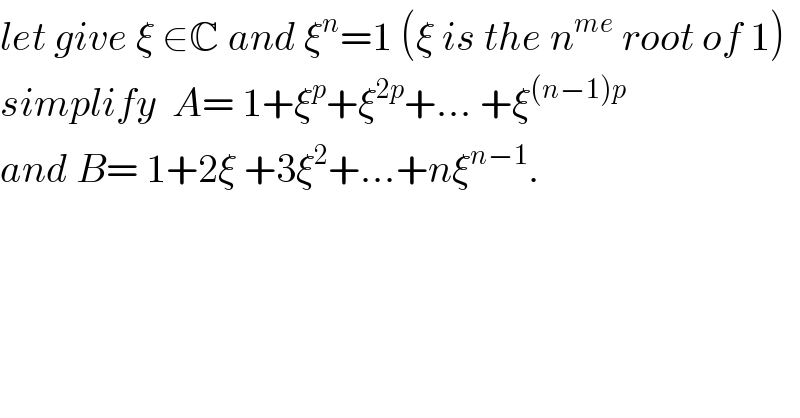
let give ξ ∈C and ξ^n =1 (ξ is the n^(me) root of 1) simplify A= 1+ξ^p +ξ^(2p) +... +ξ^((n−1)p) and B= 1+2ξ +3ξ^2 +...+nξ^(n−1) .

$${let}\:{give}\:\xi\:\in\mathbb{C}\:{and}\:\xi^{{n}} =\mathrm{1}\:\left(\xi\:{is}\:{the}\:{n}^{{me}} \:{root}\:{of}\:\mathrm{1}\right) \\ $$$${simplify}\:\:{A}=\:\mathrm{1}+\xi^{{p}} +\xi^{\mathrm{2}{p}} +...\:+\xi^{\left({n}−\mathrm{1}\right){p}} \\ $$$${and}\:{B}=\:\mathrm{1}+\mathrm{2}\xi\:+\mathrm{3}\xi^{\mathrm{2}} +...+{n}\xi^{{n}−\mathrm{1}} . \\ $$

Commented by prakash jain last updated on 01/Jan/18

A=((ξ^(np) −1)/(ξ^p −1))=(((ξ^n )^p −1)/(ξ^p −1))=0 if ξ^p ≠1 A=n if ξ^p =1

$${A}=\frac{\xi^{{np}} −\mathrm{1}}{\xi^{{p}} −\mathrm{1}}=\frac{\left(\xi^{{n}} \right)^{{p}} −\mathrm{1}}{\xi^{{p}} −\mathrm{1}}=\mathrm{0}\:\mathrm{if}\:\xi^{{p}} \neq\mathrm{1} \\ $$$${A}={n}\:\mathrm{if}\:\xi^{{p}} =\mathrm{1} \\ $$

Commented by abdo imad last updated on 02/Jan/18

value of A if ξ^p =1 A= n if ξ^p ≠1 A= Σ_(k=0) ^(n−1) ξ^(kp) = ((1− (ξ^p )^n )/(1−ξ^p )) =((1−(ξ^n )^p )/(1−ξ^p )) =0 value of B if ξ=1 B=1+2+3+....+n =((n(n+1))/2) if ξ≠1 B= p(x) with p(x)= 1+2x +3x^2 +....+nx^(n−1) and x≠1 we have ∫p(x)dx= x +x^2 +x^3 +....+x^n +λ λ=p(0)=1⇒p(x)= 1+x+x^2 +...+x^n =((x^(n+1) −1)/(x−1)) ⇒p(x)=(d/dx)(((x^(n+1) −1)/(x−1))) =(((n+1)x^n (x−1)−(x^(n+1) −1))/((x−1)^2 )) =(((n+1)x^(n+1) −(n+1)x^n −x^(n+1) +1)/((x−1)^2 )) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^(2 ) )) and with ξ^n =1 B=p(ξ)= ((nξ^(n+1) −(n+1)ξ +1)/((ξ−1)^2 )) B= ((nξ −nξ +1−ξ)/((1−ξ)^2 )) ⇒B= (1/(1−ξ)) .

$${value}\:{of}\:{A} \\ $$$${if}\:\xi^{{p}} =\mathrm{1}\:\:{A}=\:{n} \\ $$$${if}\:\xi^{{p}} \neq\mathrm{1}\:\:{A}=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\xi^{{kp}} \:=\:\frac{\mathrm{1}−\:\left(\xi^{{p}} \right)^{{n}} }{\mathrm{1}−\xi^{{p}} } \\ $$$$=\frac{\mathrm{1}−\left(\xi^{{n}} \right)^{{p}} }{\mathrm{1}−\xi^{{p}} }\:=\mathrm{0} \\ $$$${value}\:{of}\:{B} \\ $$$${if}\:\xi=\mathrm{1}\:\:\:{B}=\mathrm{1}+\mathrm{2}+\mathrm{3}+....+{n}\:=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${if}\:\xi\neq\mathrm{1}\:\:{B}=\:{p}\left({x}\right)\:{with}\:\:{p}\left({x}\right)=\:\mathrm{1}+\mathrm{2}{x}\:+\mathrm{3}{x}^{\mathrm{2}} +....+{nx}^{{n}−\mathrm{1}} \\ $$$${and}\:{x}\neq\mathrm{1}\:{we}\:{have} \\ $$$$\int{p}\left({x}\right){dx}=\:{x}\:+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \:+....+{x}^{{n}} \:+\lambda \\ $$$$\lambda={p}\left(\mathrm{0}\right)=\mathrm{1}\Rightarrow{p}\left({x}\right)=\:\mathrm{1}+{x}+{x}^{\mathrm{2}} +...+{x}^{{n}} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\:\:\Rightarrow{p}\left({x}\right)=\frac{{d}}{{dx}}\left(\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$=\frac{\left({n}+\mathrm{1}\right){x}^{{n}} \left({x}−\mathrm{1}\right)−\left({x}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} \:−{x}^{{n}+\mathrm{1}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{{nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}\:} }\:{and}\:{with}\:\xi^{{n}} =\mathrm{1} \\ $$$${B}={p}\left(\xi\right)=\:\frac{{n}\xi^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\xi\:+\mathrm{1}}{\left(\xi−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${B}=\:\frac{{n}\xi\:−{n}\xi\:+\mathrm{1}−\xi}{\left(\mathrm{1}−\xi\right)^{\mathrm{2}} }\:\Rightarrow{B}=\:\frac{\mathrm{1}}{\mathrm{1}−\xi}\:. \\ $$$$ \\ $$

Commented by abdo imad last updated on 01/Jan/18

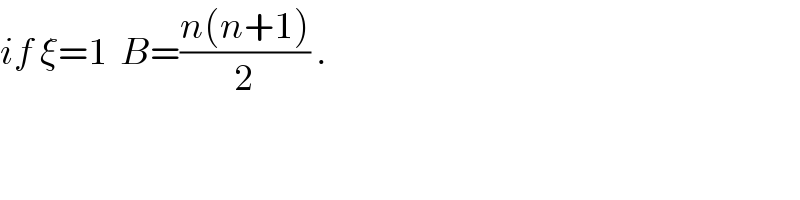
if ξ=1 B=((n(n+1))/2) .

$${if}\:\xi=\mathrm{1}\:\:{B}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com