Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 27 by user1 last updated on 25/Jan/15

If f=x^2 zi−2y^3 z^2 j+xy^2 zk. Find div f, curl f, at(1, −1, 1).

$$\mathrm{If}\:\boldsymbol{\mathrm{f}}={x}^{\mathrm{2}} {z}\boldsymbol{\mathrm{i}}−\mathrm{2}{y}^{\mathrm{3}} {z}^{\mathrm{2}} \boldsymbol{\mathrm{j}}+{xy}^{\mathrm{2}} {z}\boldsymbol{\mathrm{k}}.\:\mathrm{Find}\:{div}\:\boldsymbol{\mathrm{f}},\:{curl}\:\boldsymbol{\mathrm{f}},\: \\ $$$${at}\left(\mathrm{1},\:−\mathrm{1},\:\mathrm{1}\right). \\ $$

Answered by user1 last updated on 03/Nov/14

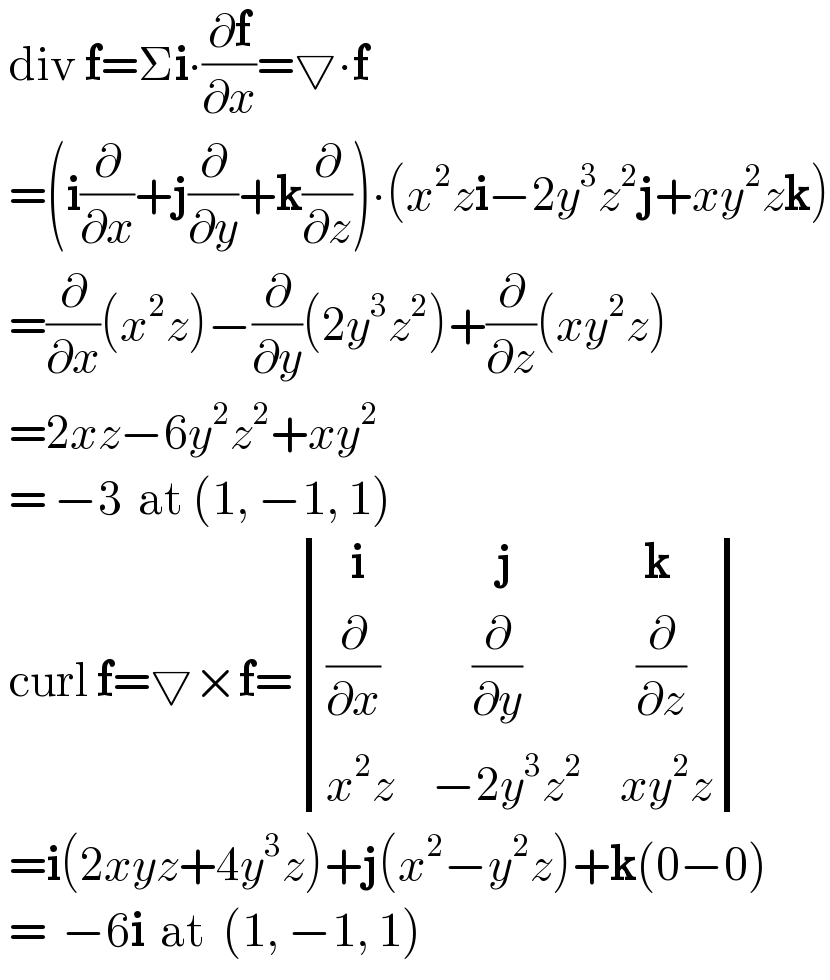
div f=Σi∙(∂f/∂x)=▽∙f =(i(∂/∂x)+j(∂/∂y)+k(∂/∂z))∙(x^2 zi−2y^3 z^2 j+xy^2 zk) =(∂/∂x)(x^2 z)−(∂/∂y)(2y^3 z^2 )+(∂/∂z)(xy^2 z) =2xz−6y^2 z^2 +xy^2 = −3 at (1, −1, 1) curl f=▽×f= determinant ((( i),( j),( k)),((∂/∂x),( (∂/∂y)),( (∂/∂z))),((x^2 z),(−2y^3 z^2 ),(xy^2 z))) =i(2xyz+4y^3 z)+j(x^2 −y^2 z)+k(0−0) = −6i at (1, −1, 1)

$$\:\mathrm{div}\:\boldsymbol{\mathrm{f}}=\Sigma\boldsymbol{\mathrm{i}}\centerdot\frac{\partial\boldsymbol{\mathrm{f}}}{\partial{x}}=\bigtriangledown\centerdot\boldsymbol{\mathrm{f}} \\ $$$$\:=\left(\boldsymbol{\mathrm{i}}\frac{\partial}{\partial{x}}+\boldsymbol{\mathrm{j}}\frac{\partial}{\partial{y}}+\boldsymbol{\mathrm{k}}\frac{\partial}{\partial{z}}\right)\centerdot\left({x}^{\mathrm{2}} {z}\boldsymbol{\mathrm{i}}−\mathrm{2}{y}^{\mathrm{3}} {z}^{\mathrm{2}} \boldsymbol{\mathrm{j}}+{xy}^{\mathrm{2}} {z}\boldsymbol{\mathrm{k}}\right) \\ $$$$\:=\frac{\partial}{\partial{x}}\left({x}^{\mathrm{2}} {z}\right)−\frac{\partial}{\partial{y}}\left(\mathrm{2}{y}^{\mathrm{3}} {z}^{\mathrm{2}} \right)+\frac{\partial}{\partial{z}}\left({xy}^{\mathrm{2}} {z}\right) \\ $$$$\:=\mathrm{2}{xz}−\mathrm{6}{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{xy}^{\mathrm{2}} \\ $$$$\:=\:−\mathrm{3}\:\:\mathrm{at}\:\left(\mathrm{1},\:−\mathrm{1},\:\mathrm{1}\right)\: \\ $$$$\:\mathrm{curl}\:\boldsymbol{\mathrm{f}}=\bigtriangledown×\boldsymbol{\mathrm{f}}=\begin{vmatrix}{\:\:\:\boldsymbol{\mathrm{i}}}&{\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{j}}}&{\:\:\:\boldsymbol{\mathrm{k}}}\\{\frac{\partial}{\partial{x}}}&{\:\:\:\:\:\frac{\partial}{\partial{y}}}&{\:\:\frac{\partial}{\partial{z}}}\\{{x}^{\mathrm{2}} {z}}&{−\mathrm{2}{y}^{\mathrm{3}} {z}^{\mathrm{2}} }&{{xy}^{\mathrm{2}} {z}}\end{vmatrix} \\ $$$$\:=\boldsymbol{\mathrm{i}}\left(\mathrm{2}{xyz}+\mathrm{4}{y}^{\mathrm{3}} {z}\right)+\boldsymbol{\mathrm{j}}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} {z}\right)+\boldsymbol{\mathrm{k}}\left(\mathrm{0}−\mathrm{0}\right) \\ $$$$\:=\:\:−\mathrm{6}\boldsymbol{\mathrm{i}}\:\:\mathrm{at}\:\:\left(\mathrm{1},\:−\mathrm{1},\:\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com