Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 2702 by Filup last updated on 25/Nov/15

ζ(s)=Σ_(i=1) ^∞ i^(−s) =1+(1/2^s )+(1/3^s )+... Is ζ(s)>0∀s∈R? 1. Can you prove, or prove otherwise? 2. If ζ(s)>n, s∈R, what are the bounds of s? i.e. a≤s≤b : ζ(s)>n

$$\zeta\left({s}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{−{s}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+... \\ $$ $$ \\ $$ $$\mathrm{Is}\:\zeta\left({s}\right)>\mathrm{0}\forall{s}\in\mathbb{R}? \\ $$ $$\mathrm{1}.\:\mathrm{Can}\:\mathrm{you}\:\mathrm{prove},\:\mathrm{or}\:\mathrm{prove}\:\mathrm{otherwise}? \\ $$ $$\mathrm{2}.\:\mathrm{If}\:\zeta\left({s}\right)>{n},\:{s}\in\mathbb{R},\:\mathrm{what}\:\mathrm{are}\:\mathrm{the}\:\mathrm{bounds} \\ $$ $$\mathrm{of}\:{s}?\:\mathrm{i}.\mathrm{e}.\:\:{a}\leqslant{s}\leqslant{b}\::\:\zeta\left({s}\right)>{n} \\ $$

Commented byFilup last updated on 25/Nov/15

i have actually solved that about a week ago. ill post it later I have work now i′ll make a new post later with the proof

$$\mathrm{i}\:\mathrm{have}\:\mathrm{actually}\:\mathrm{solved}\:\mathrm{that}\:\mathrm{ab}{o}\mathrm{ut}\:\mathrm{a}\:\mathrm{week} \\ $$ $$\mathrm{ago}.\:\mathrm{ill}\:\mathrm{post}\:\mathrm{it}\:\mathrm{later} \\ $$ $$\mathrm{I}\:{have}\:{work}\:\mathrm{now} \\ $$ $$ \\ $$ $$\mathrm{i}'\mathrm{ll}\:\mathrm{make}\:\mathrm{a}\:\mathrm{new}\:\mathrm{post}\:\mathrm{later}\:\mathrm{with}\:\mathrm{the}\:\mathrm{proof} \\ $$

Commented byFilup last updated on 25/Nov/15

Feel free to express ζ(s) in other froms of notation (such as in terms of Γ and integral notation)

$$\mathrm{Feel}\:\mathrm{free}\:\mathrm{to}\:\mathrm{express}\:\zeta\left({s}\right)\:\mathrm{in}\:\mathrm{other}\:\mathrm{froms} \\ $$ $$\mathrm{of}\:\mathrm{notation}\:\left({such}\:{as}\:{in}\:{terms}\:{of}\right. \\ $$ $$\left.\Gamma\:{and}\:{integral}\:{notation}\right) \\ $$

Commented byprakash jain last updated on 25/Nov/15

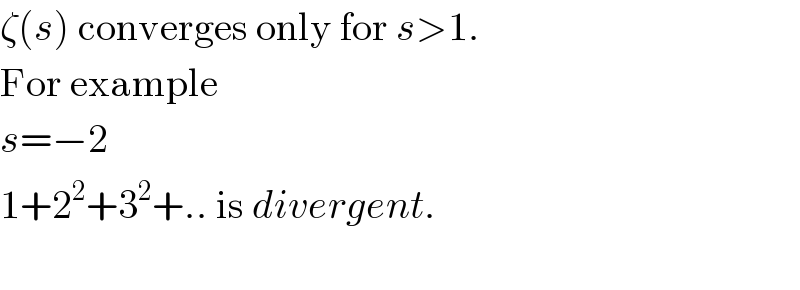
ζ(s) converges only for s>1. For example s=−2 1+2^2 +3^2 +.. is divergent.

$$\zeta\left({s}\right)\:\mathrm{converges}\:\mathrm{only}\:\mathrm{for}\:{s}>\mathrm{1}. \\ $$ $$\mathrm{For}\:\mathrm{example} \\ $$ $${s}=−\mathrm{2} \\ $$ $$\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +..\:\mathrm{is}\:{divergent}. \\ $$ $$ \\ $$

Commented by123456 last updated on 25/Nov/15

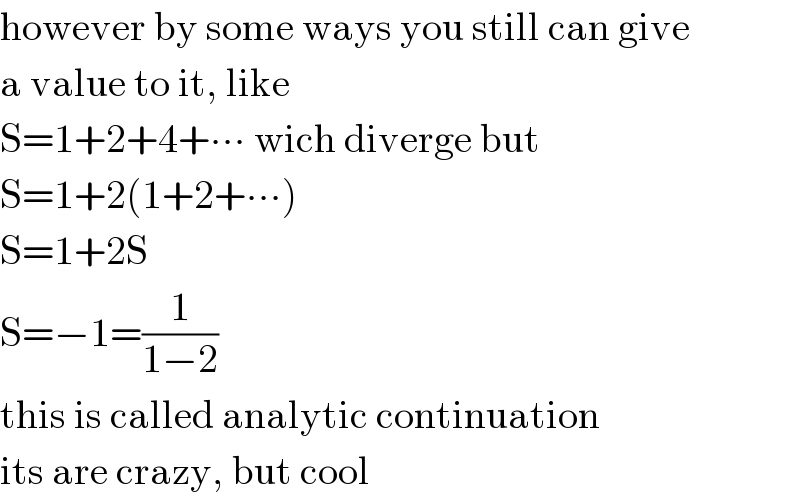
however by some ways you still can give a value to it, like S=1+2+4+∙∙∙ wich diverge but S=1+2(1+2+∙∙∙) S=1+2S S=−1=(1/(1−2)) this is called analytic continuation its are crazy, but cool

$$\mathrm{however}\:\mathrm{by}\:\mathrm{some}\:\mathrm{ways}\:\mathrm{you}\:\mathrm{still}\:\mathrm{can}\:\mathrm{give} \\ $$ $$\mathrm{a}\:\mathrm{value}\:\mathrm{to}\:\mathrm{it},\:\mathrm{like} \\ $$ $$\mathrm{S}=\mathrm{1}+\mathrm{2}+\mathrm{4}+\centerdot\centerdot\centerdot\:\mathrm{wich}\:\mathrm{diverge}\:\mathrm{but} \\ $$ $$\mathrm{S}=\mathrm{1}+\mathrm{2}\left(\mathrm{1}+\mathrm{2}+\centerdot\centerdot\centerdot\right) \\ $$ $$\mathrm{S}=\mathrm{1}+\mathrm{2S} \\ $$ $$\mathrm{S}=−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}} \\ $$ $$\mathrm{this}\:\mathrm{is}\:\mathrm{called}\:\mathrm{analytic}\:\mathrm{continuation} \\ $$ $$\mathrm{its}\:\mathrm{are}\:\mathrm{crazy},\:\mathrm{but}\:\mathrm{cool} \\ $$

Commented byprakash jain last updated on 25/Nov/15

Filup has posted some question earlier as well related to that. Σ_(i=1) ^∞ i=((−1)/(12)) or ζ(−1)=((−1)/(12)) I will read more to see what are the possibilities for ζ function, for example ζ(−2)=Σ_(i=1) ^∞ i^2

$$\mathrm{Filup}\:\mathrm{has}\:\mathrm{posted}\:\mathrm{some}\:\mathrm{question}\:\mathrm{earlier}\:\mathrm{as} \\ $$ $$\mathrm{well}\:\mathrm{related}\:\mathrm{to}\:\mathrm{that}. \\ $$ $$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}=\frac{−\mathrm{1}}{\mathrm{12}}\:\mathrm{or}\:\zeta\left(−\mathrm{1}\right)=\frac{−\mathrm{1}}{\mathrm{12}} \\ $$ $$ \\ $$ $$\mathrm{I}\:\mathrm{will}\:\mathrm{read}\:\mathrm{more}\:\mathrm{to}\:\mathrm{see}\:\mathrm{what}\:\mathrm{are}\:\mathrm{the}\:\mathrm{possibilities} \\ $$ $$\mathrm{for}\:\zeta\:\mathrm{function},\:\mathrm{for}\:\mathrm{example}\:\zeta\left(−\mathrm{2}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{i}^{\mathrm{2}} \\ $$

Commented by123456 last updated on 25/Nov/15

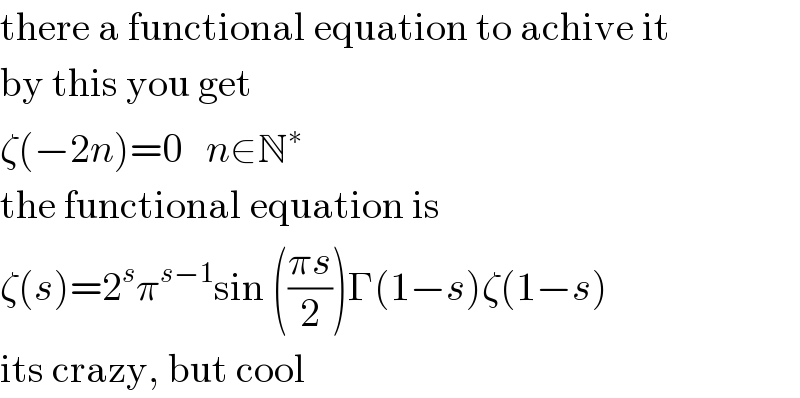
there a functional equation to achive it by this you get ζ(−2n)=0 n∈N^∗ the functional equation is ζ(s)=2^s π^(s−1) sin (((πs)/2))Γ(1−s)ζ(1−s) its crazy, but cool

$$\mathrm{there}\:\mathrm{a}\:\mathrm{functional}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{achive}\:\mathrm{it} \\ $$ $$\mathrm{by}\:\mathrm{this}\:\mathrm{you}\:\mathrm{get} \\ $$ $$\zeta\left(−\mathrm{2}{n}\right)=\mathrm{0}\:\:\:{n}\in\mathbb{N}^{\ast} \\ $$ $$\mathrm{the}\:\mathrm{functional}\:\mathrm{equation}\:\mathrm{is} \\ $$ $$\zeta\left({s}\right)=\mathrm{2}^{{s}} \pi^{{s}−\mathrm{1}} \mathrm{sin}\:\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)\zeta\left(\mathrm{1}−{s}\right) \\ $$ $$\mathrm{its}\:\mathrm{crazy},\:\mathrm{but}\:\mathrm{cool} \\ $$

Commented byFilup last updated on 26/Nov/15

I was incorrect. I have not done the proof I said I did. I mistakenly mixed it up with something else. If someone could make a post on how ζ(−2n)=0, that′d be awsome

$$\mathrm{I}\:\mathrm{was}\:\mathrm{incorrect}.\:\mathrm{I}\:\mathrm{have}\:\mathrm{not}\:\mathrm{done}\:\mathrm{the} \\ $$ $$\mathrm{proof}\:\mathrm{I}\:\mathrm{said}\:\mathrm{I}\:\mathrm{did}.\:\mathrm{I}\:\mathrm{mistakenly}\:\mathrm{mixed}\: \\ $$ $$\mathrm{it}\:\mathrm{up}\:\mathrm{with}\:\mathrm{something}\:\mathrm{else}.\:\mathrm{If}\:\mathrm{someone}\:\mathrm{could} \\ $$ $$\mathrm{make}\:\mathrm{a}\:\mathrm{post}\:\mathrm{on}\:\mathrm{how}\:\zeta\left(−\mathrm{2}{n}\right)=\mathrm{0},\:\mathrm{that}'\mathrm{d} \\ $$ $$\mathrm{be}\:\mathrm{awsome} \\ $$

Commented by123456 last updated on 26/Nov/15

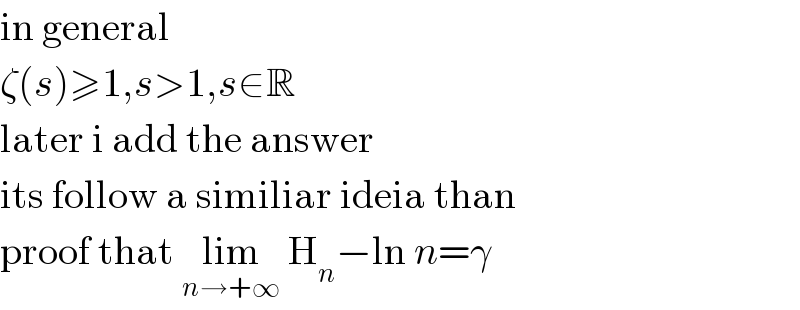
in general ζ(s)≥1,s>1,s∈R later i add the answer its follow a similiar ideia than proof that lim_(n→+∞) H_n −ln n=γ

$$\mathrm{in}\:\mathrm{general} \\ $$ $$\zeta\left({s}\right)\geqslant\mathrm{1},{s}>\mathrm{1},{s}\in\mathbb{R} \\ $$ $$\mathrm{later}\:\mathrm{i}\:\mathrm{add}\:\mathrm{the}\:\mathrm{answer} \\ $$ $$\mathrm{its}\:\mathrm{follow}\:\mathrm{a}\:\mathrm{similiar}\:\mathrm{ideia}\:\mathrm{than} \\ $$ $$\mathrm{proof}\:\mathrm{that}\:\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\mathrm{H}_{{n}} −\mathrm{ln}\:{n}=\gamma \\ $$

Answered by 123456 last updated on 27/Nov/15

x≥1,s>1 ∫_1 ^(+∞) (dx/(⌈x⌉^s ))=Σ_(n=1) ^(+∞) (1/((n+1)^s )) ∫_1 ^(+∞) (dx/(⌊x⌋^s ))=Σ_(n=1) ^(+∞) (1/n^s ) 0<(1/(⌈x⌉^s ))≤(1/x^s )≤(1/(⌊x⌋^s )) (= only for x∈N^∗ ) 0<∫_1 ^(+∞) (dx/(⌈x⌉^s ))<∫_1 ^(+∞) (dx/x^s )<∫_1 ^(+∞) (dx/(⌊x⌋^s )) 0<Σ_(n=1) ^(+∞) (1/((n+1)^s ))<(1/(s−1))<Σ_(n=1) ^(+∞) (1/n^s ) 1<1+Σ_(n=1) ^(+∞) (1/((n+1)^s ))<1+(1/(s−1)) 1<Σ_(n=1) ^(+∞) (1/n^s )<(s/(s−1)) so 1<(1/(s−1))<ζ(s)<(s/(s−1)) (s>1) s→+∞,ζ(s)→1 s→1^+ ,ζ(s)→+∞

$${x}\geqslant\mathrm{1},{s}>\mathrm{1} \\ $$ $$\underset{\mathrm{1}} {\overset{+\infty} {\int}}\frac{{dx}}{\lceil{x}\rceil^{{s}} }=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{s}} } \\ $$ $$\underset{\mathrm{1}} {\overset{+\infty} {\int}}\frac{{dx}}{\lfloor{x}\rfloor^{{s}} }=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} } \\ $$ $$\mathrm{0}<\frac{\mathrm{1}}{\lceil{x}\rceil^{{s}} }\leqslant\frac{\mathrm{1}}{{x}^{{s}} }\leqslant\frac{\mathrm{1}}{\lfloor{x}\rfloor^{{s}} }\:\:\left(=\:\mathrm{only}\:\mathrm{for}\:{x}\in\mathbb{N}^{\ast} \right) \\ $$ $$\mathrm{0}<\underset{\mathrm{1}} {\overset{+\infty} {\int}}\frac{{dx}}{\lceil{x}\rceil^{{s}} }<\underset{\mathrm{1}} {\overset{+\infty} {\int}}\frac{{dx}}{{x}^{{s}} }<\underset{\mathrm{1}} {\overset{+\infty} {\int}}\frac{{dx}}{\lfloor{x}\rfloor^{{s}} } \\ $$ $$\mathrm{0}<\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{s}} }<\frac{\mathrm{1}}{{s}−\mathrm{1}}<\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} } \\ $$ $$\mathrm{1}<\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{s}} }<\mathrm{1}+\frac{\mathrm{1}}{{s}−\mathrm{1}} \\ $$ $$\mathrm{1}<\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} }<\frac{{s}}{{s}−\mathrm{1}} \\ $$ $$\mathrm{so} \\ $$ $$\mathrm{1}<\frac{\mathrm{1}}{{s}−\mathrm{1}}<\zeta\left({s}\right)<\frac{{s}}{{s}−\mathrm{1}}\:\:\:\:\left({s}>\mathrm{1}\right) \\ $$ $${s}\rightarrow+\infty,\zeta\left({s}\right)\rightarrow\mathrm{1} \\ $$ $${s}\rightarrow\mathrm{1}^{+} ,\zeta\left({s}\right)\rightarrow+\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com