Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2705 by Syaka last updated on 25/Nov/15

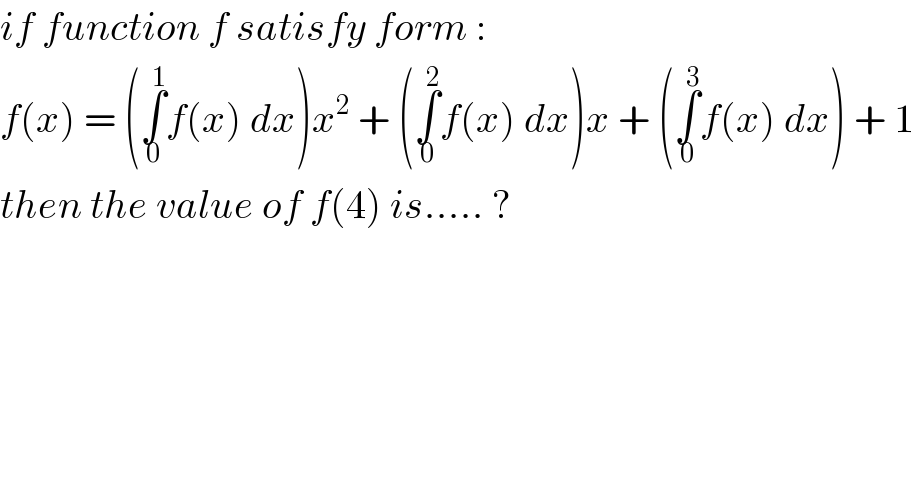
if function f satisfy form : f(x) = (∫_0 ^1 f(x) dx)x^2 + (∫_0 ^2 f(x) dx)x + (∫_0 ^3 f(x) dx) + 1 then the value of f(4) is..... ?

$${if}\:{function}\:{f}\:{satisfy}\:{form}\:: \\ $$$${f}\left({x}\right)\:=\:\left(\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right)\:{dx}\right){x}^{\mathrm{2}} \:+\:\left(\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right)\:{dx}\right){x}\:+\:\left(\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}{f}\left({x}\right)\:{dx}\right)\:+\:\mathrm{1} \\ $$$${then}\:{the}\:{value}\:{of}\:{f}\left(\mathrm{4}\right)\:{is}.....\:? \\ $$

Answered by prakash jain last updated on 25/Nov/15

f(x)=ax^2 +bx+c ....(1) ∫f(x)=a(x^3 /3)+b(x^2 /2)+cx+C ∫_0 ^1 f(x)=(a/3)+(b/2)+c ∫_0 ^2 f(x)=((8a)/3)+2b+2c ∫_0 ^3 f(x)=9a+(9/2)b+3c f(x)= ((a/3)+(b/2)+c)x^2 +(((8a)/3)+2b+2c)x+(9a+(9/2)b+3c)+1 ..(2) Equating coefficients in (1) and (2) (x^2 coeffiient) (a/3)+(b/2)+c=a⇒((2a)/3)=(b/2)+c⇒a=(3/4)b+(3/2)c (x coefficient) ((8a)/3)+2b+2c=b⇒2b+4c+2b+2c=b⇒ 5b=−6c⇒b=((−6c)/5) a=((3b)/4)+((3c)/2)⇒a=−(3/4)×((−6c)/5)+((3c)/2)=((12c)/(20))=((3c)/5) (constant term) (9a+(9/2)b+3c)+1=c To be solved for a, b and c ((27c)/5)−(9/2)×((6c)/5)+2c=−1 c=((−1)/2), a=((−3)/(10)), b=(3/5) f(x)=−(3/(10))x^2 +(3/5)x−(1/2) f(4)=((−3)/(10))×16+(3/5)×4−(1/2)=((−48+24−5)/(10))=((−29)/(10))

$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}\:\:\:\:\:\:\:\:....\left(\mathrm{1}\right) \\ $$$$\int{f}\left({x}\right)={a}\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{b}\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{cx}+{C} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right)=\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+{c} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right)=\frac{\mathrm{8}{a}}{\mathrm{3}}+\mathrm{2}{b}+\mathrm{2}{c} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right)=\mathrm{9}{a}+\frac{\mathrm{9}}{\mathrm{2}}{b}+\mathrm{3}{c} \\ $$$${f}\left({x}\right)= \\ $$$$\left(\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+{c}\right){x}^{\mathrm{2}} +\left(\frac{\mathrm{8}{a}}{\mathrm{3}}+\mathrm{2}{b}+\mathrm{2}{c}\right){x}+\left(\mathrm{9}{a}+\frac{\mathrm{9}}{\mathrm{2}}{b}+\mathrm{3}{c}\right)+\mathrm{1}\:..\left(\mathrm{2}\right) \\ $$$${E}\mathrm{quating}\:\mathrm{coefficients}\:\mathrm{in}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\left({x}^{\mathrm{2}} \:{coeffiient}\right) \\ $$$$\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+{c}={a}\Rightarrow\frac{\mathrm{2}{a}}{\mathrm{3}}=\frac{{b}}{\mathrm{2}}+{c}\Rightarrow{a}=\frac{\mathrm{3}}{\mathrm{4}}{b}+\frac{\mathrm{3}}{\mathrm{2}}{c} \\ $$$$\left({x}\:{coefficient}\right) \\ $$$$\frac{\mathrm{8}{a}}{\mathrm{3}}+\mathrm{2}{b}+\mathrm{2}{c}={b}\Rightarrow\mathrm{2}{b}+\mathrm{4}{c}+\mathrm{2}{b}+\mathrm{2}{c}={b}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}{b}=−\mathrm{6}{c}\Rightarrow{b}=\frac{−\mathrm{6}{c}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\frac{\mathrm{3}{b}}{\mathrm{4}}+\frac{\mathrm{3}{c}}{\mathrm{2}}\Rightarrow{a}=−\frac{\mathrm{3}}{\mathrm{4}}×\frac{−\mathrm{6}{c}}{\mathrm{5}}+\frac{\mathrm{3}{c}}{\mathrm{2}}=\frac{\mathrm{12}{c}}{\mathrm{20}}=\frac{\mathrm{3}{c}}{\mathrm{5}} \\ $$$$\left({constant}\:{term}\right) \\ $$$$\left(\mathrm{9}{a}+\frac{\mathrm{9}}{\mathrm{2}}{b}+\mathrm{3}{c}\right)+\mathrm{1}={c} \\ $$$$\mathrm{To}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:{a},\:{b}\:\mathrm{and}\:{c} \\ $$$$\frac{\mathrm{27}{c}}{\mathrm{5}}−\frac{\mathrm{9}}{\mathrm{2}}×\frac{\mathrm{6}{c}}{\mathrm{5}}+\mathrm{2}{c}=−\mathrm{1} \\ $$$${c}=\frac{−\mathrm{1}}{\mathrm{2}},\:{a}=\frac{−\mathrm{3}}{\mathrm{10}},\:{b}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${f}\left({x}\right)=−\frac{\mathrm{3}}{\mathrm{10}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{5}}{x}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{4}\right)=\frac{−\mathrm{3}}{\mathrm{10}}×\mathrm{16}+\frac{\mathrm{3}}{\mathrm{5}}×\mathrm{4}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{−\mathrm{48}+\mathrm{24}−\mathrm{5}}{\mathrm{10}}=\frac{−\mathrm{29}}{\mathrm{10}} \\ $$

Commented by prakash jain last updated on 25/Nov/15

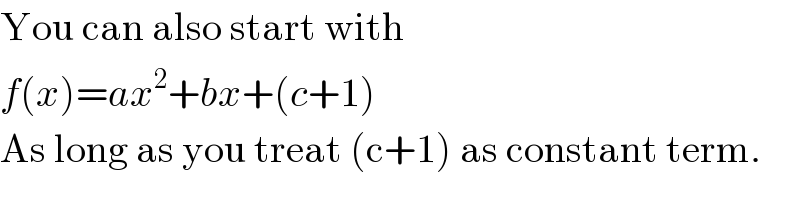
You can also start with f(x)=ax^2 +bx+(c+1) As long as you treat (c+1) as constant term.

$$\mathrm{You}\:\mathrm{can}\:\mathrm{also}\:\mathrm{start}\:\mathrm{with} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+\left({c}+\mathrm{1}\right) \\ $$$$\mathrm{As}\:\mathrm{long}\:\mathrm{as}\:\mathrm{you}\:\mathrm{treat}\:\left(\mathrm{c}+\mathrm{1}\right)\:\mathrm{as}\:\mathrm{constant}\:\mathrm{term}. \\ $$

Commented by Syaka last updated on 25/Nov/15

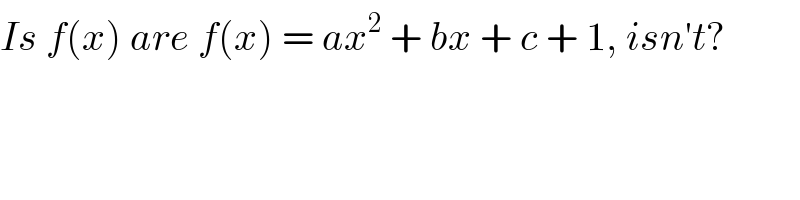
Is f(x) are f(x) = ax^2 + bx + c + 1, isn′t?

$${Is}\:{f}\left({x}\right)\:{are}\:{f}\left({x}\right)\:=\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:+\:\mathrm{1},\:{isn}'{t}? \\ $$

Commented by prakash jain last updated on 25/Nov/15

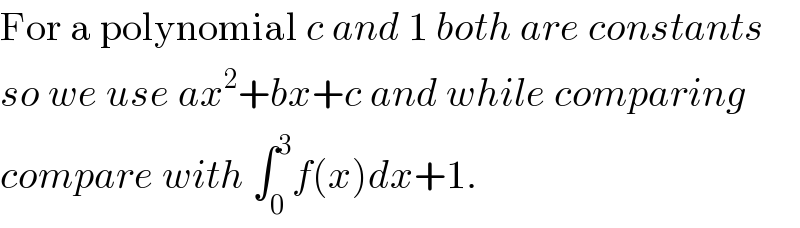
For a polynomial c and 1 both are constants so we use ax^2 +bx+c and while comparing compare with ∫_0 ^3 f(x)dx+1.

$$\mathrm{For}\:\mathrm{a}\:\mathrm{polynomial}\:{c}\:{and}\:\mathrm{1}\:{both}\:{are}\:{constants} \\ $$$${so}\:{we}\:{use}\:{ax}^{\mathrm{2}} +{bx}+{c}\:{and}\:{while}\:{comparing} \\ $$$${compare}\:{with}\:\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}+\mathrm{1}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com