
Question and Answers Forum
Question Number 27182 by abdo imad last updated on 02/Jan/18
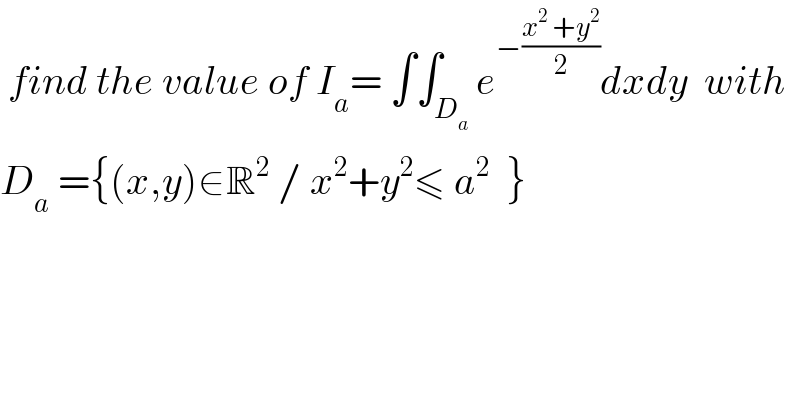
Commented by abdo imad last updated on 05/Jan/18
![we use the polar coordinates and the diffeomorphismeψ (r,θ)−>ψ(r,θ) =(x,y)=(rcosθ,rsinθ) I_(a ) =∫∫_(o≤r≤a) e^(−(r^2 /2)) rdr dθ = ∫_0 ^(2π) ( ∫_0 ^a r e^(−(r^2 /2)) dr )dθ= 2π ∫_0 ^a r e^(−(r^2 /2)) dr = 2π[ − e^(−(r^2 /2)) ]_0 ^a =2π(1− e^(−(a^2 /2)) )](Q27378.png)
| ||
Question and Answers Forum | ||
Question Number 27182 by abdo imad last updated on 02/Jan/18 | ||
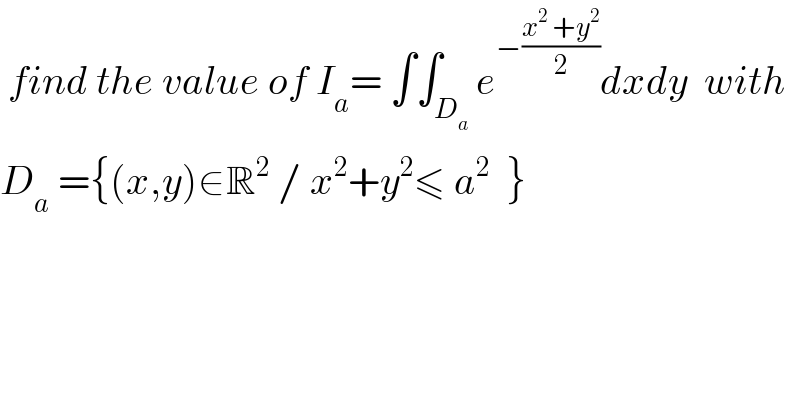 | ||
Commented by abdo imad last updated on 05/Jan/18 | ||
![we use the polar coordinates and the diffeomorphismeψ (r,θ)−>ψ(r,θ) =(x,y)=(rcosθ,rsinθ) I_(a ) =∫∫_(o≤r≤a) e^(−(r^2 /2)) rdr dθ = ∫_0 ^(2π) ( ∫_0 ^a r e^(−(r^2 /2)) dr )dθ= 2π ∫_0 ^a r e^(−(r^2 /2)) dr = 2π[ − e^(−(r^2 /2)) ]_0 ^a =2π(1− e^(−(a^2 /2)) )](Q27378.png) | ||