
Question and Answers Forum
Question Number 27183 by abdo imad last updated on 02/Jan/18
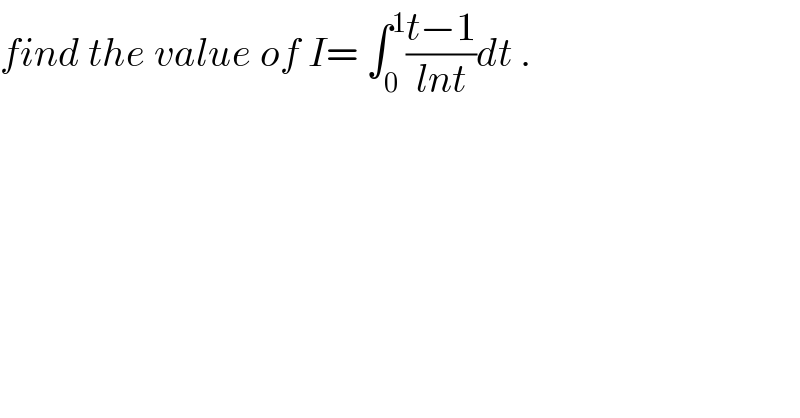
Answered by prakash jain last updated on 03/Jan/18
![F(x)=∫_0 ^1 ((t^x (t−1))/(ln t))dt (dF/dx)=∫_0 ^1 (∂/∂x) (((t^x (t−1))/(ln t)))dt (dF/dx)=∫_0 ^1 ((t^x (t−1))/(ln t))ln t dt (dF/dx)=∫_0 ^1 t^(x+1) −t^x dt=[(t^(x+2) /(x+2))−(t^(x+1) /(x+1))]_0 ^1 =(1/(x+2))−(1/(x+1)) F(x)=ln ∣((x+2)/(x+1))∣+C F(−∞)=0⇒C=0 F(x)=ln ∣((x+2)/(x+1))∣ I=F(0)=ln 2](Q27238.png)
Commented by prakash jain last updated on 03/Jan/18
| ||
Question and Answers Forum | ||
Question Number 27183 by abdo imad last updated on 02/Jan/18 | ||
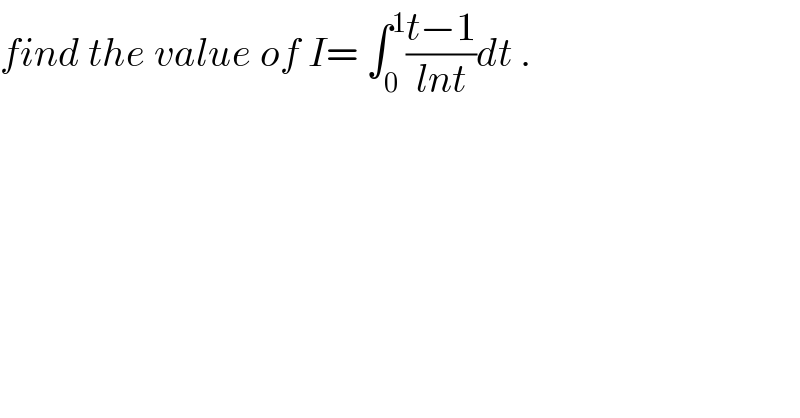 | ||
Answered by prakash jain last updated on 03/Jan/18 | ||
![F(x)=∫_0 ^1 ((t^x (t−1))/(ln t))dt (dF/dx)=∫_0 ^1 (∂/∂x) (((t^x (t−1))/(ln t)))dt (dF/dx)=∫_0 ^1 ((t^x (t−1))/(ln t))ln t dt (dF/dx)=∫_0 ^1 t^(x+1) −t^x dt=[(t^(x+2) /(x+2))−(t^(x+1) /(x+1))]_0 ^1 =(1/(x+2))−(1/(x+1)) F(x)=ln ∣((x+2)/(x+1))∣+C F(−∞)=0⇒C=0 F(x)=ln ∣((x+2)/(x+1))∣ I=F(0)=ln 2](Q27238.png) | ||
| ||
Commented by prakash jain last updated on 03/Jan/18 | ||
 | ||