
Question and Answers Forum
Question Number 27187 by abdo imad last updated on 02/Jan/18
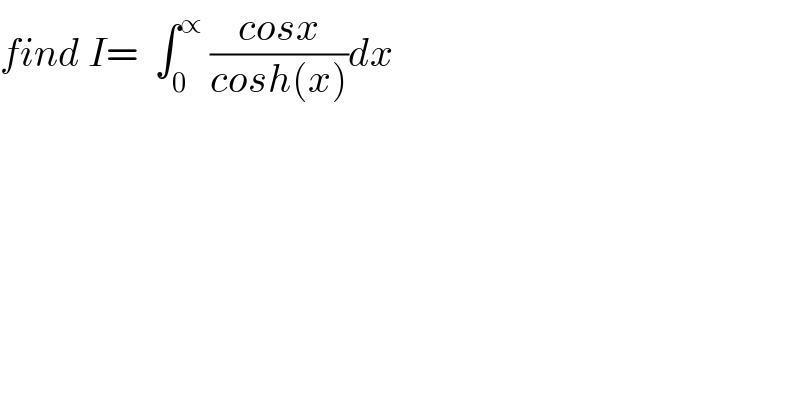
Commented by abdo imad last updated on 08/Jan/18
![I= ∫_0 ^∞ ((cosx)/((e^x +e^(−x) )/2))dx= 2 ∫_0 ^∞ (e^(−x) /(1+e^(−2x) ))cosx dx =2∫_0 ^∞ e^(−x) (Σ_(n=0) ^∝ e^(−2nx) )cosxdx =2 Σ_(n=0) ^∝ ∫_0 ^∞ e^(−(2n+1)x) cosxdx but let calculate ∫_0 ^∞ e^(−ax) cosx dx with a>0 ∫_0 ^∞ e^(−ax) cosx dx= Re (∫_0 ^∞ e^((i−a)x) dx) and ∫_0 ^∞ e^((i−a)x) dx = [ (1/(i−a)) e^((i−a)x) ]_(x=0) ^(x−>∝) = −(1/(i−a))= (1/(a−i)) =((a+i)/(a^2 +1)) ⇒∫_0 ^∞ e^(−ax) cosxdx= (a/(1+a^2 )) so ∫_0 ^∞ e^(−(2n+1)x) cosx dx=((2n+1)/(1+(2n+1)^2 )) I=2Σ_(n=0) ^∝ ((2n+1)/(1+(2n+1)^2 )) and this sum is calculated by fourier series...be continued....](Q27549.png)
| ||
Question and Answers Forum | ||
Question Number 27187 by abdo imad last updated on 02/Jan/18 | ||
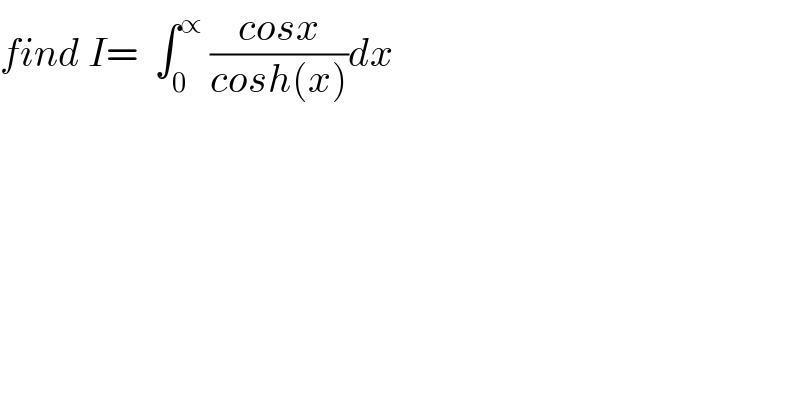 | ||
Commented by abdo imad last updated on 08/Jan/18 | ||
![I= ∫_0 ^∞ ((cosx)/((e^x +e^(−x) )/2))dx= 2 ∫_0 ^∞ (e^(−x) /(1+e^(−2x) ))cosx dx =2∫_0 ^∞ e^(−x) (Σ_(n=0) ^∝ e^(−2nx) )cosxdx =2 Σ_(n=0) ^∝ ∫_0 ^∞ e^(−(2n+1)x) cosxdx but let calculate ∫_0 ^∞ e^(−ax) cosx dx with a>0 ∫_0 ^∞ e^(−ax) cosx dx= Re (∫_0 ^∞ e^((i−a)x) dx) and ∫_0 ^∞ e^((i−a)x) dx = [ (1/(i−a)) e^((i−a)x) ]_(x=0) ^(x−>∝) = −(1/(i−a))= (1/(a−i)) =((a+i)/(a^2 +1)) ⇒∫_0 ^∞ e^(−ax) cosxdx= (a/(1+a^2 )) so ∫_0 ^∞ e^(−(2n+1)x) cosx dx=((2n+1)/(1+(2n+1)^2 )) I=2Σ_(n=0) ^∝ ((2n+1)/(1+(2n+1)^2 )) and this sum is calculated by fourier series...be continued....](Q27549.png) | ||