Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 2720 by prakash jain last updated on 25/Nov/15

Analytical Continuation Sum of the below divergent series was shown to be using analytical continuation. Σ_(i=1) ^n 2^(i−1) =−1 ...(A) ζ(−1)=Σ_(i=0) ^∞ i=−(1/(12)) ...(B) While reading about analytical continuation, I found the found the following: If f_1 is a analytic function over domain D_1 and If f_2 is a analytic function over domain D_2 and f_1 =f_2 on D_1 ∩D_2 , f_2 is called analytical continuation of f_1 and vice versa. Question: In case of series (A) and (B) above what function is used as f_2 to find the sum also what is used as f_1 ?

$$\mathrm{Analytical}\:\mathrm{Continuation} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{below}\:\mathrm{divergent}\:\mathrm{series}\:\mathrm{was} \\ $$$$\mathrm{shown}\:\mathrm{to}\:\mathrm{be}\:\mathrm{using}\:\mathrm{analytical}\:\mathrm{continuation}. \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{i}−\mathrm{1}} =−\mathrm{1}\:\:\:\:\:\:...\left(\mathrm{A}\right) \\ $$$$\zeta\left(−\mathrm{1}\right)=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}{i}=−\frac{\mathrm{1}}{\mathrm{12}}\:\:\:\:\:\:...\left(\mathrm{B}\right) \\ $$$$\mathrm{While}\:\mathrm{reading}\:\mathrm{about}\:\mathrm{analytical}\:\mathrm{continuation}, \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{the}\:\mathrm{found}\:\mathrm{the}\:\mathrm{following}: \\ $$$$\mathrm{If}\:{f}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{function}\:\mathrm{over}\:\mathrm{domain}\:\mathrm{D}_{\mathrm{1}} \:\mathrm{and} \\ $$$$\mathrm{If}\:{f}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{function}\:\mathrm{over}\:\mathrm{domain}\:\mathrm{D}_{\mathrm{2}} \:\mathrm{and} \\ $$$${f}_{\mathrm{1}} ={f}_{\mathrm{2}} \:\mathrm{on}\:\mathrm{D}_{\mathrm{1}} \cap\mathrm{D}_{\mathrm{2}} ,\:{f}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{called}\:\mathrm{analytical}\: \\ $$$$\mathrm{continuation}\:\mathrm{of}\:{f}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{vice}\:\mathrm{versa}. \\ $$$$\boldsymbol{\mathrm{Question}}: \\ $$$$\mathrm{In}\:\mathrm{case}\:\mathrm{of}\:\mathrm{series}\:\left(\mathrm{A}\right)\:\mathrm{and}\:\left(\mathrm{B}\right)\:\mathrm{above}\:\mathrm{what}\:\mathrm{function} \\ $$$$\mathrm{is}\:\mathrm{used}\:\mathrm{as}\:{f}_{\mathrm{2}} \:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{also}\:\mathrm{what}\:\mathrm{is}\:\mathrm{used}\:\mathrm{as}\:{f}_{\mathrm{1}} ? \\ $$

Commented by prakash jain last updated on 25/Nov/15

There is also a question below by Filup about definition of ζ(s) for s<1 using analytical continuity.

$$\mathrm{There}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{question}\:\mathrm{below}\:\mathrm{by}\:\mathrm{Filup}\:\mathrm{about} \\ $$$$\mathrm{definition}\:\mathrm{of}\:\zeta\left({s}\right)\:\mathrm{for}\:{s}<\mathrm{1}\:\mathrm{using}\:\mathrm{analytical} \\ $$$$\mathrm{continuity}. \\ $$

Answered by 123456 last updated on 26/Nov/15

for A f_1 (x)=Σ_(i=0) ^(+∞) x^i f_2 (x)=(1/(1−x)) f_1 (x)=lim_(n→+∞) Σ_(i=0) ^n x^i =lim_(n→+∞) ((x^(n+1) −1)/(x−1)) ∣x∣<1⇒x^(n+1) →0⇒f_1 (x)=((0−1)/(x−1))=(1/(1−x)) f_1 (x)=f_2 (x) ∣x∣<1, so f_2 (x)=(1/(1−x)) is a analytic continuation

$$\mathrm{for}\:\mathrm{A} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{+\infty} {\sum}}{x}^{{i}} \\ $$$${f}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} =\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\mid{x}\mid<\mathrm{1}\Rightarrow{x}^{{n}+\mathrm{1}} \rightarrow\mathrm{0}\Rightarrow{f}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{0}−\mathrm{1}}{{x}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${f}_{\mathrm{1}} \left({x}\right)={f}_{\mathrm{2}} \left({x}\right)\:\mid{x}\mid<\mathrm{1},\:\mathrm{so}\:{f}_{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{analytic}\:\mathrm{continuation} \\ $$

Commented by 123456 last updated on 26/Nov/15

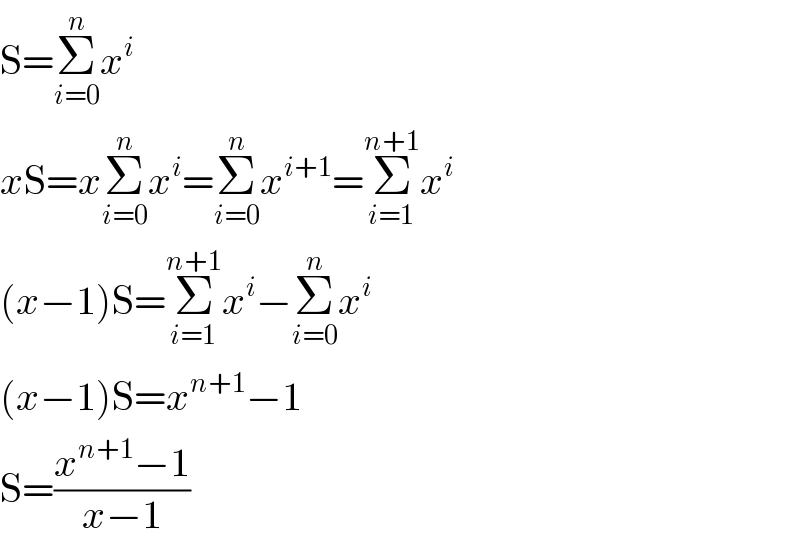
S=Σ_(i=0) ^n x^i xS=xΣ_(i=0) ^n x^i =Σ_(i=0) ^n x^(i+1) =Σ_(i=1) ^(n+1) x^i (x−1)S=Σ_(i=1) ^(n+1) x^i −Σ_(i=0) ^n x^i (x−1)S=x^(n+1) −1 S=((x^(n+1) −1)/(x−1))

$$\mathrm{S}=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} \\ $$$${x}\mathrm{S}={x}\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}+\mathrm{1}} =\underset{{i}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{x}^{{i}} \\ $$$$\left({x}−\mathrm{1}\right)\mathrm{S}=\underset{{i}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{x}^{{i}} −\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{i}} \\ $$$$\left({x}−\mathrm{1}\right)\mathrm{S}={x}^{{n}+\mathrm{1}} −\mathrm{1} \\ $$$$\mathrm{S}=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}} \\ $$

Commented by prakash jain last updated on 26/Nov/15

Thank You.

$$\mathrm{Thank}\:\mathrm{You}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com