Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 27204 by rish@bh last updated on 03/Jan/18

$$\mathrm{if}g\left(x\right)=f\left(x\right)+f(1-x)$$ $$\mathrm{and}{f}^{\left(2\right)}\left(x\right)<0$$ $$\mathrm{then}\mathrm{show}\mathrm{that}$$ $$g\left(x\right)\mathrm{is}\mathrm{increasing}\mathrm{in}(0,1/2)\mathrm{and}$$ $$g\left(x\right)\mathrm{is}\mathrm{decreasing}\mathrm{in}(1/2,1)$$

Answered by Giannibo last updated on 03/Jan/18

$$$$ $$$$ $$\mathrm{\exists }{\mathrm{g}}^{\prime }\mathrm{because}\mathrm{\exists }{\mathrm{f}}^{″}\Rightarrow \mathrm{\exists }{\mathrm{f}}^{\prime }$$ $${\mathrm{g}}^{\prime }\left(\mathrm{x}\right)={\mathrm{f}}^{\prime }\left(\mathrm{x}\right)-{\mathrm{f}}^{\prime }(1-\mathrm{x})$$ $${\mathrm{f}}^{″}\left(\mathrm{x}\right)<0\Rightarrow {\mathrm{f}}^{\prime }\downarrow$$ $$\mathrm{If}\mathrm{x}<1-\mathrm{x}\iff \mathrm{x}<\frac{1}{2}$$ $$\stackrel{{\mathrm{f}}^{\prime }\downarrow }{\Rightarrow }{\mathrm{f}}^{\prime }\left(\mathrm{x}\right)>{\mathrm{f}}^{\prime }(1-\mathrm{x})$$ $${\mathrm{g}}^{\prime }\left(\mathrm{x}\right)>0\Rightarrow \mathrm{g}\uparrow$$ $$$$ $$\mathrm{If}\mathrm{x}>1-\mathrm{x}\iff \mathrm{x}>\frac{1}{2}$$ $$\stackrel{{\mathrm{f}}^{\prime }\downarrow }{\Rightarrow }{\mathrm{f}}^{\prime }\left(\mathrm{x}\right)<{\mathrm{f}}^{\prime }(1-\mathrm{x})$$ $${\mathrm{g}}^{\prime }\left(\mathrm{x}\right)<0\Rightarrow \mathrm{g}\downarrow$$

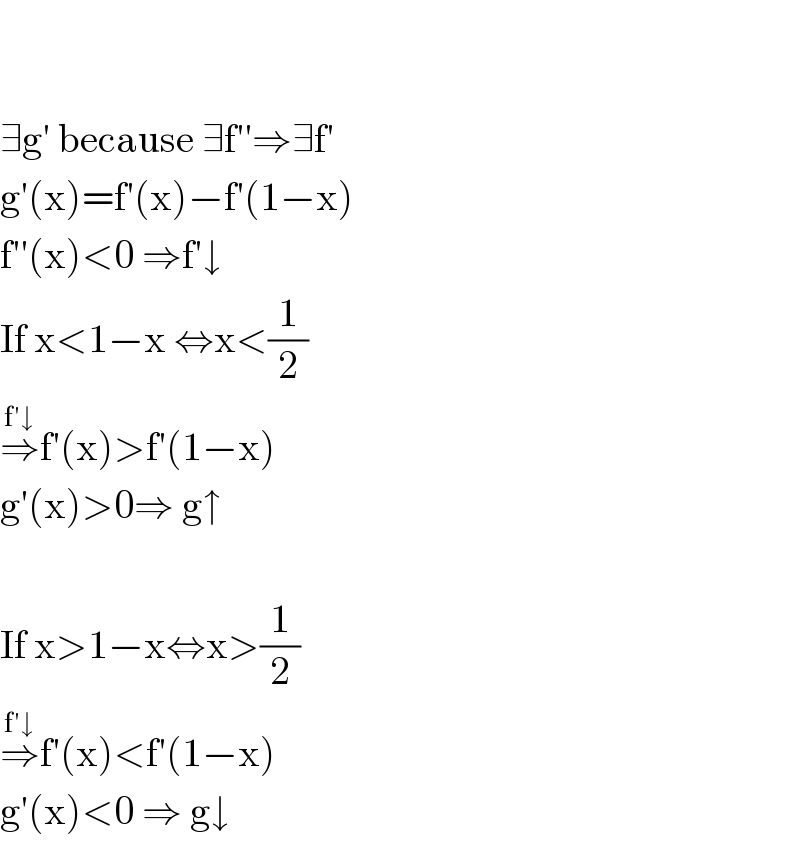
Commented byrish@bh last updated on 03/Jan/18

$$\mathrm{Thank}\mathrm{you}!$$

Commented byPenguin last updated on 04/Jan/18

$$\mathrm{What}\mathrm{does}{f}^{\prime }\downarrow \mathrm{mean}??$$

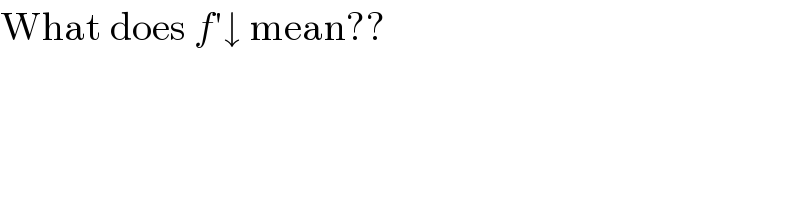
Commented byGiannibo last updated on 04/Jan/18

$${\mathrm{f}}^{\prime }\mathrm{is}\mathrm{decreasing}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com