Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 2722 by prakash jain last updated on 25/Nov/15

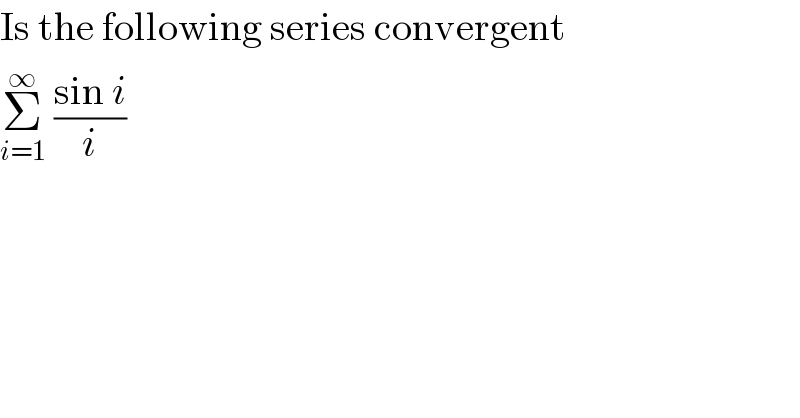
Is the following series convergent Σ_(i=1) ^∞ ((sin i)/i)

$$\mathrm{Is}\:\mathrm{the}\:\mathrm{following}\:\mathrm{series}\:\mathrm{convergent} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{sin}\:{i}}{{i}} \\ $$

Answered by Filup last updated on 25/Nov/15

no for x∈(−∞,∞) −1≤sin x≤1

$$\mathrm{no} \\ $$$$ \\ $$$$\mathrm{for}\:{x}\in\left(−\infty,\infty\right) \\ $$$$−\mathrm{1}\leqslant{sin}\:{x}\leqslant\mathrm{1} \\ $$

Answered by prakash jain last updated on 25/Nov/15

∫_0 ^( ∞) ((sin x)/x) dx=(π/2) ∫_1 ^( ∞) ((sin x)/x) dx=(π/2)−Si(1) As the integral converges, the series is convergent. Update: Wrong test used. The above argument does not prove covergence.

$$\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{sin}\:{x}}{{x}}\:{dx}=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{1}} ^{\:\infty} \:\frac{\mathrm{sin}\:{x}}{{x}}\:{dx}=\frac{\pi}{\mathrm{2}}−\mathrm{Si}\left(\mathrm{1}\right) \\ $$$$\mathrm{As}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{converges},\:\mathrm{the}\:\mathrm{series}\:\mathrm{is} \\ $$$$\mathrm{convergent}. \\ $$$$\mathrm{Update}:\:\mathrm{Wrong}\:\mathrm{test}\:\mathrm{used}.\:\mathrm{The}\:\mathrm{above} \\ $$$$\mathrm{argument}\:\mathrm{does}\:\mathrm{not}\:\mathrm{prove}\:\mathrm{covergence}. \\ $$

Commented by Yozzi last updated on 26/Nov/15

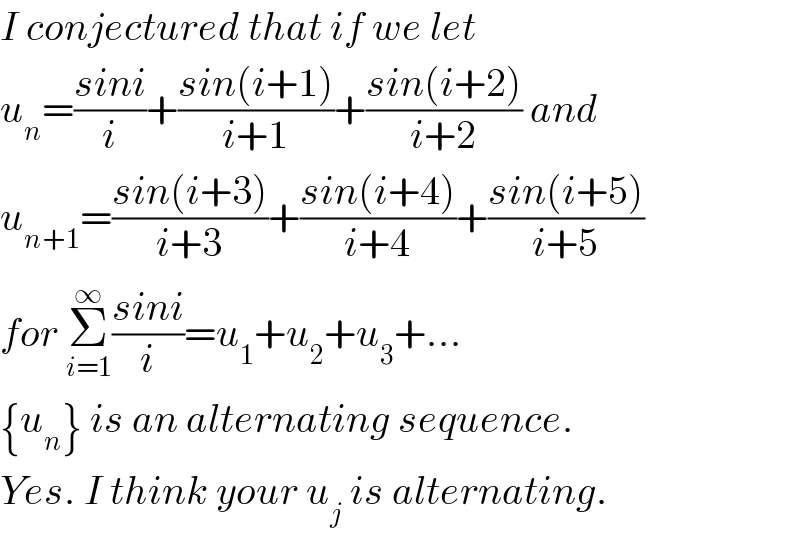
I conjectured that if we let u_n =((sini)/i)+((sin(i+1))/(i+1))+((sin(i+2))/(i+2)) and u_(n+1) =((sin(i+3))/(i+3))+((sin(i+4))/(i+4))+((sin(i+5))/(i+5)) for Σ_(i=1) ^∞ ((sini)/i)=u_1 +u_2 +u_3 +... {u_n } is an alternating sequence. Yes. I think your u_j is alternating.

$${I}\:{conjectured}\:{that}\:{if}\:{we}\:{let} \\ $$$${u}_{{n}} =\frac{{sini}}{{i}}+\frac{{sin}\left({i}+\mathrm{1}\right)}{{i}+\mathrm{1}}+\frac{{sin}\left({i}+\mathrm{2}\right)}{{i}+\mathrm{2}}\:{and}\: \\ $$$${u}_{{n}+\mathrm{1}} =\frac{{sin}\left({i}+\mathrm{3}\right)}{{i}+\mathrm{3}}+\frac{{sin}\left({i}+\mathrm{4}\right)}{{i}+\mathrm{4}}+\frac{{sin}\left({i}+\mathrm{5}\right)}{{i}+\mathrm{5}} \\ $$$${for}\:\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sini}}{{i}}={u}_{\mathrm{1}} +{u}_{\mathrm{2}} +{u}_{\mathrm{3}} +... \\ $$$$\left\{{u}_{{n}} \right\}\:{is}\:{an}\:{alternating}\:{sequence}. \\ $$$${Yes}.\:{I}\:{think}\:{your}\:{u}_{{j}} \:{is}\:{alternating}. \\ $$

Commented by prakash jain last updated on 26/Nov/15

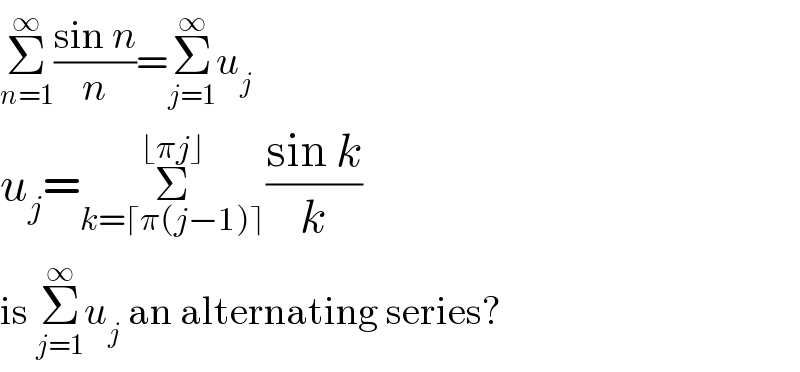
Σ_(n=1) ^∞ ((sin n)/n)=Σ_(j=1) ^∞ u_j u_j =Σ_(k=⌈π(j−1)⌉) ^(⌊πj⌋) ((sin k)/k) is Σ_(j=1) ^∞ u_j an alternating series?

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\:{n}}{{n}}=\underset{{j}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{j}} \\ $$$${u}_{{j}} =\underset{{k}=\lceil\pi\left({j}−\mathrm{1}\right)\rceil} {\overset{\lfloor\pi{j}\rfloor} {\sum}}\frac{\mathrm{sin}\:{k}}{{k}} \\ $$$$\mathrm{is}\:\underset{{j}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{j}} \:\mathrm{an}\:\mathrm{alternating}\:\mathrm{series}? \\ $$

Commented by Filup last updated on 25/Nov/15

My mistake. I Was thinking incorrectly i was thinking of Σ(sin x)

$${My}\:{mistake}.\:\mathrm{I}\:\mathrm{Was}\:\mathrm{thinking} \\ $$$$\mathrm{incorrectly} \\ $$$$\mathrm{i}\:\mathrm{was}\:\mathrm{thinking}\:\mathrm{of}\:\Sigma\left(\mathrm{sin}\:{x}\right) \\ $$

Commented by Yozzi last updated on 25/Nov/15

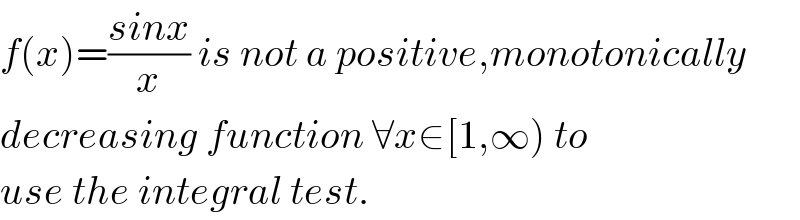
f(x)=((sinx)/x) is not a positive,monotonically decreasing function ∀x∈[1,∞) to use the integral test.

$${f}\left({x}\right)=\frac{{sinx}}{{x}}\:{is}\:{not}\:{a}\:{positive},{monotonically} \\ $$$${decreasing}\:{function}\:\forall{x}\in\left[\mathrm{1},\infty\right)\:{to} \\ $$$${use}\:{the}\:{integral}\:{test}. \\ $$

Commented by prakash jain last updated on 25/Nov/15

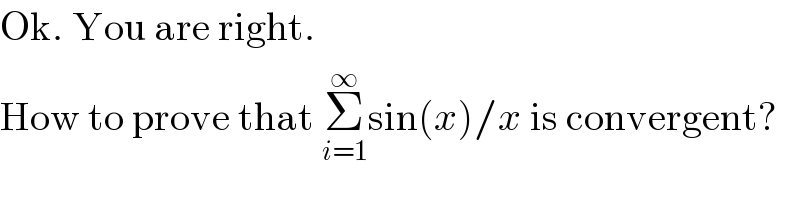
Ok. You are right. How to prove that Σ_(i=1) ^∞ sin(x)/x is convergent?

$$\mathrm{Ok}.\:\mathrm{You}\:\mathrm{are}\:\mathrm{right}. \\ $$$$\mathrm{How}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{sin}\left({x}\right)/{x}\:\mathrm{is}\:\mathrm{convergent}? \\ $$

Commented by Yozzi last updated on 25/Nov/15

Alternating series test: For an infinite series Σ_(n=1) ^∞ u_(n ) of alternating terms the following conditions are required for convergence: (1) ∣u_(n+1) ∣≤∣u_n ∣ for n≥N (2) lim_(n→∞) u_n =0 (or lim_(n→∞) ∣u_n ∣=0)

$${Alternating}\:{series}\:{test}:\: \\ $$$${For}\:{an}\:{infinite}\:{series}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}\:} {of}\:{alternating} \\ $$$${terms}\:{the}\:{following}\:{conditions}\:{are} \\ $$$${required}\:{for}\:{convergence}: \\ $$$$\left(\mathrm{1}\right)\:\mid{u}_{{n}+\mathrm{1}} \mid\leqslant\mid{u}_{{n}} \mid\:{for}\:{n}\geqslant{N} \\ $$$$\left(\mathrm{2}\right)\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{u}_{{n}} =\mathrm{0}\:\left({or}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid{u}_{{n}} \mid=\mathrm{0}\right) \\ $$

Commented by prakash jain last updated on 25/Nov/15

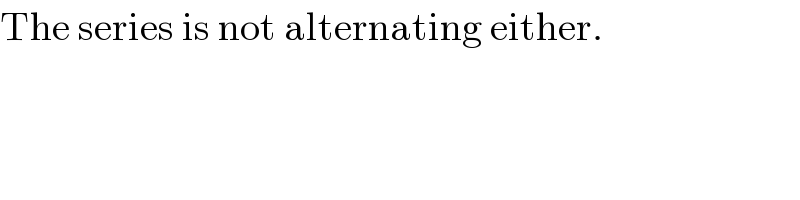
The series is not alternating either.

$$\mathrm{The}\:\mathrm{series}\:\mathrm{is}\:\mathrm{not}\:\mathrm{alternating}\:\mathrm{either}. \\ $$

Commented by Yozzi last updated on 25/Nov/15

true...

$${true}... \\ $$

Commented by prakash jain last updated on 26/Nov/15

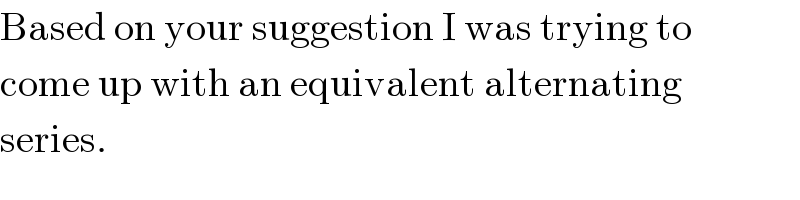
Based on your suggestion I was trying to come up with an equivalent alternating series.

$$\mathrm{Based}\:\mathrm{on}\:\mathrm{your}\:\mathrm{suggestion}\:\mathrm{I}\:\mathrm{was}\:\mathrm{trying}\:\mathrm{to} \\ $$$$\mathrm{come}\:\mathrm{up}\:\mathrm{with}\:\mathrm{an}\:\mathrm{equivalent}\:\mathrm{alternating} \\ $$$$\mathrm{series}. \\ $$

Answered by Yozzi last updated on 26/Nov/15

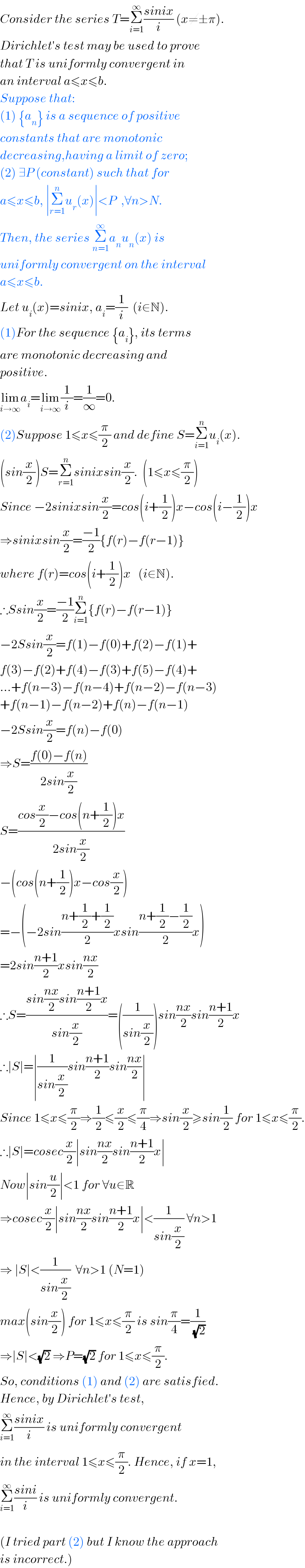
Consider the series T=Σ_(i=1) ^∞ ((sinix)/i) (x≠±π). Dirichlet′s test may be used to prove that T is uniformly convergent in an interval a≤x≤b. Suppose that: (1) {a_n } is a sequence of positive constants that are monotonic decreasing,having a limit of zero; (2) ∃P (constant) such that for a≤x≤b, ∣Σ_(r=1) ^n u_r (x)∣<P ,∀n>N. Then, the series Σ_(n=1) ^∞ a_n u_n (x) is uniformly convergent on the interval a≤x≤b. Let u_i (x)=sinix, a_i =(1/i) (i∈N). (1)For the sequence {a_i }, its terms are monotonic decreasing and positive. lim_(i→∞) a_i =lim_(i→∞) (1/i)=(1/∞)=0. (2)Suppose 1≤x≤(π/2) and define S=Σ_(i=1) ^n u_i (x). (sin(x/2))S=Σ_(r=1) ^n sinixsin(x/2). (1≤x≤(π/2)) Since −2sinixsin(x/2)=cos(i+(1/2))x−cos(i−(1/2))x ⇒sinixsin(x/2)=((−1)/2){f(r)−f(r−1)} where f(r)=cos(i+(1/2))x (i∈N). ∴Ssin(x/2)=((−1)/2)Σ_(i=1) ^n {f(r)−f(r−1)} −2Ssin(x/2)=f(1)−f(0)+f(2)−f(1)+ f(3)−f(2)+f(4)−f(3)+f(5)−f(4)+ ...+f(n−3)−f(n−4)+f(n−2)−f(n−3) +f(n−1)−f(n−2)+f(n)−f(n−1) −2Ssin(x/2)=f(n)−f(0) ⇒S=((f(0)−f(n))/(2sin(x/2))) S=((cos(x/2)−cos(n+(1/2))x)/(2sin(x/2))) −(cos(n+(1/2))x−cos(x/2)) =−(−2sin((n+(1/2)+(1/2))/2)xsin((n+(1/2)−(1/2))/2)x) =2sin((n+1)/2)xsin((nx)/2) ∴S=((sin((nx)/2)sin((n+1)/2)x)/(sin(x/2)))=((1/(sin(x/2))))sin((nx)/2)sin((n+1)/2)x ∴∣S∣=∣(1/(sin(x/2)))sin((n+1)/2)sin((nx)/2)∣ Since 1≤x≤(π/2)⇒(1/2)≤(x/2)≤(π/4)⇒sin(x/2)≥sin(1/2) for 1≤x≤(π/2). ∴∣S∣=cosec(x/2)∣sin((nx)/2)sin((n+1)/2)x∣ Now∣sin(u/2)∣<1 for ∀u∈R ⇒cosec(x/2)∣sin((nx)/2)sin((n+1)/2)x∣<(1/(sin(x/2))) ∀n>1 ⇒ ∣S∣<(1/(sin(x/2))) ∀n>1 (N=1) max(sin(x/2)) for 1≤x≤(π/2) is sin(π/4)=(1/(√2)) ⇒∣S∣<(√2) ⇒P=(√2) for 1≤x≤(π/2). So, conditions (1) and (2) are satisfied. Hence, by Dirichlet′s test, Σ_(i=1) ^∞ ((sinix)/i) is uniformly convergent in the interval 1≤x≤(π/2). Hence, if x=1, Σ_(i=1) ^∞ ((sini)/i) is uniformly convergent. (I tried part (2) but I know the approach is incorrect.)

$${Consider}\:{the}\:{series}\:{T}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sinix}}{{i}}\:\left({x}\neq\pm\pi\right). \\ $$$${Dirichlet}'{s}\:{test}\:{may}\:{be}\:{used}\:{to}\:{prove} \\ $$$${that}\:{T}\:{is}\:{uniformly}\:{convergent}\:{in} \\ $$$${an}\:{interval}\:{a}\leqslant{x}\leqslant{b}. \\ $$$${Suppose}\:{that}: \\ $$$$\left(\mathrm{1}\right)\:\left\{{a}_{{n}} \right\}\:{is}\:{a}\:{sequence}\:{of}\:{positive}\: \\ $$$${constants}\:{that}\:{are}\:{monotonic} \\ $$$${decreasing},{having}\:{a}\:{limit}\:{of}\:{zero}; \\ $$$$\left(\mathrm{2}\right)\:\exists{P}\:\left({constant}\right)\:{such}\:{that}\:{for} \\ $$$${a}\leqslant{x}\leqslant{b},\:\mid\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{r}} \left({x}\right)\mid<{P}\:\:,\forall{n}>{N}. \\ $$$${Then},\:{the}\:{series}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{a}_{{n}} {u}_{{n}} \left({x}\right)\:{is}\: \\ $$$${uniformly}\:{convergent}\:{on}\:{the}\:{interval} \\ $$$${a}\leqslant{x}\leqslant{b}. \\ $$$${Let}\:{u}_{{i}} \left({x}\right)={sinix},\:{a}_{{i}} =\frac{\mathrm{1}}{{i}}\:\:\left({i}\in\mathbb{N}\right). \\ $$$$\left(\mathrm{1}\right){For}\:{the}\:{sequence}\:\left\{{a}_{{i}} \right\},\:{its}\:{terms}\: \\ $$$${are}\:{monotonic}\:{decreasing}\:{and} \\ $$$${positive}. \\ $$$$\underset{{i}\rightarrow\infty} {\mathrm{lim}}{a}_{{i}} =\underset{{i}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{i}}=\frac{\mathrm{1}}{\infty}=\mathrm{0}. \\ $$$$\left(\mathrm{2}\right){Suppose}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\:{and}\:{define}\:{S}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{i}} \left({x}\right). \\ $$$$\left({sin}\frac{{x}}{\mathrm{2}}\right){S}=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{sinixsin}\frac{{x}}{\mathrm{2}}.\:\:\left(\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\right) \\ $$$${Since}\:−\mathrm{2}{sinixsin}\frac{{x}}{\mathrm{2}}={cos}\left({i}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({i}−\frac{\mathrm{1}}{\mathrm{2}}\right){x} \\ $$$$\Rightarrow{sinixsin}\frac{{x}}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}}\left\{{f}\left({r}\right)−{f}\left({r}−\mathrm{1}\right)\right\} \\ $$$${where}\:{f}\left({r}\right)={cos}\left({i}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}\:\:\:\left({i}\in\mathbb{N}\right). \\ $$$$\therefore{Ssin}\frac{{x}}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{{f}\left({r}\right)−{f}\left({r}−\mathrm{1}\right)\right\} \\ $$$$−\mathrm{2}{Ssin}\frac{{x}}{\mathrm{2}}={f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{2}\right)−{f}\left(\mathrm{1}\right)+ \\ $$$${f}\left(\mathrm{3}\right)−{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{4}\right)−{f}\left(\mathrm{3}\right)+{f}\left(\mathrm{5}\right)−{f}\left(\mathrm{4}\right)+ \\ $$$$...+{f}\left({n}−\mathrm{3}\right)−{f}\left({n}−\mathrm{4}\right)+{f}\left({n}−\mathrm{2}\right)−{f}\left({n}−\mathrm{3}\right) \\ $$$$+{f}\left({n}−\mathrm{1}\right)−{f}\left({n}−\mathrm{2}\right)+{f}\left({n}\right)−{f}\left({n}−\mathrm{1}\right) \\ $$$$−\mathrm{2}{Ssin}\frac{{x}}{\mathrm{2}}={f}\left({n}\right)−{f}\left(\mathrm{0}\right) \\ $$$$\Rightarrow{S}=\frac{{f}\left(\mathrm{0}\right)−{f}\left({n}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$${S}=\frac{{cos}\frac{{x}}{\mathrm{2}}−{cos}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$−\left({cos}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\frac{{x}}{\mathrm{2}}\right) \\ $$$$=−\left(−\mathrm{2}{sin}\frac{{n}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}{xsin}\frac{{n}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}{x}\right) \\ $$$$=\mathrm{2}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{xsin}\frac{{nx}}{\mathrm{2}} \\ $$$$\therefore{S}=\frac{{sin}\frac{{nx}}{\mathrm{2}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}}{{sin}\frac{{x}}{\mathrm{2}}}=\left(\frac{\mathrm{1}}{{sin}\frac{{x}}{\mathrm{2}}}\right){sin}\frac{{nx}}{\mathrm{2}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{x} \\ $$$$\therefore\mid{S}\mid=\mid\frac{\mathrm{1}}{{sin}\frac{{x}}{\mathrm{2}}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{sin}\frac{{nx}}{\mathrm{2}}\mid \\ $$$${Since}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{{x}}{\mathrm{2}}\leqslant\frac{\pi}{\mathrm{4}}\Rightarrow{sin}\frac{{x}}{\mathrm{2}}\geqslant{sin}\frac{\mathrm{1}}{\mathrm{2}}\:{for}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}. \\ $$$$\therefore\mid{S}\mid={cosec}\frac{{x}}{\mathrm{2}}\mid{sin}\frac{{nx}}{\mathrm{2}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\mid \\ $$$${Now}\mid{sin}\frac{{u}}{\mathrm{2}}\mid<\mathrm{1}\:{for}\:\forall{u}\in\mathbb{R} \\ $$$$\Rightarrow{cosec}\frac{{x}}{\mathrm{2}}\mid{sin}\frac{{nx}}{\mathrm{2}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\mid<\frac{\mathrm{1}}{{sin}\frac{{x}}{\mathrm{2}}}\:\forall{n}>\mathrm{1} \\ $$$$\Rightarrow\:\mid{S}\mid<\frac{\mathrm{1}}{{sin}\frac{{x}}{\mathrm{2}}}\:\:\forall{n}>\mathrm{1}\:\left({N}=\mathrm{1}\right) \\ $$$${max}\left({sin}\frac{{x}}{\mathrm{2}}\right)\:{for}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\:{is}\:{sin}\frac{\pi}{\mathrm{4}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mid{S}\mid<\sqrt{\mathrm{2}}\:\Rightarrow{P}=\sqrt{\mathrm{2}}\:{for}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}. \\ $$$${So},\:{conditions}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:{are}\:{satisfied}. \\ $$$${Hence},\:{by}\:{Dirichlet}'{s}\:{test}, \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sinix}}{{i}}\:{is}\:{uniformly}\:{convergent} \\ $$$${in}\:{the}\:{interval}\:\mathrm{1}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}.\:{Hence},\:{if}\:{x}=\mathrm{1}, \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sini}}{{i}}\:{is}\:{uniformly}\:{convergent}. \\ $$$$ \\ $$$$\left({I}\:{tried}\:{part}\:\left(\mathrm{2}\right)\:{but}\:{I}\:{know}\:{the}\:{approach}\right. \\ $$$$\left.{is}\:{incorrect}.\right) \\ $$

Commented by prakash jain last updated on 26/Nov/15

Innovative! The series in question could start with sinisin 0.5 (x=1). However you have proved more generic case. Your approach looks correct to me. Why do you think it is wrong?

$$\mathrm{Innovative}! \\ $$$$\mathrm{The}\:\mathrm{series}\:\mathrm{in}\:\mathrm{question}\:\mathrm{could}\:\mathrm{start} \\ $$$$\mathrm{with}\:\mathrm{sin}{i}\mathrm{sin}\:\mathrm{0}.\mathrm{5}\:\left({x}=\mathrm{1}\right). \\ $$$$\mathrm{However}\:\mathrm{you}\:\mathrm{have}\:\mathrm{proved}\:\mathrm{more}\:\mathrm{generic}\:\mathrm{case}. \\ $$$$\mathrm{Your}\:\mathrm{approach}\:\mathrm{looks}\:\mathrm{correct}\:\mathrm{to}\:\mathrm{me}. \\ $$$$\mathrm{Why}\:\mathrm{do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{wrong}? \\ $$

Commented by Yozzi last updated on 26/Nov/15

This area is new to me and I haven′t mastered method of proof yet. But I′m glad you see no issues with it :).

$${This}\:{area}\:{is}\:{new}\:{to}\:{me}\:{and}\:{I}\:{haven}'{t} \\ $$$${mastered}\:{method}\:{of}\:{proof}\:{yet}.\:{But} \\ $$$$\left.{I}'{m}\:{glad}\:{you}\:{see}\:{no}\:{issues}\:{with}\:{it}\::\right). \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com