
Question and Answers Forum
Question Number 27280 by kemhoney78@gmail.com last updated on 04/Jan/18
![If for a real number y, [y] is the greatest integer less than or equal to y, then the value of the integeral ∫_(π/2) ^(3π/2) [2 sin x]dx is](Q27280.png)
Commented by abdo imad last updated on 04/Jan/18
![let do the changement x= (π/2) +t ∫_(π/2) ^((3π)/2) [2sinx]dx= ∫_0 ^π [2 cosx]dx ( 2cosx=t ⇔ x =arcos((t/2)))= =∫_2 ^(−2) [t](−(1/(2(√(1−(t^2 /4))))))dt= (1/2) ∫_(−2) ^2 (([t])/(√(1−(t^2 /4)))) dt =(1/2) ∫_(−2) ^(−1) (...)dt +(1/2) ∫_(−1) ^0 (...)dt +(1/2) ∫_0 ^1 (...)dt +(1/2) ∫_1 ^2 (...)dt =−∫_(−2) ^(−1 ) (dt/(√(1−(t^2 /4)))) −(1/2) ∫_(−1) ^0 (dt/(√(1−(t^2 /4)))) +0+(1/2)∫_1 ^2 (dt/(√(1−(t^2 /4))))dt =−∫_2 ^1 ((−dt)/(√(1−(t^2 /4)))) +(1/2)∫_1 ^(2 ) (dt/(√(1−(t^2 /4)))) −(1/2) ∫_1 ^0 ((−dt)/(√(1−(t^2 /4)))) =−∫_1 ^2 (dt/(√(1−(t^2 /4)))) +(1/2) ∫_1 ^2 (dt/(√(1−(t^2 /2)))) −(1/2) ∫_0 ^1 (dt/(√(1−(t^2 /4)))) =−(1/2) ∫_1 ^2 (dt/(√(1−(t^2 /2)))) −(1/2) ∫_0 ^1 (dt/(√(1−(t^2 /4))))dt =−(1/2) ∫_0 ^2 (dt/(√(1−(t^2 /4)))) dt=[ arcos((t/2))]_0 ^2 =arcos(1)−arcos0= −(π/2)](Q27292.png)
Answered by ajfour last updated on 04/Jan/18
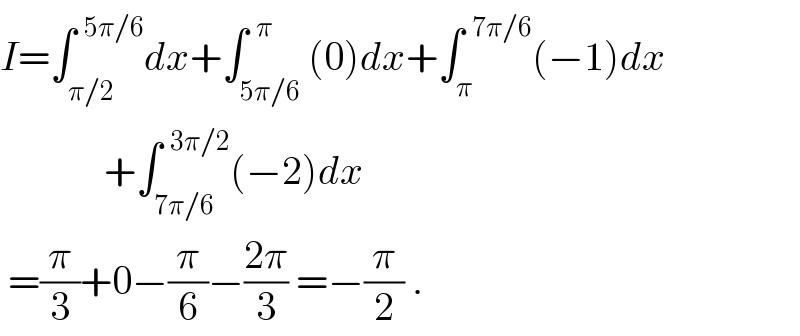
Commented by ajfour last updated on 04/Jan/18

| ||
Question and Answers Forum | ||
Question Number 27280 by kemhoney78@gmail.com last updated on 04/Jan/18 | ||
![If for a real number y, [y] is the greatest integer less than or equal to y, then the value of the integeral ∫_(π/2) ^(3π/2) [2 sin x]dx is](Q27280.png) | ||
Commented by abdo imad last updated on 04/Jan/18 | ||
![let do the changement x= (π/2) +t ∫_(π/2) ^((3π)/2) [2sinx]dx= ∫_0 ^π [2 cosx]dx ( 2cosx=t ⇔ x =arcos((t/2)))= =∫_2 ^(−2) [t](−(1/(2(√(1−(t^2 /4))))))dt= (1/2) ∫_(−2) ^2 (([t])/(√(1−(t^2 /4)))) dt =(1/2) ∫_(−2) ^(−1) (...)dt +(1/2) ∫_(−1) ^0 (...)dt +(1/2) ∫_0 ^1 (...)dt +(1/2) ∫_1 ^2 (...)dt =−∫_(−2) ^(−1 ) (dt/(√(1−(t^2 /4)))) −(1/2) ∫_(−1) ^0 (dt/(√(1−(t^2 /4)))) +0+(1/2)∫_1 ^2 (dt/(√(1−(t^2 /4))))dt =−∫_2 ^1 ((−dt)/(√(1−(t^2 /4)))) +(1/2)∫_1 ^(2 ) (dt/(√(1−(t^2 /4)))) −(1/2) ∫_1 ^0 ((−dt)/(√(1−(t^2 /4)))) =−∫_1 ^2 (dt/(√(1−(t^2 /4)))) +(1/2) ∫_1 ^2 (dt/(√(1−(t^2 /2)))) −(1/2) ∫_0 ^1 (dt/(√(1−(t^2 /4)))) =−(1/2) ∫_1 ^2 (dt/(√(1−(t^2 /2)))) −(1/2) ∫_0 ^1 (dt/(√(1−(t^2 /4))))dt =−(1/2) ∫_0 ^2 (dt/(√(1−(t^2 /4)))) dt=[ arcos((t/2))]_0 ^2 =arcos(1)−arcos0= −(π/2)](Q27292.png) | ||
Answered by ajfour last updated on 04/Jan/18 | ||
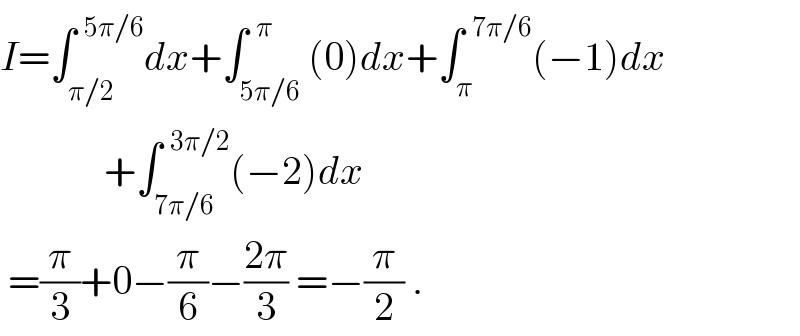 | ||
| ||
Commented by ajfour last updated on 04/Jan/18 | ||
 | ||