
Question and Answers Forum
Question Number 27294 by iy last updated on 04/Jan/18
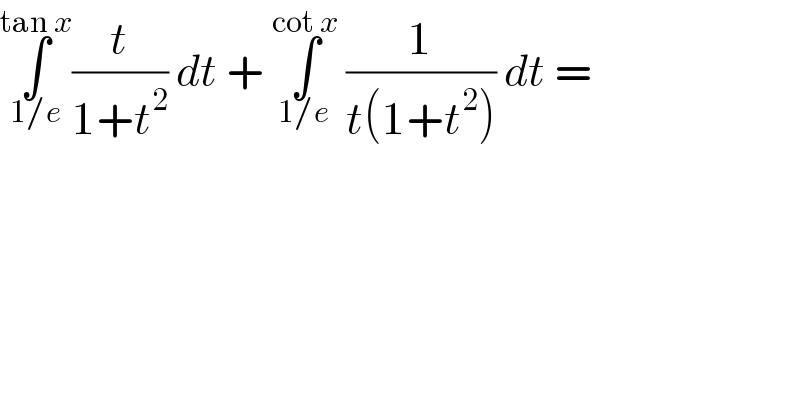
Commented by prakash jain last updated on 05/Jan/18
![(A) ∫_(1/e) ^(tan x) (t/(1+t^2 ))dt=(1/2)[ln (1+tan^2 x)−ln (1+(1/e^2 ))] =(1/2)[ln (sec^2 x)−ln (1+(1/e^2 ))] =ln (secx)−(1/2)ln (1+(1/e^2 )) ∫_(1/e) ^(cot x) (1/(t(1+t^2 )))dt ∫_(1/e) ^(cot x) ((t/t^2 )−(t/(1+t^2 )))dt =[ln t−(1/2)ln (1+t^2 )]_(1/e) ^(cot x) (B) =ln cot x−(1/2)ln (1+cot^2 x)−ln (1/e)+(1/2)ln (1+(1/e^2 )) =ln cot x−ln cosec x−ln (1/e)+(1/2)ln (1+(1/e^2 )) A+B ln sec x+ln cot x−ln cosec x+1 =ln (sec x∙cot x)−ln cosec x+1 =ln cosec x−ln cosec x+1 =1](Q27372.png)
| ||
Question and Answers Forum | ||
Question Number 27294 by iy last updated on 04/Jan/18 | ||
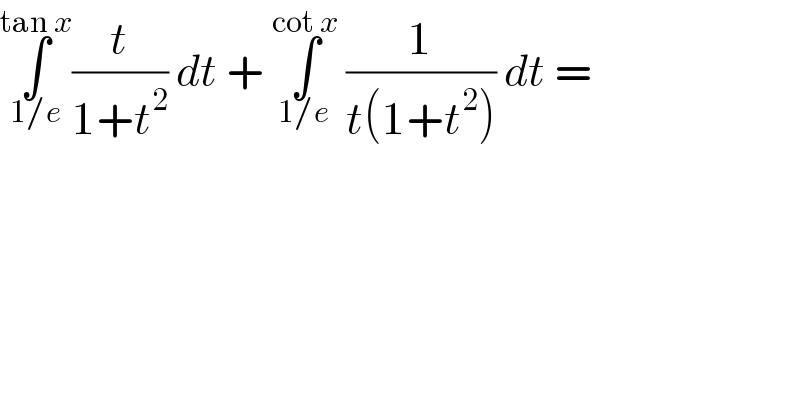 | ||
Commented by prakash jain last updated on 05/Jan/18 | ||
![(A) ∫_(1/e) ^(tan x) (t/(1+t^2 ))dt=(1/2)[ln (1+tan^2 x)−ln (1+(1/e^2 ))] =(1/2)[ln (sec^2 x)−ln (1+(1/e^2 ))] =ln (secx)−(1/2)ln (1+(1/e^2 )) ∫_(1/e) ^(cot x) (1/(t(1+t^2 )))dt ∫_(1/e) ^(cot x) ((t/t^2 )−(t/(1+t^2 )))dt =[ln t−(1/2)ln (1+t^2 )]_(1/e) ^(cot x) (B) =ln cot x−(1/2)ln (1+cot^2 x)−ln (1/e)+(1/2)ln (1+(1/e^2 )) =ln cot x−ln cosec x−ln (1/e)+(1/2)ln (1+(1/e^2 )) A+B ln sec x+ln cot x−ln cosec x+1 =ln (sec x∙cot x)−ln cosec x+1 =ln cosec x−ln cosec x+1 =1](Q27372.png) | ||