
Question and Answers Forum
Question Number 57138 by mustakim420 last updated on 30/Mar/19
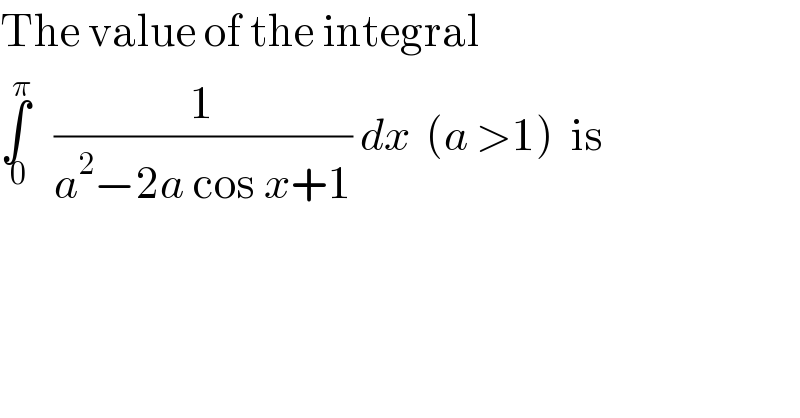
Commented bymaxmathsup by imad last updated on 30/Mar/19
![let f(a) =∫_0 ^π (dx/(a^2 −2acosx +1)) ⇒f(a) =_(tan((x/2))=t) ∫_0 ^(+∞) ((2dt)/((1+t^2 )(a^2 −2a((1−t^2 )/(1+t^2 )) +1))) =2 ∫_0 ^∞ (dt/((1+t^2 )a^2 −2a(1−t^2 )+1+t^2 )) =2 ∫_0 ^∞ (dt/(a^2 t^2 +a^2 −2a+2at^2 +1+t^2 )) =2 ∫_0 ^∞ (dt/((a^2 +2a+1)t^(2 ) +a^2 −2a+1)) =2 ∫_0 ^∞ (dt/((a+1)^2 t^2 +(a−1)^2 )) changement (a+1)t =(a−1)u give f(a) =2 ∫_0 ^∞ (1/((a−1)^2 (1+u^2 ))) ((a−1)/(a+1)) du =(2/(a^2 −1)) [arctan(u)]_0 ^(+∞) =(2/(a^2 −1)) (π/2) =(π/(a^2 −1)) ⇒f(a) =(π/(a^2 −1)) with a>1 .](Q57156.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19
![∫(dx/(a^2 +1−2acosx)) (1/(2a))∫(dx/(k−cosx)) [k=((a^2 +1)/(2a))] t=tan(x/2) 2dt=sec^2 (x/2)dx dx=((2dt)/(1+t^2 )) (1/(2a))∫((2dt)/((1+t^2 )(k−((1−t^2 )/(1+t^2 ))))) (1/a)∫(dt/(k+kt^2 −1+t^2 )) (1/a)∫(dt/((k−1)+t^2 (k+1))) (1/(a(k+1)))∫(dt/(((k−1)/(k+1))+t^2 )) (1/(a(((a^2 +1)/(2a))+1)))×(1/(√((k−1)/(k+1))))tan^(−1) ((t/(√((k−1)/(k+1))))) k=((a^2 +1)/(2a)) ((k−1)/(k+1))=((a^2 +1+2a)/(a^2 +1−2a))=(((a+1)^2 )/((a−1)^2 )) (√((k−1)/(k+1))) =((a+1)/(a−1)) (2/((a+1)^2 ))×(1/((a−1)/(a+1)))∣tan^(−1) (((tan(x/2))/((a−1)/(a+1))))∣_0 ^π (2/(a^2 −1))×[tan^(−1) (∞)−0] (2/(a^2 −1))×(π/2)→(π/(a^2 −1))](Q57145.png)
| ||
Question and Answers Forum | ||
Question Number 57138 by mustakim420 last updated on 30/Mar/19 | ||
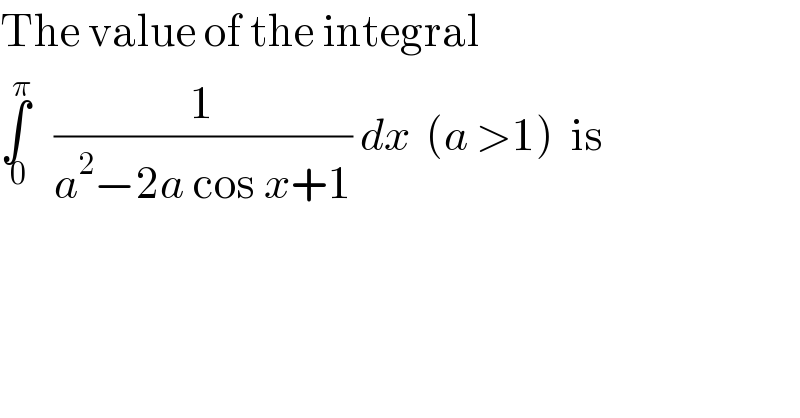 | ||
Commented bymaxmathsup by imad last updated on 30/Mar/19 | ||
![let f(a) =∫_0 ^π (dx/(a^2 −2acosx +1)) ⇒f(a) =_(tan((x/2))=t) ∫_0 ^(+∞) ((2dt)/((1+t^2 )(a^2 −2a((1−t^2 )/(1+t^2 )) +1))) =2 ∫_0 ^∞ (dt/((1+t^2 )a^2 −2a(1−t^2 )+1+t^2 )) =2 ∫_0 ^∞ (dt/(a^2 t^2 +a^2 −2a+2at^2 +1+t^2 )) =2 ∫_0 ^∞ (dt/((a^2 +2a+1)t^(2 ) +a^2 −2a+1)) =2 ∫_0 ^∞ (dt/((a+1)^2 t^2 +(a−1)^2 )) changement (a+1)t =(a−1)u give f(a) =2 ∫_0 ^∞ (1/((a−1)^2 (1+u^2 ))) ((a−1)/(a+1)) du =(2/(a^2 −1)) [arctan(u)]_0 ^(+∞) =(2/(a^2 −1)) (π/2) =(π/(a^2 −1)) ⇒f(a) =(π/(a^2 −1)) with a>1 .](Q57156.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19 | ||
![∫(dx/(a^2 +1−2acosx)) (1/(2a))∫(dx/(k−cosx)) [k=((a^2 +1)/(2a))] t=tan(x/2) 2dt=sec^2 (x/2)dx dx=((2dt)/(1+t^2 )) (1/(2a))∫((2dt)/((1+t^2 )(k−((1−t^2 )/(1+t^2 ))))) (1/a)∫(dt/(k+kt^2 −1+t^2 )) (1/a)∫(dt/((k−1)+t^2 (k+1))) (1/(a(k+1)))∫(dt/(((k−1)/(k+1))+t^2 )) (1/(a(((a^2 +1)/(2a))+1)))×(1/(√((k−1)/(k+1))))tan^(−1) ((t/(√((k−1)/(k+1))))) k=((a^2 +1)/(2a)) ((k−1)/(k+1))=((a^2 +1+2a)/(a^2 +1−2a))=(((a+1)^2 )/((a−1)^2 )) (√((k−1)/(k+1))) =((a+1)/(a−1)) (2/((a+1)^2 ))×(1/((a−1)/(a+1)))∣tan^(−1) (((tan(x/2))/((a−1)/(a+1))))∣_0 ^π (2/(a^2 −1))×[tan^(−1) (∞)−0] (2/(a^2 −1))×(π/2)→(π/(a^2 −1))](Q57145.png) | ||
| ||