Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 27303 by Tinkutara last updated on 04/Jan/18

Answered by mrW1 last updated on 05/Jan/18

$$a=a_{//}=\frac{g}{2}\left(given\right)$$$$a_{\mathrm{\perp }}=a\sin \theta =\frac{g\sin \theta }{2}$$$$mg\cos \theta -N={ma}_{\mathrm{\perp }}=\frac{mg\sin \theta }{2}$$$$\Rightarrow N=mg(\cos \theta -\frac{\sin \theta }{2})=mg(\frac{4}{5}-\frac{3}{2\times 5})=\frac{mg}{2}$$

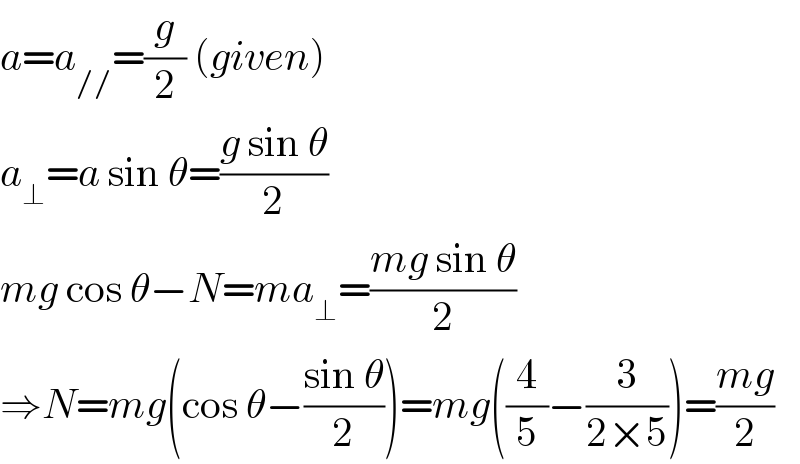
Commented by mrW1 last updated on 05/Jan/18

Commented by Tinkutara last updated on 05/Jan/18

$$Why{a}_{\mathrm{\perp }}=a\sin \theta ?$$

Commented by mrW1 last updated on 05/Jan/18

$$thecomponentofafromMindirectionnormal$$$$tothecontactsurfaceisa\sin \theta ,which$$$$mustbethesameas{a}_{\mathrm{\perp }}fromm.$$

Commented by mrW1 last updated on 05/Jan/18

Commented by mrW1 last updated on 05/Jan/18

$$letx=displacementofwedgeM$$$$accelerationofblockMisa=\frac{d^{2}x}{{dt}^2}$$$$displacementofblockmis$$$$s_{//}=x$$$$s_{\mathrm{\perp }}=x\sin \theta$$$$\Rightarrow a_{//}=\frac{d^2{s}_{//}}{{dt}^2}=a$$$$\Rightarrow a_{\mathrm{\perp }}=\frac{d^2{s}_{\mathrm{\perp }}}{{dt}^2}=a\sin \theta$$

Commented by Tinkutara last updated on 05/Jan/18

Then why the relative acceleration of block is g/2 w.r.t wedge?

Commented by mrW1 last updated on 05/Jan/18

$$itisgiventhat{a}_{//}=\frac{g}{2}.infactitis$$$$dependentonthemassofthewedge.$$$$IthinkifM=\frac{16}{25}m{we}^{\prime }llget{a}_{//}=\frac{g}{2}.$$

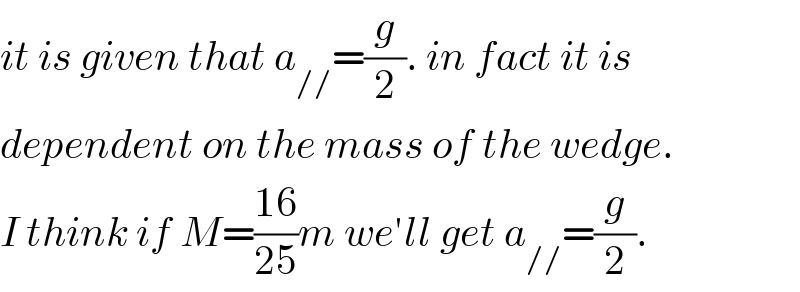
Commented by mrW1 last updated on 05/Jan/18

Commented by Tinkutara last updated on 05/Jan/18

Thank you very much Sir! I got the answer.

Commented by mrW1 last updated on 05/Jan/18

$$a_{//}=a$$$$a_{\mathrm{\perp }}=a\sin \theta$$$$let\lambda =\frac{M}{m}and\alpha =\frac{a}{g}$$$$$$$$mg\sin \theta -T={ma}_{//}=ma$$$$\Rightarrow T=mg\sin \theta -ma=mg(\sin \theta -\alpha )$$$$mg\cos \theta -N={ma}_{\mathrm{\perp }}=ma\sin \theta$$$$\Rightarrow N=mg\cos \theta -ma\sin \theta =mg(\cos \theta -\alpha \sin \theta )$$$$$$$$T-T\cos \theta +N\sin \theta =Ma$$$$T(1-\cos \theta )+N\sin \theta =Ma$$$$mg(\sin \theta -\alpha )(1-\cos \theta )+mg(\cos \theta -\alpha \sin \theta )\sin \theta =Ma$$$$(\sin \theta -\alpha )(1-\cos \theta )+(\cos \theta -\alpha \sin \theta )\sin \theta =\frac{Ma}{mg}=\lambda \alpha$$$$\sin \theta -\sin \theta \cos \theta -(1-\cos \theta )\alpha +\cos \theta \sin \theta -\alpha {\sin }^2\theta =\lambda \alpha$$$$\sin \theta -(1-\cos \theta )\alpha -\alpha {\sin }^2\theta =\lambda \alpha$$$$\sin \theta =(\lambda +1-\cos \theta +{\sin }^2\theta )\alpha$$$$\sin \theta =(\lambda +2-\cos \theta -{\cos }^2\theta )\alpha$$$$\Rightarrow \alpha =\frac{\sin \theta }{\lambda +2-\cos \theta -{\cos }^2\theta }$$$$\Rightarrow a=\frac{\sin \theta }{\frac{M}{m}+2-\cos \theta -{\cos }^2\theta }\times g$$$$with\sin \theta =\frac{3}{5}and\cos \theta =\frac{4}{5}weget$$$$a=\frac{0.6g}{\frac{M}{m}+0.56}$$$$fora=\frac{g}{2}$$$$\Rightarrow \frac{M}{m}=\frac{0.6}{0.5}-0.56=\frac{16}{25}$$

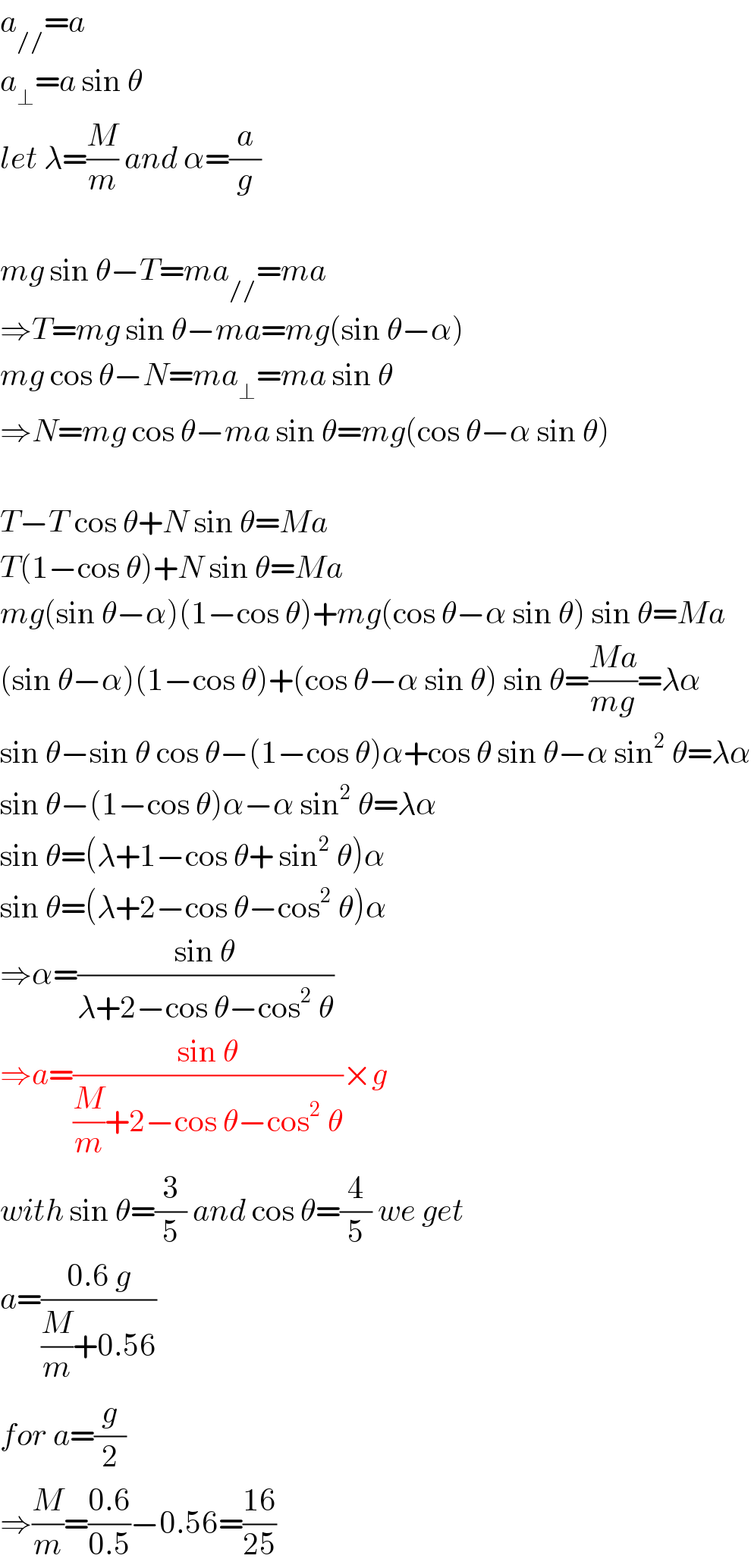
Commented by Tinkutara last updated on 05/Jan/18

I really appreciate this.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com