Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 27343 by abdo imad last updated on 05/Jan/18

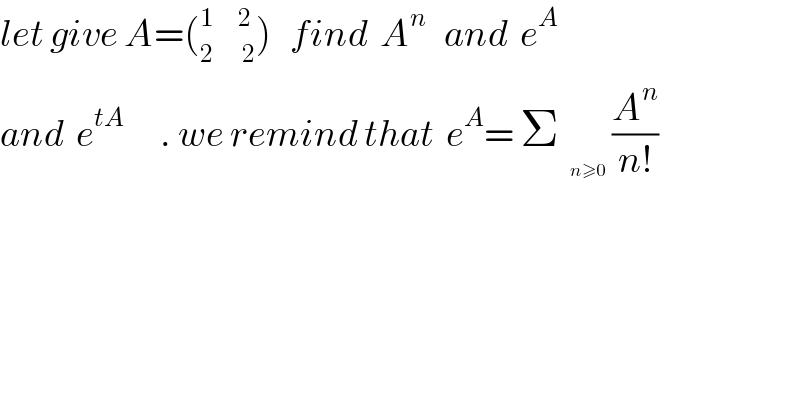
let give A=(_(2 2) ^(1 2) ) find A^n and e^A and e^(tA) . we remind that e^A = Σ_ (A^n /(n!))

$${let}\:{give}\:{A}=\left(_{\mathrm{2}\:\:\:\:\:\:\:\mathrm{2}} ^{\mathrm{1}\:\:\:\:\:\:\mathrm{2}} \right)\:\:\:{find}\:\:{A}^{{n}} \:\:\:{and}\:\:{e}^{{A}} \\ $$$${and}\:\:{e}^{{tA}} \:\:\:\:\:\:.\:{we}\:{remind}\:{that}\:\:{e}^{{A}} =\:\sum_{} \:\frac{{A}^{{n}} }{{n}!} \\ $$

Commented by Rasheed.Sindhi last updated on 05/Jan/18

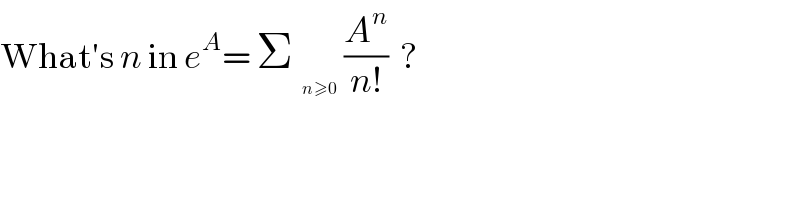
What′s n in e^A = Σ_ (A^n /(n!)) ?

$$\mathrm{What}'\mathrm{s}\:{n}\:\mathrm{in}\:{e}^{{A}} =\:\sum_{} \:\frac{{A}^{{n}} }{{n}!}\:\:? \\ $$

Commented by abdo imad last updated on 05/Jan/18

n integer.

$${n}\:{integer}. \\ $$

Commented by Rasheed.Sindhi last updated on 06/Jan/18

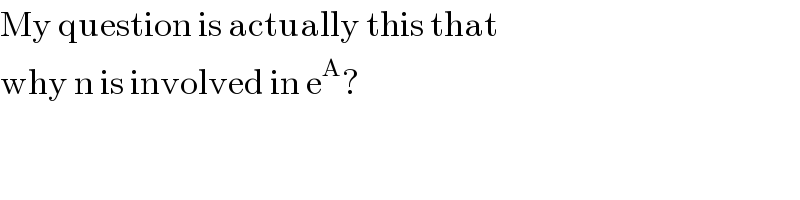
My question is actually this that why n is involved in e^A ?

$$\mathrm{My}\:\mathrm{question}\:\mathrm{is}\:\mathrm{actually}\:\mathrm{this}\:\mathrm{that} \\ $$$$\mathrm{why}\:\mathrm{n}\:\mathrm{is}\:\mathrm{involved}\:\mathrm{in}\:\mathrm{e}^{\mathrm{A}} ? \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jan/18

thanks sir. I misunderstood.

$${thanks}\:{sir}.\:{I}\:{misunderstood}. \\ $$

Commented by prakash jain last updated on 06/Jan/18

e^x =Σ_(i=0) ^∞ (x^i /(i!))

$${e}^{{x}} =\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{i}} }{{i}!} \\ $$

Commented by Rasheed.Sindhi last updated on 06/Jan/18

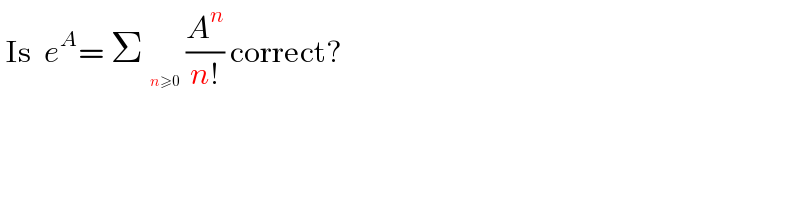
Is e^A = Σ_ (A^n /(n!)) correct?

$$\:\mathrm{Is}\:\:{e}^{{A}} =\:\sum_{} \:\frac{{A}^{{n}} }{{n}!}\:\mathrm{correct}? \\ $$

Commented by abdo imad last updated on 06/Jan/18

e^A is also a matrise defined by e^A = Σ_(n≥0) (A^n /(n!)) like e^x = Σ (x^n /(n!))

$${e}^{{A}} \:{is}\:{also}\:{a}\:{matrise}\:{defined}\:{by}\: \\ $$$${e}^{{A}} =\:\sum_{{n}\geqslant\mathrm{0}} \:\:\frac{{A}^{{n}} }{{n}!}\:\:{like}\:\:{e}^{{x}} =\:\Sigma\:\frac{{x}^{{n}} }{{n}!}\: \\ $$

Answered by prakash jain last updated on 07/Jan/18

A^n = ((a_(n−1) ,b_(n−1) ),(c_(n−1) ,d_(n−1) ) ) ∙ ((1,2),(2,2) ) a_n =a_(n−1) +2b_(n−1) b_n =2a_(n−1) +2b_(n−1) c_n =2c_(n−1) +2d_(n−1) c_n =2c_(n−1) +2d_(n−1) b_(n−1) =((a_n −a_(n−1) )/2) b_n =2a_(n−1) +2b_(n−1) =a_n +a_(n−1) a_n =a_(n−1) +2b_(n−1) =a_(n−1) +2a_(n−1) +2a_(n−2) a_n −3a_(n−1) −2a_(n−2) =0 x^2 −3x−2=0⇒x=((3±(√(17)))/2) a_n =c_1 (((3+(√(17)))/2))^n +c_2 (((3−(√(17)))/2))^n a_1 =1⇒c_1 (3+(√(17)))+c_2 (3−(√(17)))=1 a_2 =5⇒c_1 (3+(√(17)))^2 +c_2 (3−(√(17)))^2 =20 c_1 =((20−(3−(√(17))))/((3+(√(17)))^2 −(3+(√(17)))(3−(√(17))))) =((17+(√(17)))/(9+17+6(√(17))−9+17))=((17+(√(17)))/(34+6(√(17)))) =((1+(√(17)))/(2((√(17))+3))) c_2 =((20−(3+(√(17))))/((3−(√(17)))^2 −(3+(√(17)))(3−(√(17)))))=((17−(√(17)))/(34−6(√(17)))) c_2 =((1−(√(17)))/(2(3−(√(17))))) Similarly we can find b_n ,c_n and d_n .

$${A}^{{n}} =\begin{pmatrix}{{a}_{{n}−\mathrm{1}} }&{{b}_{{n}−\mathrm{1}} }\\{{c}_{{n}−\mathrm{1}} }&{{d}_{{n}−\mathrm{1}} }\end{pmatrix}\:\centerdot\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}\\{\mathrm{2}}&{\mathrm{2}}\end{pmatrix} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}{b}_{{n}−\mathrm{1}} \\ $$$${b}_{{n}} =\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{2}{b}_{{n}−\mathrm{1}} \\ $$$${c}_{{n}} =\mathrm{2}{c}_{{n}−\mathrm{1}} +\mathrm{2}{d}_{{n}−\mathrm{1}} \\ $$$${c}_{{n}} =\mathrm{2}{c}_{{n}−\mathrm{1}} +\mathrm{2}{d}_{{n}−\mathrm{1}} \\ $$$${b}_{{n}−\mathrm{1}} =\frac{{a}_{{n}} −{a}_{{n}−\mathrm{1}} }{\mathrm{2}} \\ $$$${b}_{{n}} =\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{2}{b}_{{n}−\mathrm{1}} ={a}_{{n}} +{a}_{{n}−\mathrm{1}} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}{b}_{{n}−\mathrm{1}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{2}{a}_{{n}−\mathrm{2}} \\ $$$${a}_{{n}} −\mathrm{3}{a}_{{n}−\mathrm{1}} −\mathrm{2}{a}_{{n}−\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{2}=\mathrm{0}\Rightarrow{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$${a}_{{n}} ={c}_{\mathrm{1}} \left(\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} +{c}_{\mathrm{2}} \left(\frac{\mathrm{3}−\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} \\ $$$${a}_{\mathrm{1}} =\mathrm{1}\Rightarrow{c}_{\mathrm{1}} \left(\mathrm{3}+\sqrt{\mathrm{17}}\right)+{c}_{\mathrm{2}} \left(\mathrm{3}−\sqrt{\mathrm{17}}\right)=\mathrm{1} \\ $$$${a}_{\mathrm{2}} =\mathrm{5}\Rightarrow{c}_{\mathrm{1}} \left(\mathrm{3}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} +{c}_{\mathrm{2}} \left(\mathrm{3}−\sqrt{\mathrm{17}}\right)^{\mathrm{2}} =\mathrm{20} \\ $$$${c}_{\mathrm{1}} =\frac{\mathrm{20}−\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)}{\left(\mathrm{3}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{3}+\sqrt{\mathrm{17}}\right)\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)} \\ $$$$=\frac{\mathrm{17}+\sqrt{\mathrm{17}}}{\mathrm{9}+\mathrm{17}+\mathrm{6}\sqrt{\mathrm{17}}−\mathrm{9}+\mathrm{17}}=\frac{\mathrm{17}+\sqrt{\mathrm{17}}}{\mathrm{34}+\mathrm{6}\sqrt{\mathrm{17}}} \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}\left(\sqrt{\mathrm{17}}+\mathrm{3}\right)} \\ $$$${c}_{\mathrm{2}} =\frac{\mathrm{20}−\left(\mathrm{3}+\sqrt{\mathrm{17}}\right)}{\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{3}+\sqrt{\mathrm{17}}\right)\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)}=\frac{\mathrm{17}−\sqrt{\mathrm{17}}}{\mathrm{34}−\mathrm{6}\sqrt{\mathrm{17}}} \\ $$$${c}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)} \\ $$$$\mathrm{Similarly}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:{b}_{{n}} ,{c}_{{n}} \:\mathrm{and}\:{d}_{{n}} . \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com