
Question and Answers Forum
Question Number 27384 by abdo imad last updated on 05/Jan/18
![let give p(x)= (((1+ix)/(1−ix)))^n − ((1+itanα )/(1−itanα)) factorize p(x) inside C[x].](Q27384.png)
Commented by abdo imad last updated on 07/Jan/18
![roots of p(x) p(x)=0⇔ (((1+ix)/(1−ix)) )^n = ((1+itanα)/(1−itanα))=((cosα +isinα)/(cosα −isinα)) =e^(i(2α)) let put ((1+ix)/(1−ix))= t so p(x)=0⇔ t^n = e^(i(2α)) wich have for solutions t_k =e^(i2(α+kπ)(1/n)) and k∈[[0,n−1]] but ((1+ix)/(1−ix))=t_k ⇔ 1+ix=(1−ix)t_k ⇔ ix(1+t_k )=t_k −1 ix =((t_k −1)/(1+t_k )) ⇔x =−i((t_k −1)/(1+tk)) =i ((1−t_k )/(1+t_k )) so the complex wich verify p(x)=0 are x_k = i ((1−t_k )/(1+t_k )) and k∈[[0,n−1]] but x_k = i ((1−e^(i2((α+kπ)/n)) )/(1+ e^(i2((α+kπ)/n)) )) =i((1−cos(2((α+kπ)/n)) −i sin(2((α+kπ)/n)))/(1+cos(2((α+kπ)/n))+isin(2((α+kπ)/n)))) x_(k ) =tan(((α+kπ)/n)) with k from[[0,n−1]] so p(x)= λ Π_(k=0) ^(n−1) (x−tan(((α+kπ)/n))) .](Q27505.png)
Answered by sma3l2996 last updated on 06/Jan/18
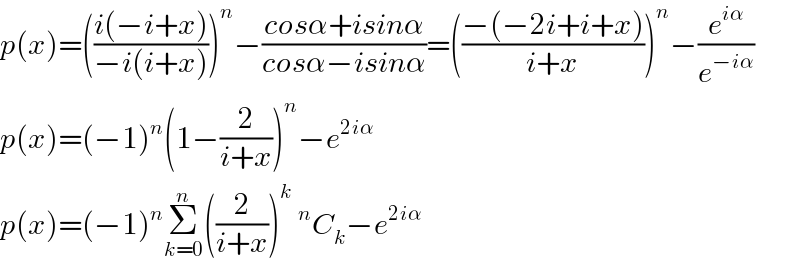
| ||
Question and Answers Forum | ||
Question Number 27384 by abdo imad last updated on 05/Jan/18 | ||
![let give p(x)= (((1+ix)/(1−ix)))^n − ((1+itanα )/(1−itanα)) factorize p(x) inside C[x].](Q27384.png) | ||
Commented by abdo imad last updated on 07/Jan/18 | ||
![roots of p(x) p(x)=0⇔ (((1+ix)/(1−ix)) )^n = ((1+itanα)/(1−itanα))=((cosα +isinα)/(cosα −isinα)) =e^(i(2α)) let put ((1+ix)/(1−ix))= t so p(x)=0⇔ t^n = e^(i(2α)) wich have for solutions t_k =e^(i2(α+kπ)(1/n)) and k∈[[0,n−1]] but ((1+ix)/(1−ix))=t_k ⇔ 1+ix=(1−ix)t_k ⇔ ix(1+t_k )=t_k −1 ix =((t_k −1)/(1+t_k )) ⇔x =−i((t_k −1)/(1+tk)) =i ((1−t_k )/(1+t_k )) so the complex wich verify p(x)=0 are x_k = i ((1−t_k )/(1+t_k )) and k∈[[0,n−1]] but x_k = i ((1−e^(i2((α+kπ)/n)) )/(1+ e^(i2((α+kπ)/n)) )) =i((1−cos(2((α+kπ)/n)) −i sin(2((α+kπ)/n)))/(1+cos(2((α+kπ)/n))+isin(2((α+kπ)/n)))) x_(k ) =tan(((α+kπ)/n)) with k from[[0,n−1]] so p(x)= λ Π_(k=0) ^(n−1) (x−tan(((α+kπ)/n))) .](Q27505.png) | ||
Answered by sma3l2996 last updated on 06/Jan/18 | ||
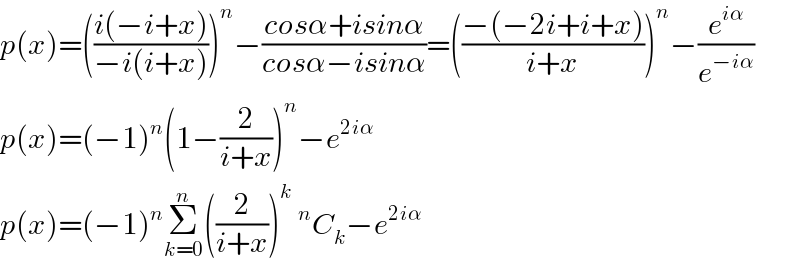 | ||
| ||