
Question and Answers Forum
Question Number 27500 by abdo imad last updated on 07/Jan/18
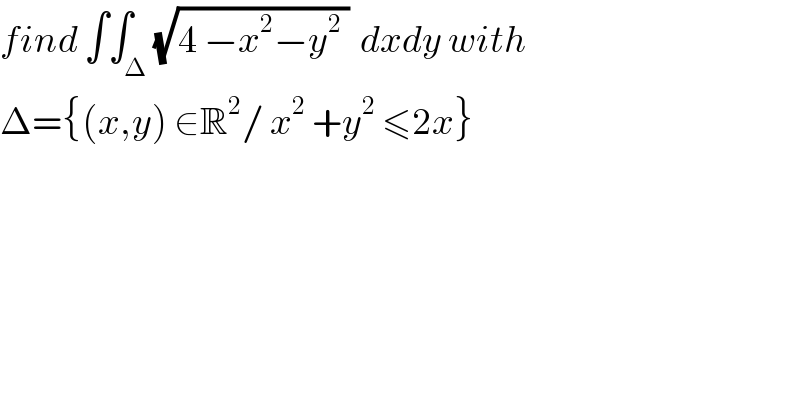
Commented by abdo imad last updated on 10/Jan/18
![let use the changement x=rcosθ and y=rsinθ x^2 +y^2 ≤2x ⇔ r^2 ≤ 2r cosθ ⇔ 0<r≤ 2cosθ I= ∫∫_(−_ (π/2)<θ<(π/2) and 0<r≤2cosθ) (√( 4−r^2 )) rdrdθ I =∫_(−(π/2)) ^(π/2) ( ∫_0 ^(2cosθ) r(√( 4−r^2 )) dr)dθ but ∫_0 ^(2cosθ) r(√(4−r^2 )) dr = [−(1/3)(4−r^2 )^(3/2) ]_0 ^(2cosθ) = −(1/3)((4−4cos^2 θ)^(3/2) −4^(3/2) =−(1/3)(4^(3/2) (sin^2 )^(3/2) −8)= −(1/3)(8 sin^3 θ −8 ) I= −(8/3) ∫_(−(π/2)) ^(π/2) (sin^3 θ −1)dθ = ((8π)/3) −(8/3) ∫_(−(π/2)) ^(π/2) sin^3 θdθ we find the value of I by linearisation of sin^3 θ....](Q27575.png)
Commented by abdo imad last updated on 10/Jan/18
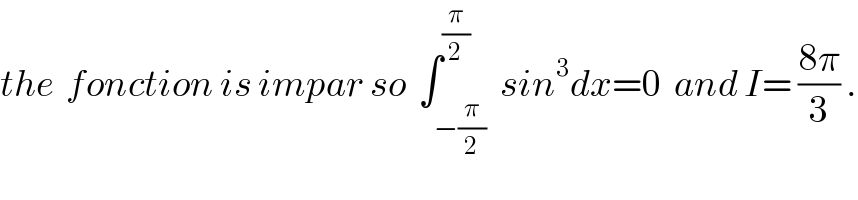
| ||
Question and Answers Forum | ||
Question Number 27500 by abdo imad last updated on 07/Jan/18 | ||
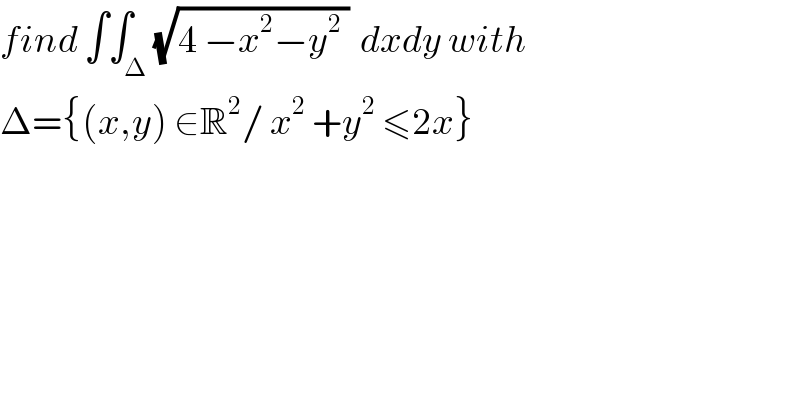 | ||
Commented by abdo imad last updated on 10/Jan/18 | ||
![let use the changement x=rcosθ and y=rsinθ x^2 +y^2 ≤2x ⇔ r^2 ≤ 2r cosθ ⇔ 0<r≤ 2cosθ I= ∫∫_(−_ (π/2)<θ<(π/2) and 0<r≤2cosθ) (√( 4−r^2 )) rdrdθ I =∫_(−(π/2)) ^(π/2) ( ∫_0 ^(2cosθ) r(√( 4−r^2 )) dr)dθ but ∫_0 ^(2cosθ) r(√(4−r^2 )) dr = [−(1/3)(4−r^2 )^(3/2) ]_0 ^(2cosθ) = −(1/3)((4−4cos^2 θ)^(3/2) −4^(3/2) =−(1/3)(4^(3/2) (sin^2 )^(3/2) −8)= −(1/3)(8 sin^3 θ −8 ) I= −(8/3) ∫_(−(π/2)) ^(π/2) (sin^3 θ −1)dθ = ((8π)/3) −(8/3) ∫_(−(π/2)) ^(π/2) sin^3 θdθ we find the value of I by linearisation of sin^3 θ....](Q27575.png) | ||
Commented by abdo imad last updated on 10/Jan/18 | ||
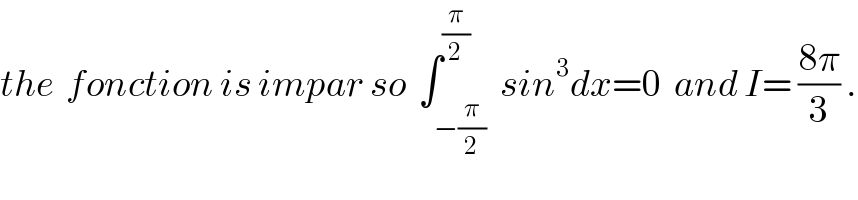 | ||