
Question and Answers Forum
Question Number 27595 by abdo imad last updated on 10/Jan/18
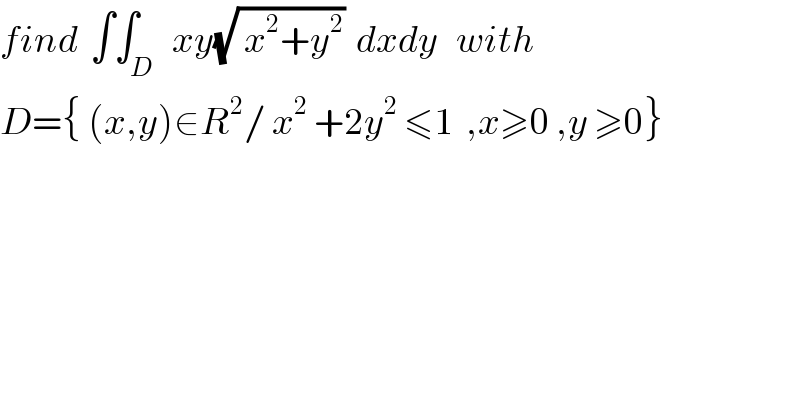
Commented by abdo imad last updated on 15/Jan/18
![we use the polar coordinate let use the ch.x=rcosθ and y= (1/(√2)) sinθ due to the diffeomorphisme we must have 0≤θ≤ (π/2) and 0≤r≤1 I=∫∫_D xy(√(x^2 +2y^2 )) dxdy= ∫∫_w Φof/j_Φ /dr dθ (r,θ)−(f_1 (r,θ) ,f_2 (r,θ))=(x y ) =(rcosθ ,(r/(√2)) sinθ) M_j = (_((1/(√2))sinθ) ^(cosθ) _((r/(√2))cosθ)^(−rsinθ) ) I=∫∫_(0≤r≤1 and 0≤θ≤(π/2)) rcosθ.(r/(√2)) sinθ r .(r/(√2)) drdθ I= (1/2)∫_0^ ^1 r^4 ∫_0 ^(π/(2 )) cosθ sinθ dθ = (1/4) [(1/5) r^5 ]_0 ^1 ∫_0 ^(π/2) sin(2θ)dθ = (1/(40)) [−cos(2θ)]_0 ^(π/2) = (1/(20)) .](Q27877.png)
| ||
Question and Answers Forum | ||
Question Number 27595 by abdo imad last updated on 10/Jan/18 | ||
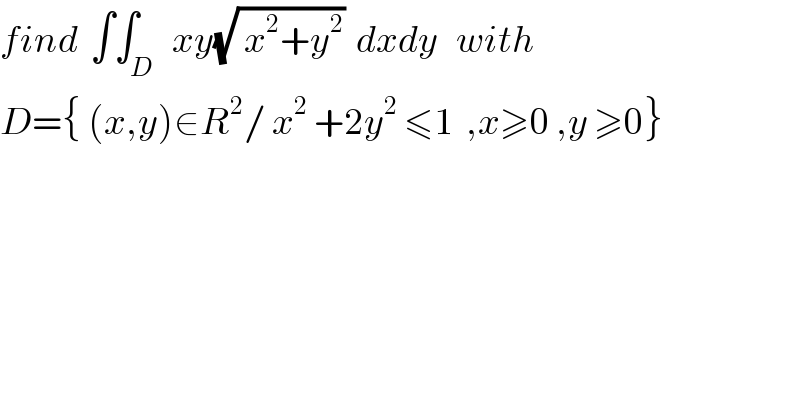 | ||
Commented by abdo imad last updated on 15/Jan/18 | ||
![we use the polar coordinate let use the ch.x=rcosθ and y= (1/(√2)) sinθ due to the diffeomorphisme we must have 0≤θ≤ (π/2) and 0≤r≤1 I=∫∫_D xy(√(x^2 +2y^2 )) dxdy= ∫∫_w Φof/j_Φ /dr dθ (r,θ)−(f_1 (r,θ) ,f_2 (r,θ))=(x y ) =(rcosθ ,(r/(√2)) sinθ) M_j = (_((1/(√2))sinθ) ^(cosθ) _((r/(√2))cosθ)^(−rsinθ) ) I=∫∫_(0≤r≤1 and 0≤θ≤(π/2)) rcosθ.(r/(√2)) sinθ r .(r/(√2)) drdθ I= (1/2)∫_0^ ^1 r^4 ∫_0 ^(π/(2 )) cosθ sinθ dθ = (1/4) [(1/5) r^5 ]_0 ^1 ∫_0 ^(π/2) sin(2θ)dθ = (1/(40)) [−cos(2θ)]_0 ^(π/2) = (1/(20)) .](Q27877.png) | ||