
Question and Answers Forum
Question Number 27598 by abdo imad last updated on 10/Jan/18
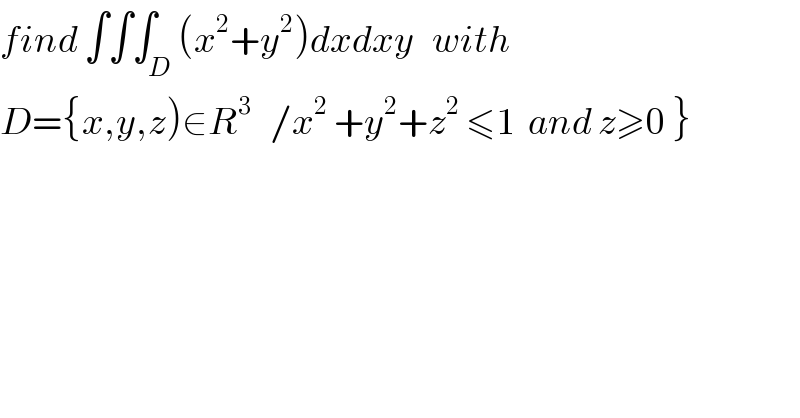
Commented by abdo imad last updated on 21/Jan/18
![we have z^2 ≤ 1−(x^2 +y^2 ) ≤1 and z≥0 ⇒ 0≤z≤1 so I= ∫∫∫ (x^2 +y^2 +z^2 )dxdydz = ∫_0 ^1 (∫∫_W (x^2 +y^2 )dxdy)dz with W ={ (x,y)∈R^2 / x^2 +y^2 ≤1−z^2 and z≥0} let define a diffeomorphisme on W we use the polar coordinate x=r cosθ and y =rsinθ we must have 0<r ≤(√(1−z^2 )) and 0≤θ≤2π ∫∫_W ( x^2 +y^2 )dxdy= ∫∫_(0<r≤(√(1−z^2 )) and 0≤θ≤2π) r^2 rdrdθ = 2π ∫_0 ^(√(1−z^2 )) r^3 dr = (π/2) [ r^4 ]_0 ^(√(1−z^2 )) = (π/2)(1−z^2 )^2 = (π/2)( z^4 −2z^2 +1) and I= (π/2) ∫_0 ^1 (z^4 −2z^2 +1)dz =(π/2) [ (z^5 /5) −(2/3) z^3 +z]_0 ^1 = (π/2) ( (1/5) −(2/3) +1) = (π/2)( (1/5) +(1/3)) = ((8π)/(30)) = ((4π)/(15)) .](Q28136.png)
| ||
Question and Answers Forum | ||
Question Number 27598 by abdo imad last updated on 10/Jan/18 | ||
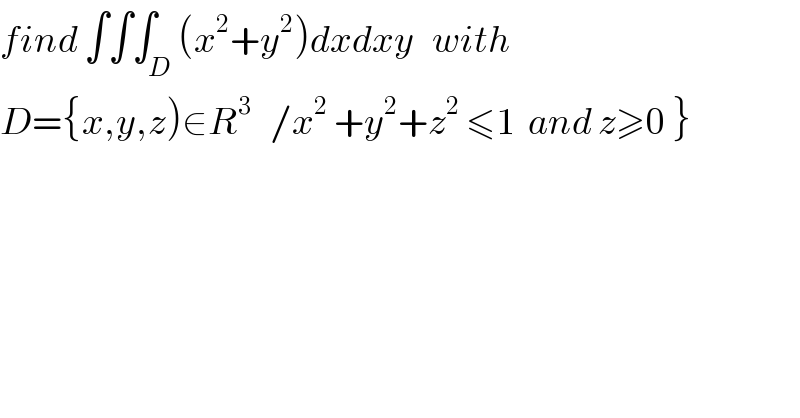 | ||
Commented by abdo imad last updated on 21/Jan/18 | ||
![we have z^2 ≤ 1−(x^2 +y^2 ) ≤1 and z≥0 ⇒ 0≤z≤1 so I= ∫∫∫ (x^2 +y^2 +z^2 )dxdydz = ∫_0 ^1 (∫∫_W (x^2 +y^2 )dxdy)dz with W ={ (x,y)∈R^2 / x^2 +y^2 ≤1−z^2 and z≥0} let define a diffeomorphisme on W we use the polar coordinate x=r cosθ and y =rsinθ we must have 0<r ≤(√(1−z^2 )) and 0≤θ≤2π ∫∫_W ( x^2 +y^2 )dxdy= ∫∫_(0<r≤(√(1−z^2 )) and 0≤θ≤2π) r^2 rdrdθ = 2π ∫_0 ^(√(1−z^2 )) r^3 dr = (π/2) [ r^4 ]_0 ^(√(1−z^2 )) = (π/2)(1−z^2 )^2 = (π/2)( z^4 −2z^2 +1) and I= (π/2) ∫_0 ^1 (z^4 −2z^2 +1)dz =(π/2) [ (z^5 /5) −(2/3) z^3 +z]_0 ^1 = (π/2) ( (1/5) −(2/3) +1) = (π/2)( (1/5) +(1/3)) = ((8π)/(30)) = ((4π)/(15)) .](Q28136.png) | ||