
Question and Answers Forum
Question Number 27600 by abdo imad last updated on 10/Jan/18
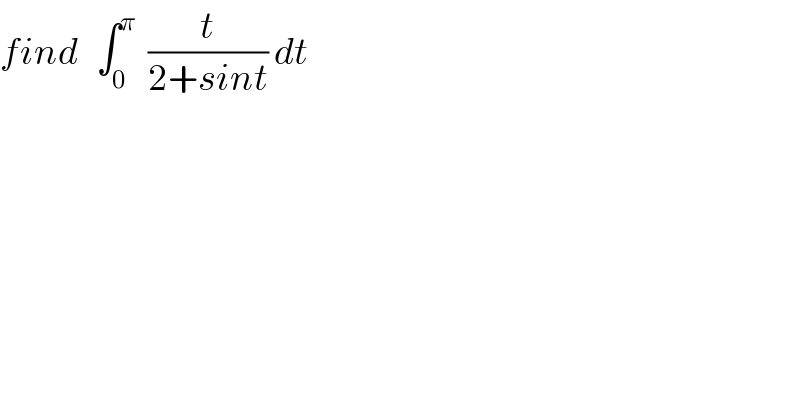
Commented by abdo imad last updated on 11/Jan/18
![let put I=∫_0 ^π (t/(2+sint))dt and the ch. tan((t/2))=x⇔ t=2arctanx I= ∫_0 ^∞ ((2arctanx)/(2+((2x)/(1+x^2 )))) ((2dx)/(1+x^2 ))= 2 ∫_0 ^∞ ((arctanx)/(1+x^2 +2x))dx =2∫_0 ^∞ ((arctanx)/((x+1)^2 ))dx then the integration per parts give ∫_0 ^∞ ((arctanx)/((x+1)^2 ))dx= [−(1/(x+1)) arctanx]_0 ^∝ − ∫_0 ^∞ −(1/(x+1)) (dx/(1+x^2 )) = ∫_0 ^∞ (dx/((x+1)(1+x^2 ))) let decompose rational fraction F(x)= (1/((x+1)(1+x^2 )))⇒F(x)= (a/(x+1)) + ((bx+c)/(1+x^2 )) a= lim_(x−>−1^ ) (x+1)F(x)= (1/2) lim_(x−>∝) xF(x)=0=a+b⇒b=−(1/2) so F(x)= (1/(2(x+1))) + ((((−x)/2)+c)/(1+x^2 )) ,F(0)=1= (1/2)+c⇒c=(1/2) F(x)= (1/(2(x+1))) −(1/2) ((x−1)/(1+x^2 )) I= ∫_0 ^∞ (dx/(x+1)) −∫_0 ^∞ ((x−1)/(1+x^2 ))dx = ∫_0 ^∞ (dx/(x+1)) −(1/2) ∫_0 ^∞ ((2x−2)/(1+x^2 ))dx I= ∫_0 ^∞ ( (1/(x+1)) −(1/2)((2x)/(1+x^2 )))dx + ∫_0 ^∞ (dx/(1+x^2 )) I=[ln/x+1/−(1/2)ln/1+x^2 /]_0 ^∝ + (π/2) I=[ln/((x+1)/(√(1+x^2 )))/ ]_0 ^∝ +(π/2)=0+(π/2) ∫_0 ^π (t/(2+sint))dt = (π/2) .](Q27644.png)
| ||
Question and Answers Forum | ||
Question Number 27600 by abdo imad last updated on 10/Jan/18 | ||
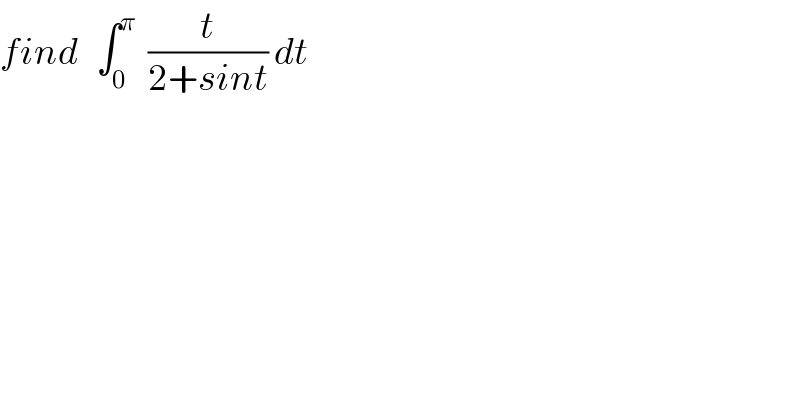 | ||
Commented by abdo imad last updated on 11/Jan/18 | ||
![let put I=∫_0 ^π (t/(2+sint))dt and the ch. tan((t/2))=x⇔ t=2arctanx I= ∫_0 ^∞ ((2arctanx)/(2+((2x)/(1+x^2 )))) ((2dx)/(1+x^2 ))= 2 ∫_0 ^∞ ((arctanx)/(1+x^2 +2x))dx =2∫_0 ^∞ ((arctanx)/((x+1)^2 ))dx then the integration per parts give ∫_0 ^∞ ((arctanx)/((x+1)^2 ))dx= [−(1/(x+1)) arctanx]_0 ^∝ − ∫_0 ^∞ −(1/(x+1)) (dx/(1+x^2 )) = ∫_0 ^∞ (dx/((x+1)(1+x^2 ))) let decompose rational fraction F(x)= (1/((x+1)(1+x^2 )))⇒F(x)= (a/(x+1)) + ((bx+c)/(1+x^2 )) a= lim_(x−>−1^ ) (x+1)F(x)= (1/2) lim_(x−>∝) xF(x)=0=a+b⇒b=−(1/2) so F(x)= (1/(2(x+1))) + ((((−x)/2)+c)/(1+x^2 )) ,F(0)=1= (1/2)+c⇒c=(1/2) F(x)= (1/(2(x+1))) −(1/2) ((x−1)/(1+x^2 )) I= ∫_0 ^∞ (dx/(x+1)) −∫_0 ^∞ ((x−1)/(1+x^2 ))dx = ∫_0 ^∞ (dx/(x+1)) −(1/2) ∫_0 ^∞ ((2x−2)/(1+x^2 ))dx I= ∫_0 ^∞ ( (1/(x+1)) −(1/2)((2x)/(1+x^2 )))dx + ∫_0 ^∞ (dx/(1+x^2 )) I=[ln/x+1/−(1/2)ln/1+x^2 /]_0 ^∝ + (π/2) I=[ln/((x+1)/(√(1+x^2 )))/ ]_0 ^∝ +(π/2)=0+(π/2) ∫_0 ^π (t/(2+sint))dt = (π/2) .](Q27644.png) | ||