Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 33619 by NECx last updated on 20/Apr/18

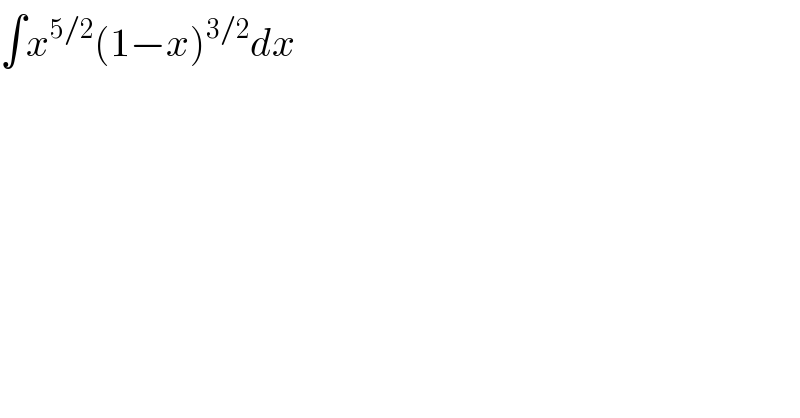
∫x^(5/2) (1−x)^(3/2) dx

$$\int{x}^{\mathrm{5}/\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} {dx} \\ $$

Commented by abdo imad last updated on 20/Apr/18

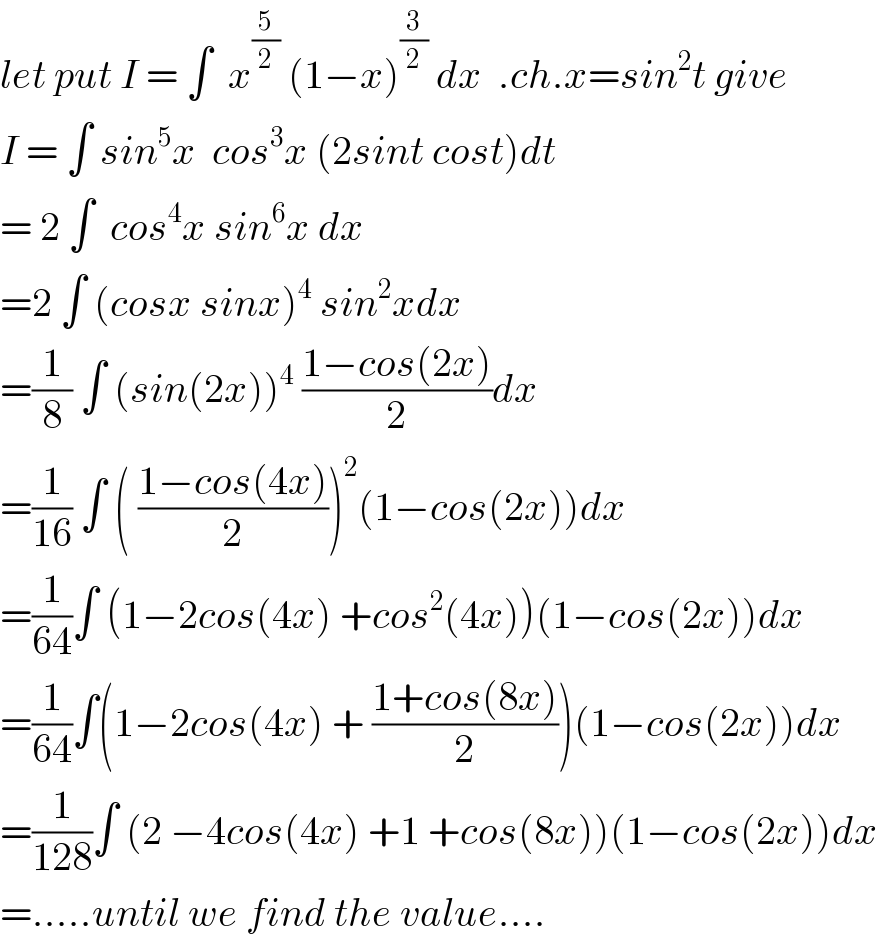
let put I = ∫ x^(5/2) (1−x)^(3/2) dx .ch.x=sin^2 t give I = ∫ sin^5 x cos^3 x (2sint cost)dt = 2 ∫ cos^4 x sin^6 x dx =2 ∫ (cosx sinx)^4 sin^2 xdx =(1/8) ∫ (sin(2x))^4 ((1−cos(2x))/2)dx =(1/(16)) ∫ ( ((1−cos(4x))/2))^2 (1−cos(2x))dx =(1/(64))∫ (1−2cos(4x) +cos^2 (4x))(1−cos(2x))dx =(1/(64))∫(1−2cos(4x) + ((1+cos(8x))/2))(1−cos(2x))dx =(1/(128))∫ (2 −4cos(4x) +1 +cos(8x))(1−cos(2x))dx =.....until we find the value....

$${let}\:{put}\:{I}\:=\:\int\:\:{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:{dx}\:\:.{ch}.{x}={sin}^{\mathrm{2}} {t}\:{give} \\ $$$${I}\:=\:\int\:{sin}^{\mathrm{5}} {x}\:\:{cos}^{\mathrm{3}} {x}\:\left(\mathrm{2}{sint}\:{cost}\right){dt} \\ $$$$=\:\mathrm{2}\:\int\:\:{cos}^{\mathrm{4}} {x}\:{sin}^{\mathrm{6}} {x}\:{dx} \\ $$$$=\mathrm{2}\:\int\:\left({cosx}\:{sinx}\right)^{\mathrm{4}} \:{sin}^{\mathrm{2}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int\:\left({sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{4}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\:\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{4}{x}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{4}{x}\right)\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{4}{x}\right)\:+\:\frac{\mathrm{1}+{cos}\left(\mathrm{8}{x}\right)}{\mathrm{2}}\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{128}}\int\:\left(\mathrm{2}\:−\mathrm{4}{cos}\left(\mathrm{4}{x}\right)\:+\mathrm{1}\:+{cos}\left(\mathrm{8}{x}\right)\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=.....{until}\:{we}\:{find}\:{the}\:{value}.... \\ $$

Commented by abdo imad last updated on 20/Apr/18

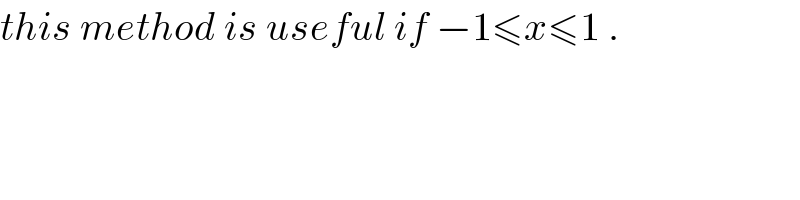
this method is useful if −1≤x≤1 .

$${this}\:{method}\:{is}\:{useful}\:{if}\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1}\:. \\ $$

Commented by NECx last updated on 21/Apr/18

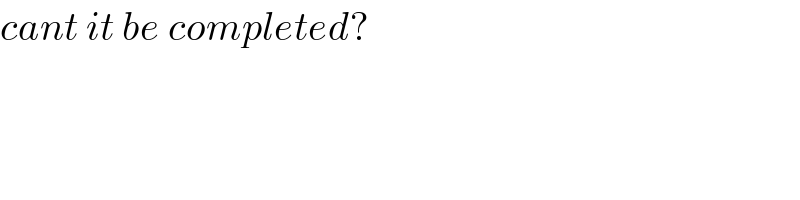
cant it be completed?

$${cant}\:{it}\:{be}\:{completed}? \\ $$$$ \\ $$

Answered by MJS last updated on 21/Apr/18

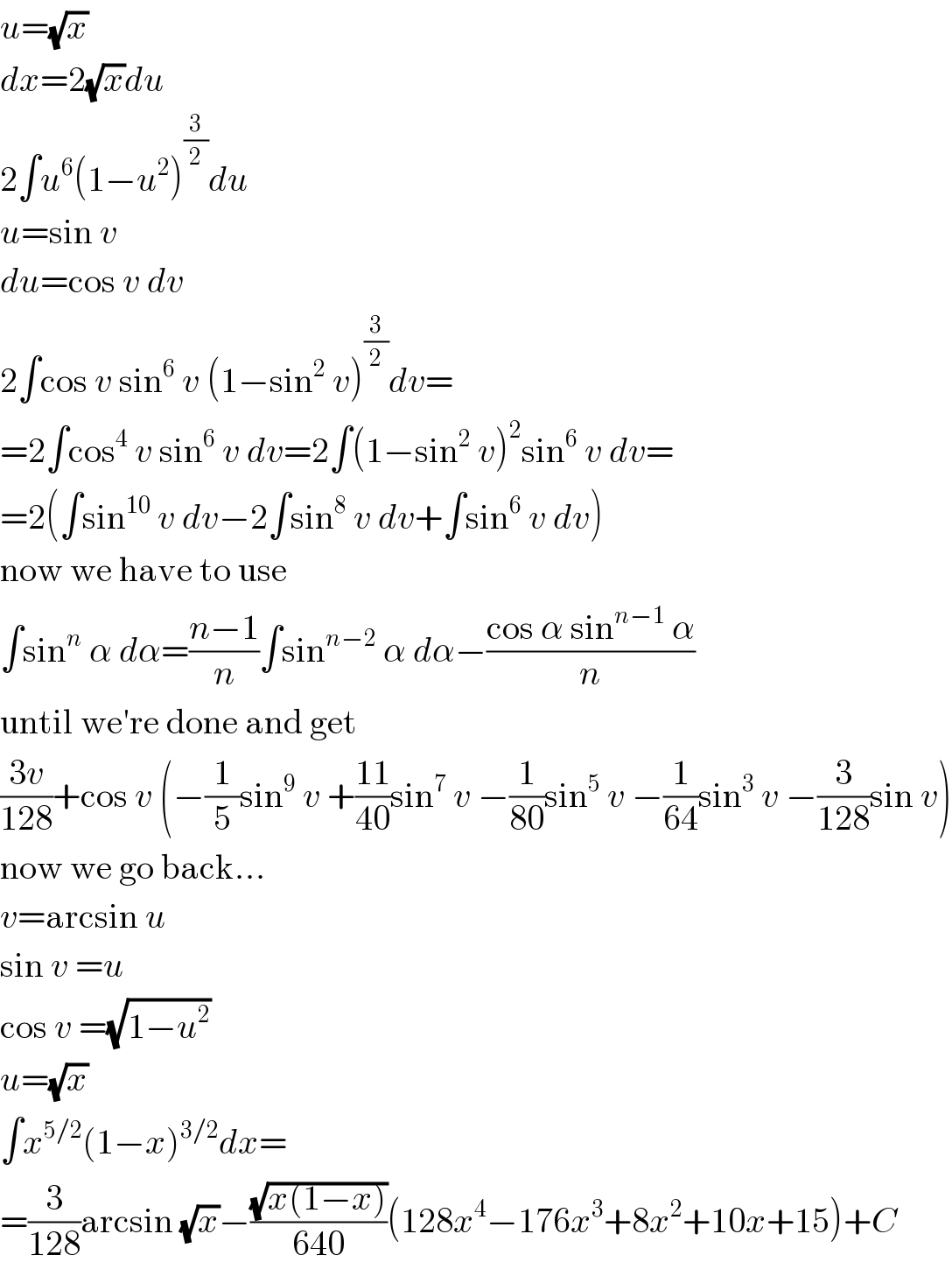
u=(√x) dx=2(√x)du 2∫u^6 (1−u^2 )^(3/2) du u=sin v du=cos v dv 2∫cos v sin^6 v (1−sin^2 v)^(3/2) dv= =2∫cos^4 v sin^6 v dv=2∫(1−sin^2 v)^2 sin^6 v dv= =2(∫sin^(10) v dv−2∫sin^8 v dv+∫sin^6 v dv) now we have to use ∫sin^n α dα=((n−1)/n)∫sin^(n−2) α dα−((cos α sin^(n−1) α)/n) until we′re done and get ((3v)/(128))+cos v (−(1/5)sin^9 v +((11)/(40))sin^7 v −(1/(80))sin^5 v −(1/(64))sin^3 v −(3/(128))sin v) now we go back... v=arcsin u sin v =u cos v =(√(1−u^2 )) u=(√x) ∫x^(5/2) (1−x)^(3/2) dx= =(3/(128))arcsin (√x)−((√(x(1−x)))/(640))(128x^4 −176x^3 +8x^2 +10x+15)+C

$${u}=\sqrt{{x}} \\ $$$${dx}=\mathrm{2}\sqrt{{x}}{du} \\ $$$$\mathrm{2}\int{u}^{\mathrm{6}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} {du} \\ $$$${u}=\mathrm{sin}\:{v} \\ $$$${du}=\mathrm{cos}\:{v}\:{dv} \\ $$$$\mathrm{2}\int\mathrm{cos}\:{v}\:\mathrm{sin}^{\mathrm{6}} \:{v}\:\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{v}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dv}= \\ $$$$=\mathrm{2}\int\mathrm{cos}^{\mathrm{4}} \:{v}\:\mathrm{sin}^{\mathrm{6}} \:{v}\:{dv}=\mathrm{2}\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{v}\right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{6}} \:{v}\:{dv}= \\ $$$$=\mathrm{2}\left(\int\mathrm{sin}^{\mathrm{10}} \:{v}\:{dv}−\mathrm{2}\int\mathrm{sin}^{\mathrm{8}} \:{v}\:{dv}+\int\mathrm{sin}^{\mathrm{6}} \:{v}\:{dv}\right) \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{use} \\ $$$$\int\mathrm{sin}^{{n}} \:\alpha\:{d}\alpha=\frac{{n}−\mathrm{1}}{{n}}\int\mathrm{sin}^{{n}−\mathrm{2}} \:\alpha\:{d}\alpha−\frac{\mathrm{cos}\:\alpha\:\mathrm{sin}^{{n}−\mathrm{1}} \:\alpha}{{n}} \\ $$$$\mathrm{until}\:\mathrm{we}'\mathrm{re}\:\mathrm{done}\:\mathrm{and}\:\mathrm{get} \\ $$$$\frac{\mathrm{3}{v}}{\mathrm{128}}+\mathrm{cos}\:{v}\:\left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}^{\mathrm{9}} \:{v}\:+\frac{\mathrm{11}}{\mathrm{40}}\mathrm{sin}^{\mathrm{7}} \:{v}\:−\frac{\mathrm{1}}{\mathrm{80}}\mathrm{sin}^{\mathrm{5}} \:{v}\:−\frac{\mathrm{1}}{\mathrm{64}}\mathrm{sin}^{\mathrm{3}} \:{v}\:−\frac{\mathrm{3}}{\mathrm{128}}\mathrm{sin}\:{v}\right) \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{go}\:\mathrm{back}... \\ $$$${v}=\mathrm{arcsin}\:{u} \\ $$$$\mathrm{sin}\:{v}\:={u} \\ $$$$\mathrm{cos}\:{v}\:=\sqrt{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$${u}=\sqrt{{x}} \\ $$$$\int{x}^{\mathrm{5}/\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} {dx}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{128}}\mathrm{arcsin}\:\sqrt{{x}}−\frac{\sqrt{{x}\left(\mathrm{1}−{x}\right)}}{\mathrm{640}}\left(\mathrm{128}{x}^{\mathrm{4}} −\mathrm{176}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{15}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com