
Question and Answers Forum
Question Number 27690 by abdo imad last updated on 12/Jan/18
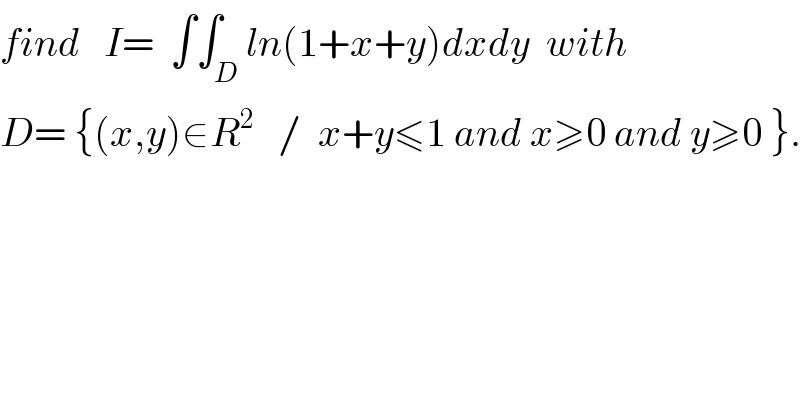
Commented by abdo imad last updated on 14/Jan/18
![0≤x≤1−y and 0≤y≤1 so I = ∫_0 ^1 ( ∫_0 ^(1−y) ln(1+x+y)dx)dy but the ch. 1+x+y =t give ∫_0 ^(1−y) ln(1+x +y)dx= ∫_(1+y) ^2 lnt dt = [tlnt −t]_(1+y) ^2 = 2ln2 −2 −(1+y)ln(1+y) +1+y =2ln2 −1 +y −(1+y)ln(1+y) I= ∫_0 ^1 (2ln2−1)dy +∫_0 ^1 ydy −∫_0 ^1 (1+y)ln(1+y)dy I= 2ln2 −(1/2) − ∫_0 ^1 (1+y)ln(1+y)dy the ch.1+y=t give ∫_0 ^1 (1+y)ln(1+y)dy= ∫_1 ^2 tln(t)dt =[ (t^2 /2) lnt]_1 ^2 −∫_1 ^2 (t/2)dt = 2ln2 −(1/2)[(t^2 /2)]_1 ^2 =2ln2−(1/2)((3/2)) = 2ln2 −(3/4) I= 2ln2 −(1/2) −2ln2 +(3/4)= (1/4) .](Q27756.png)
| ||
Question and Answers Forum | ||
Question Number 27690 by abdo imad last updated on 12/Jan/18 | ||
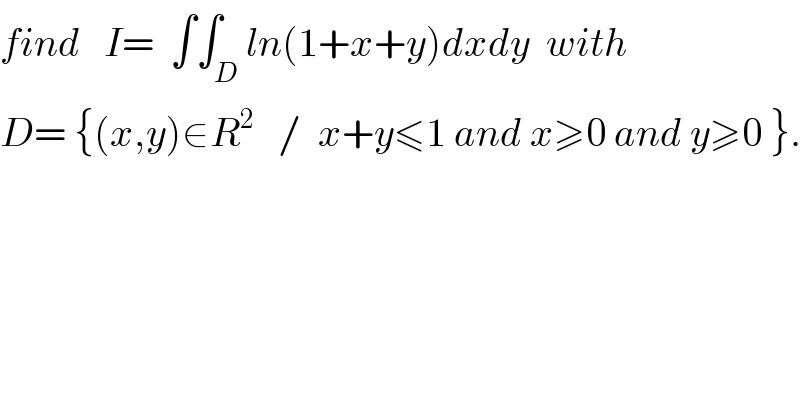 | ||
Commented by abdo imad last updated on 14/Jan/18 | ||
![0≤x≤1−y and 0≤y≤1 so I = ∫_0 ^1 ( ∫_0 ^(1−y) ln(1+x+y)dx)dy but the ch. 1+x+y =t give ∫_0 ^(1−y) ln(1+x +y)dx= ∫_(1+y) ^2 lnt dt = [tlnt −t]_(1+y) ^2 = 2ln2 −2 −(1+y)ln(1+y) +1+y =2ln2 −1 +y −(1+y)ln(1+y) I= ∫_0 ^1 (2ln2−1)dy +∫_0 ^1 ydy −∫_0 ^1 (1+y)ln(1+y)dy I= 2ln2 −(1/2) − ∫_0 ^1 (1+y)ln(1+y)dy the ch.1+y=t give ∫_0 ^1 (1+y)ln(1+y)dy= ∫_1 ^2 tln(t)dt =[ (t^2 /2) lnt]_1 ^2 −∫_1 ^2 (t/2)dt = 2ln2 −(1/2)[(t^2 /2)]_1 ^2 =2ln2−(1/2)((3/2)) = 2ln2 −(3/4) I= 2ln2 −(1/2) −2ln2 +(3/4)= (1/4) .](Q27756.png) | ||