
Question and Answers Forum
Question Number 27691 by abdo imad last updated on 12/Jan/18
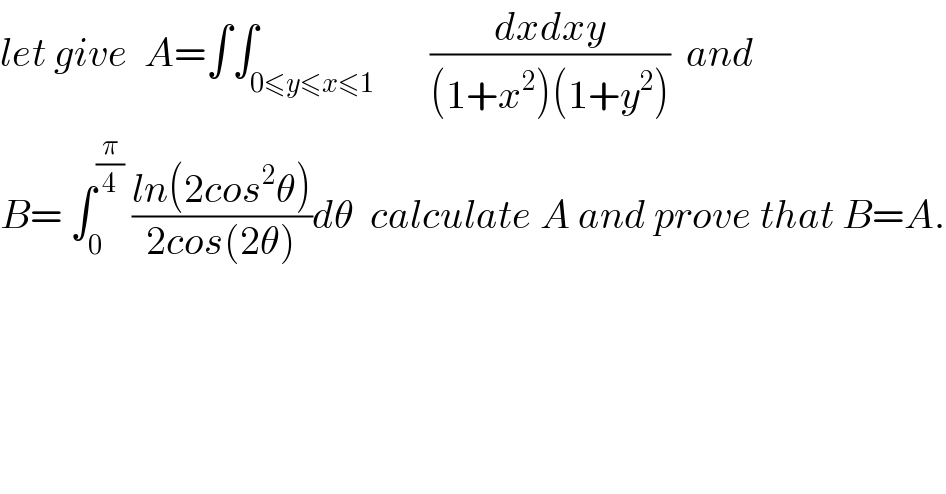
Commented by abdo imad last updated on 19/Jan/18
![A= ∫_0 ^1 (∫_0 ^x (dy/(1+y^2 ))) (dx/(1+x^2 )) = ∫_0 ^1 ((arctanx)/(1+x^2 ))dx by parts A= [actanx.arctanx]_0 ^1 − ∫_0 ^1 arctanx (dx/(1+x^2 )) 2A=(π^2 /(16)) ⇒ A= (π^2 /(32)) B= ∫_0 ^(π/4) ((ln(2((1+cos(2θ))/2)))/(2cos(2θ)))dθ= ∫_0 ^(π/4) ((ln(1+cos(2θ)))/(2cos(2θ)))dθ = ∫_0 ^(π/2) ((ln(1+cost))/(2cost)) (dt/2) = (1/4) ∫_0 ^(π/2) ((ln(1+cost))/(cost))dt let introduce F(x)= ∫_0 ^(π/2) ((ln(1+xcost))/(cost))dt with −1<x<1 F^′ (x)= ∫_0 ^(π/2) (dt/(1+xcost)) the ch. tan((t/2))=u give F^ (x)= ∫_0 ^(1 ) (1/(1+x((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 ))= ∫_0 ^1 ((2du)/(1+u^2 +x −xu^2 )) = ∫_0 ^1 ((2du)/((1−x)u^2 +1+x)) = (2/(1−x)) ∫_0 ^1 (du/(u^2 +((1+x)/(1−x)))) the ch. u=(√((1+x)/(1−x)))t give F^ (x)= (2/(1−x)) ∫_0 ^((√(1−x))/(√(1+x ))) (1/(((1+x)/(1−x))(1+u^2 ))) ((√(1+x))/(√(1−x)))dt = (2/(1−x)) ((1−x)/(1+x)) ((√(1+x))/(√(1−x))) ∫_0 ^((√(1−x))/(√(1+x))) (dt/(1+t^2 )) = (2/(√(1−x^2 ))) arctan((√((1−x)/(1+x)))) but with x=cosθ arctan((√((1−x)/(1+x))))=arctan(tan((θ/2)))= (θ/2) F^ (x)=(2/(√(1−x^2 ))) ((arcosx)/2)= ((arcosx)/(√(1−x^2 ))) F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt +λ ( λ=F(0)=0) ⇒ F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt B= (1/4) F(1)= (1/4) ∫_0 ^(1 ) ((arcost)/(√(1−t^2 )))dt by parts let put I= ∫_0 ^1 ((arcost)/(√(1−t^2 ))) dt by parts I= −arcost.arcost]_0 ^1 − ∫_0 ^1 (−arcost) ((−dt)/(√(1−t^2 ))) 2I= (π^2 /4) ⇒ I= (π^2 /8) ⇒ F(1)= (π^2 /8) and B= (π^2 /(32)) =A. for F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt let integrate by parts F(x)= −arcot arcost]_0 ^x − ∫_0 ^x (−arcosx) ((−dt)/(√(1−x^2 ))) = (π^2 /4) −(arcosx)^2 −F(x) ⇒ F(x)= (π^2 /8) −(1/2) (arcosx)^2 so ∫_0 ^(π/2) ((ln(1+xcost))/(cost))dt = (π^2 /8) − (1/2) (arcosx)^2 .](Q28046.png)
| ||
Question and Answers Forum | ||
Question Number 27691 by abdo imad last updated on 12/Jan/18 | ||
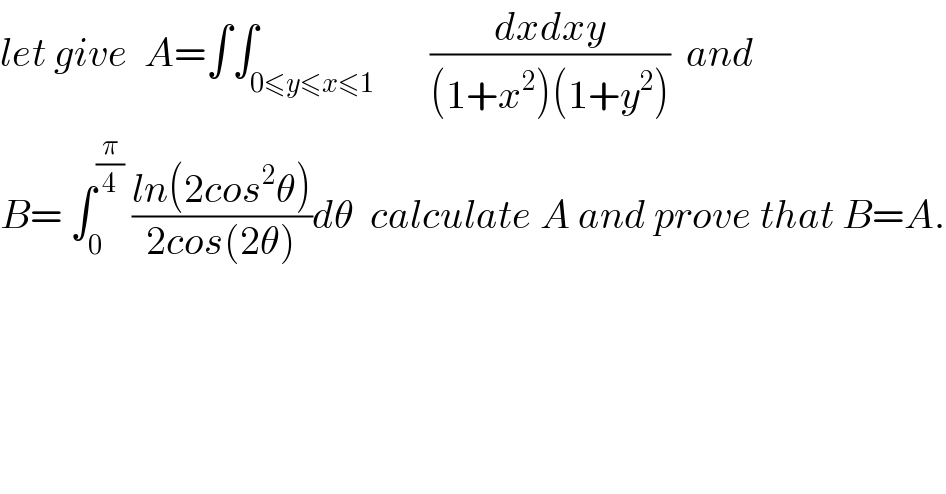 | ||
Commented by abdo imad last updated on 19/Jan/18 | ||
![A= ∫_0 ^1 (∫_0 ^x (dy/(1+y^2 ))) (dx/(1+x^2 )) = ∫_0 ^1 ((arctanx)/(1+x^2 ))dx by parts A= [actanx.arctanx]_0 ^1 − ∫_0 ^1 arctanx (dx/(1+x^2 )) 2A=(π^2 /(16)) ⇒ A= (π^2 /(32)) B= ∫_0 ^(π/4) ((ln(2((1+cos(2θ))/2)))/(2cos(2θ)))dθ= ∫_0 ^(π/4) ((ln(1+cos(2θ)))/(2cos(2θ)))dθ = ∫_0 ^(π/2) ((ln(1+cost))/(2cost)) (dt/2) = (1/4) ∫_0 ^(π/2) ((ln(1+cost))/(cost))dt let introduce F(x)= ∫_0 ^(π/2) ((ln(1+xcost))/(cost))dt with −1<x<1 F^′ (x)= ∫_0 ^(π/2) (dt/(1+xcost)) the ch. tan((t/2))=u give F^ (x)= ∫_0 ^(1 ) (1/(1+x((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 ))= ∫_0 ^1 ((2du)/(1+u^2 +x −xu^2 )) = ∫_0 ^1 ((2du)/((1−x)u^2 +1+x)) = (2/(1−x)) ∫_0 ^1 (du/(u^2 +((1+x)/(1−x)))) the ch. u=(√((1+x)/(1−x)))t give F^ (x)= (2/(1−x)) ∫_0 ^((√(1−x))/(√(1+x ))) (1/(((1+x)/(1−x))(1+u^2 ))) ((√(1+x))/(√(1−x)))dt = (2/(1−x)) ((1−x)/(1+x)) ((√(1+x))/(√(1−x))) ∫_0 ^((√(1−x))/(√(1+x))) (dt/(1+t^2 )) = (2/(√(1−x^2 ))) arctan((√((1−x)/(1+x)))) but with x=cosθ arctan((√((1−x)/(1+x))))=arctan(tan((θ/2)))= (θ/2) F^ (x)=(2/(√(1−x^2 ))) ((arcosx)/2)= ((arcosx)/(√(1−x^2 ))) F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt +λ ( λ=F(0)=0) ⇒ F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt B= (1/4) F(1)= (1/4) ∫_0 ^(1 ) ((arcost)/(√(1−t^2 )))dt by parts let put I= ∫_0 ^1 ((arcost)/(√(1−t^2 ))) dt by parts I= −arcost.arcost]_0 ^1 − ∫_0 ^1 (−arcost) ((−dt)/(√(1−t^2 ))) 2I= (π^2 /4) ⇒ I= (π^2 /8) ⇒ F(1)= (π^2 /8) and B= (π^2 /(32)) =A. for F(x)= ∫_0 ^x ((arcost)/(√(1−t^2 )))dt let integrate by parts F(x)= −arcot arcost]_0 ^x − ∫_0 ^x (−arcosx) ((−dt)/(√(1−x^2 ))) = (π^2 /4) −(arcosx)^2 −F(x) ⇒ F(x)= (π^2 /8) −(1/2) (arcosx)^2 so ∫_0 ^(π/2) ((ln(1+xcost))/(cost))dt = (π^2 /8) − (1/2) (arcosx)^2 .](Q28046.png) | ||