Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2776 by Filup last updated on 27/Nov/15

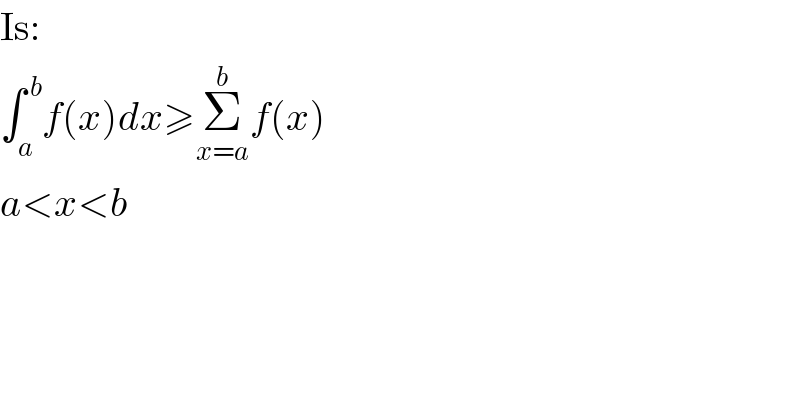
Is: ∫_a ^( b) f(x)dx≥Σ_(x=a) ^b f(x) a<x<b

$$\mathrm{Is}: \\ $$ $$\int_{{a}} ^{\:{b}} {f}\left({x}\right){dx}\geqslant\underset{{x}={a}} {\overset{{b}} {\sum}}{f}\left({x}\right) \\ $$ $${a}<{x}<{b} \\ $$

Commented byFilup last updated on 27/Nov/15

That is what I would assume

$$\mathrm{That}\:\mathrm{is}\:\mathrm{what}\:\mathrm{I}\:\mathrm{would}\:\mathrm{assume} \\ $$

Commented byFilup last updated on 27/Nov/15

This is interesting. I was curious and didn′t realise there is so much to consider I was thinking more generally. Lets say f(x)=ax^i +bx^(i−1) +...+x^1 +k or f(x)=Σ_(i=1) ^n a_i x^i or something as simple as f(x)=ax^2 +bx+c

$$\mathrm{This}\:\mathrm{is}\:\mathrm{interesting}.\:\mathrm{I}\:\mathrm{was}\:\mathrm{curious}\:\mathrm{and} \\ $$ $$\mathrm{didn}'\mathrm{t}\:\mathrm{realise}\:\mathrm{there}\:\mathrm{is}\:\mathrm{so}\:\mathrm{much}\:\mathrm{to}\:\mathrm{consider} \\ $$ $$ \\ $$ $$\mathrm{I}\:\mathrm{was}\:\mathrm{thinking}\:\mathrm{more}\:\mathrm{generally}.\:\mathrm{Lets}\:\mathrm{say} \\ $$ $${f}\left({x}\right)={ax}^{{i}} +{bx}^{{i}−\mathrm{1}} +...+{x}^{\mathrm{1}} +{k} \\ $$ $$\mathrm{or}\:{f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{i}} \\ $$ $${or}\:{something}\:{as}\:{simple}\:{as} \\ $$ $${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$ $$ \\ $$ $$ \\ $$

Commented byYozzi last updated on 27/Nov/15

What does Σ_(x=a) ^b f(x) mean? Is it implying that a,b∈Z? If you′re trying to say to add up all values of f(x) for f(x) being continuous and positive in the interval a<x<b, Σ_(x=a) ^b f(x) is divergent since the set X={x∈R∣a<x<b} has non−finite cardinality. If f(x) is continous and positive for a<x<b the integral ∫_a ^b f(x)dx is finite and positive. The inequality would not hold. Alternatively, f(x) could be such that the value of Σ_(x=a) ^b f(x) is −∞. In this case the inequality holds since ∫_a ^b f(x)dx is finite.

$${What}\:{does}\:\underset{{x}={a}} {\overset{{b}} {\sum}}{f}\left({x}\right)\:{mean}?\:{Is}\:{it}\:{implying} \\ $$ $${that}\:{a},{b}\in\mathbb{Z}?\:{If}\:{you}'{re}\:{trying}\:{to}\:{say} \\ $$ $${to}\:{add}\:{up}\:{all}\:{values}\:{of}\:{f}\left({x}\right)\:{for} \\ $$ $${f}\left({x}\right)\:{being}\:{continuous}\:{and}\:{positive}\:{in}\:{the} \\ $$ $${interval}\:{a}<{x}<{b},\:\underset{{x}={a}} {\overset{{b}} {\sum}}{f}\left({x}\right)\:{is}\:{divergent} \\ $$ $${since}\:{the}\:{set}\:{X}=\left\{{x}\in\mathbb{R}\mid{a}<{x}<{b}\right\} \\ $$ $${has}\:{non}−{finite}\:{cardinality}.\: \\ $$ $${If}\:{f}\left({x}\right)\:{is}\:{continous}\:{and}\:{positive}\:{for}\:{a}<{x}<{b} \\ $$ $${the}\:{integral}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:{is}\:{finite}\:{and} \\ $$ $${positive}.\:{The}\:{inequality}\:{would}\:{not} \\ $$ $${hold}. \\ $$ $${Alternatively},\:{f}\left({x}\right)\:{could}\:{be}\:{such}\:{that}\:{the}\:{value} \\ $$ $${of}\:\underset{{x}={a}} {\overset{{b}} {\sum}}{f}\left({x}\right)\:{is}\:−\infty.\:{In}\:{this}\:{case}\:{the} \\ $$ $${inequality}\:{holds}\:{since}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$ $${is}\:{finite}. \\ $$

Commented byprakash jain last updated on 27/Nov/15

if f(x) is defined only over finite subset. Isn′t ∫_D f(x)dx=0 ? Assuming ∣f(x)∣ <M ∀x∈D.

$$\mathrm{if}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{defined}\:\mathrm{only}\:\mathrm{over}\:\mathrm{finite}\:\mathrm{subset}. \\ $$ $$\mathrm{Isn}'\mathrm{t}\:\int_{{D}} {f}\left({x}\right){dx}=\mathrm{0}\:? \\ $$ $$\mathrm{Assuming}\:\mid{f}\left({x}\right)\mid\:<\mathrm{M}\:\:\forall{x}\in\mathrm{D}. \\ $$

Commented by123456 last updated on 27/Nov/15

if you take f(x)= { ((g(x) x∈D)),((0 x∉D)) :} where D⊂[a,b] is a finite subset i think that Σf(x) can converge

$$\mathrm{if}\:\mathrm{you}\:\mathrm{take}\:{f}\left({x}\right)=\begin{cases}{{g}\left({x}\right)\:\:\:\:{x}\in\mathrm{D}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:{x}\notin\mathrm{D}}\end{cases} \\ $$ $$\mathrm{where}\:\mathrm{D}\subset\left[{a},{b}\right]\:\mathrm{is}\:\mathrm{a}\:\mathrm{finite}\:\mathrm{subset} \\ $$ $$\mathrm{i}\:\mathrm{think}\:\mathrm{that}\:\Sigma{f}\left({x}\right)\:\mathrm{can}\:\mathrm{converge} \\ $$

Commented by123456 last updated on 27/Nov/15

yes, so if Σ_(x∈[a,b]) f(x) converge them ∫_a ^b f(x)dx=0 (assuming ∣f(x)∣≤M,x∈D)

$$\mathrm{yes},\:\mathrm{so}\:\mathrm{if}\:\underset{{x}\in\left[{a},{b}\right]} {\sum}{f}\left({x}\right)\:\mathrm{converge}\:\mathrm{them} \\ $$ $$\underset{{a}} {\overset{{b}} {\int}}{f}\left({x}\right){dx}=\mathrm{0}\:\:\left(\mathrm{assuming}\:\mid{f}\left({x}\right)\mid\leqslant\mathrm{M},{x}\in\mathrm{D}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com