
Question Number 27781 by abdo imad last updated on 14/Jan/18
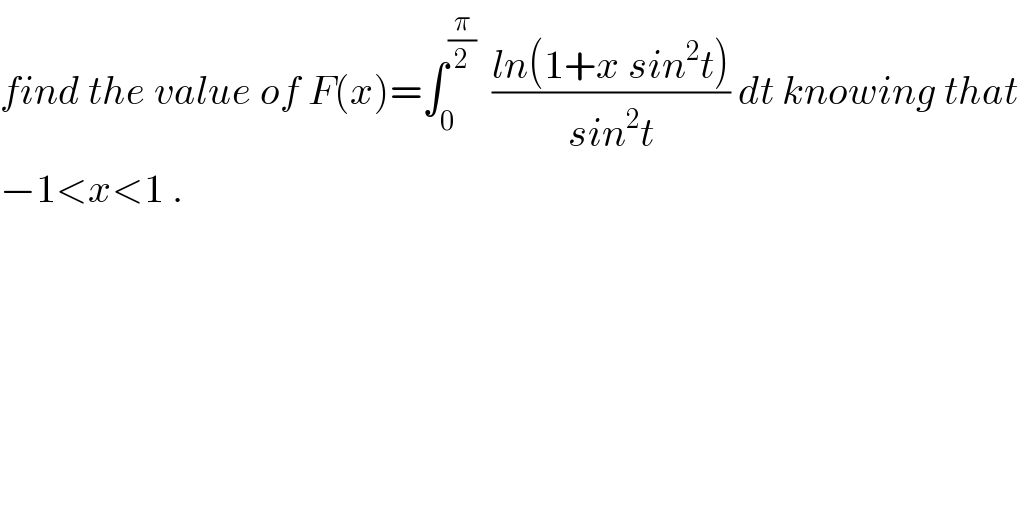
$${find}\:{the}\:{value}\:{of}\:{F}\left({x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{ln}\left(\mathrm{1}+{x}\:{sin}^{\mathrm{2}} {t}\right)}{{sin}^{\mathrm{2}} {t}}\:{dt}\:{knowing}\:{that} \\ $$ $$−\mathrm{1}<{x}<\mathrm{1}\:. \\ $$
Commented byabdo imad last updated on 18/Jan/18
![after verifying that F is derivable on ]−1,1[ F^(,′) (x)= ∫_0 ^(π/2) ((sin^2 t)/(sin^2 t(1+x sin^2 t)))dt = ∫_0 ^(π/(2 )) (dt/(1+x sin^2 t))= ∫_0 ^(π/2) (dt/(1+x ((1−cos(2t))/2))) = ∫_0 ^(π/2) ((2dt)/(2 +x −x cos(2t))) let use the ch. 2t=θ F^ (x)= ∫_0 ^π (dθ/(2+x −x cosθ)) then the ch. tan((θ/2))=t give F^ (x)= ∫_0 ^(+∝) (1/(2+x −x ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = ∫_0 ^(+∝) ((2dt)/((2+x)(1+t^2 ) −x +xt^2 )) = ∫_0 ^(+∝) ((2dt)/(2+x +(2+2x)t^2 −x))= ∫_0 ^(+∝) (dt/(1+(1+x)t^2 )) ch. u=(√(1+x))t = ∫_0 ^(+∝) (du/((√(1+x))( 1+u^2 ))) = (π/(2(√(1+x)))) ⇒ F(x)= (π/2) ∫_0 ^x (dt/(√(1+t))) +λ F(x)= π(√(1+x)) +λ and λ = F(0)−π =−π so F(x)= π( (√(1+x)) −1) .](Q28037.png)
$$\left.{after}\:{verifying}\:{that}\:\:{F}\:{is}\:{derivable}\:{on}\:\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$ $${F}^{,'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}^{\mathrm{2}} {t}}{{sin}^{\mathrm{2}} {t}\left(\mathrm{1}+{x}\:{sin}^{\mathrm{2}} {t}\right)}{dt} \\ $$ $$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}\:}} \:\:\:\:\:\frac{{dt}}{\mathrm{1}+{x}\:{sin}^{\mathrm{2}} {t}}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{x}\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}} \\ $$ $$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}\:+{x}\:−{x}\:{cos}\left(\mathrm{2}{t}\right)}\:\:{let}\:{use}\:{the}\:{ch}.\:\mathrm{2}{t}=\theta \\ $$ $${F}^{} \left({x}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\:\:\:\frac{{d}\theta}{\mathrm{2}+{x}\:−{x}\:{cos}\theta}\:{then}\:{the}\:{ch}.\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={t}\:{give} \\ $$ $${F}^{} \left({x}\right)=\:\:\int_{\mathrm{0}} ^{+\propto} \:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}+{x}\:−{x}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$ $$=\:\int_{\mathrm{0}} ^{+\propto} \:\:\:\:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{2}+{x}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:−{x}\:+{xt}^{\mathrm{2}} } \\ $$ $$=\:\int_{\mathrm{0}} ^{+\propto} \:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}+{x}\:+\left(\mathrm{2}+\mathrm{2}{x}\right){t}^{\mathrm{2}} \:−{x}}=\:\int_{\mathrm{0}} ^{+\propto} \:\:\:\:\frac{{dt}}{\mathrm{1}+\left(\mathrm{1}+{x}\right){t}^{\mathrm{2}} }\:\:\:{ch}.\:{u}=\sqrt{\mathrm{1}+{x}}{t} \\ $$ $$=\:\int_{\mathrm{0}} ^{+\propto} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{du}}{\sqrt{\mathrm{1}+{x}}\left(\:\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{1}+{x}}} \\ $$ $$\Rightarrow\:{F}\left({x}\right)=\:\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\sqrt{\mathrm{1}+{t}}}\:\:+\lambda\:\:\:\:\:\:\:\:\: \\ $$ $${F}\left({x}\right)=\:\pi\sqrt{\mathrm{1}+{x}}\:\:\:+\lambda\:\:{and}\:\lambda\:\:=\:{F}\left(\mathrm{0}\right)−\pi\:=−\pi\:{so} \\ $$ $${F}\left({x}\right)=\:\pi\left(\:\sqrt{\mathrm{1}+{x}}\:\:−\mathrm{1}\right)\:\:\:. \\ $$
