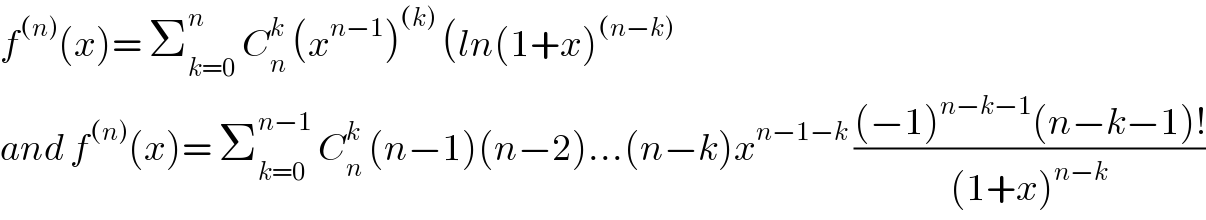Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 27790 by abdo imad last updated on 14/Jan/18

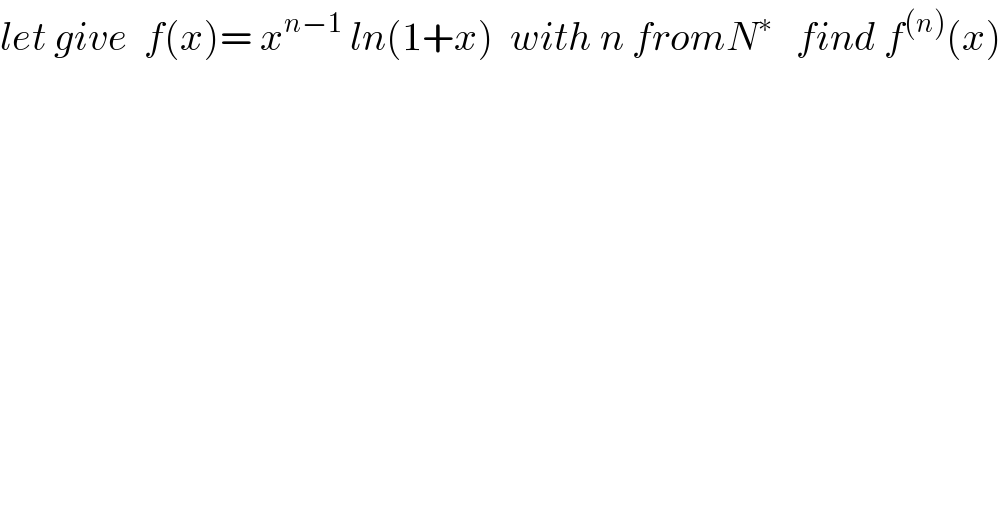
let give f(x)= x^(n−1) ln(1+x) with n fromN^∗ find f^((n)) (x)

$${let}\:{give}\:\:{f}\left({x}\right)=\:{x}^{{n}−\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}\right)\:\:{with}\:{n}\:{fromN}^{\ast} \:\:\:{find}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$

Commented by abdo imad last updated on 15/Jan/18

by leibnitz formule f^((n)) (x)= Σ_(k=0) ^n (x^(n−1) )^((k)) (ln(1+x))^((n−k)) and for p≤n (x^n )^((p)) =n(n−1)...(n−p+1)x^(n−p) so for k∈[[0,n−1]] (x^(n−1) )^k =(n−1)(n−2)....(n−1−k +1)x^(n−1−k) =(n−1)(n−2)...(n−k) x^(n−1−k) and we have ln(1+x)^((p)) =(((−1)^(p−1) (p−1)!)/((1+x)^p )) for p≥1 ⇒ f^((n)) (x)= Σ_(k=0) ^(n−1) (n−1)(n−2)...(n−k) x^(n−1−k) (((−1)^(n−k−1) (n−k−1)!)/((1+x)^(n−k) )) ( (x^(n−1) )^((n)) =0)

$$\:{by}\:{leibnitz}\:{formule}\:{f}^{\left({n}\right)} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \left({x}^{{n}−\mathrm{1}} \right)^{\left({k}\right)} \left({ln}\left(\mathrm{1}+{x}\right)\right)^{\left({n}−{k}\right)} \\ $$$$\:{and}\:{for}\:{p}\leqslant{n}\:\:\:\:\left({x}^{{n}} \right)^{\left({p}\right)} ={n}\left({n}−\mathrm{1}\right)...\left({n}−{p}+\mathrm{1}\right){x}^{{n}−{p}} \:{so}\:{for} \\ $$$${k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\:\:\:\left({x}^{{n}−\mathrm{1}} \right)^{{k}} =\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)....\left({n}−\mathrm{1}−{k}\:+\mathrm{1}\right){x}^{{n}−\mathrm{1}−{k}} \\ $$$$=\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−{k}\right)\:{x}^{{n}−\mathrm{1}−{k}} \:\: \\ $$$${and}\:{we}\:{have}\:\:\:{ln}\left(\mathrm{1}+{x}\right)^{\left({p}\right)} =\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} \left({p}−\mathrm{1}\right)!}{\left(\mathrm{1}+{x}\right)^{{p}} }\:{for}\:{p}\geqslant\mathrm{1} \\ $$$$\Rightarrow\:{f}^{\left({n}\right)} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−{k}\right)\:{x}^{{n}−\mathrm{1}−{k}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{k}−\mathrm{1}} \left({n}−{k}−\mathrm{1}\right)!}{\left(\mathrm{1}+{x}\right)^{{n}−{k}} } \\ $$$$\left(\:\:\:\:\left({x}^{{n}−\mathrm{1}} \right)^{\left({n}\right)} =\mathrm{0}\right) \\ $$$$ \\ $$

Commented by abdo imad last updated on 15/Jan/18

f^((n)) (x)= Σ_(k=0) ^n C_n ^k (x^(n−1) )^((k)) (ln(1+x)^((n−k)) and f^((n)) (x)= Σ_(k=0) ^(n−1) C_n ^k (n−1)(n−2)...(n−k)x^(n−1−k) (((−1)^(n−k−1) (n−k−1)!)/((1+x)^(n−k) ))

$${f}^{\left({n}\right)} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({x}^{{n}−\mathrm{1}} \right)^{\left({k}\right)} \:\left({ln}\left(\mathrm{1}+{x}\right)^{\left({n}−{k}\right)} \right. \\ $$$${and}\:{f}^{\left({n}\right)} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{k}} \:\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)...\left({n}−{k}\right){x}^{{n}−\mathrm{1}−{k}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{k}−\mathrm{1}} \left({n}−{k}−\mathrm{1}\right)!}{\left(\mathrm{1}+{x}\right)^{{n}−{k}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com