
Question and Answers Forum
Question Number 27792 by abdo imad last updated on 14/Jan/18
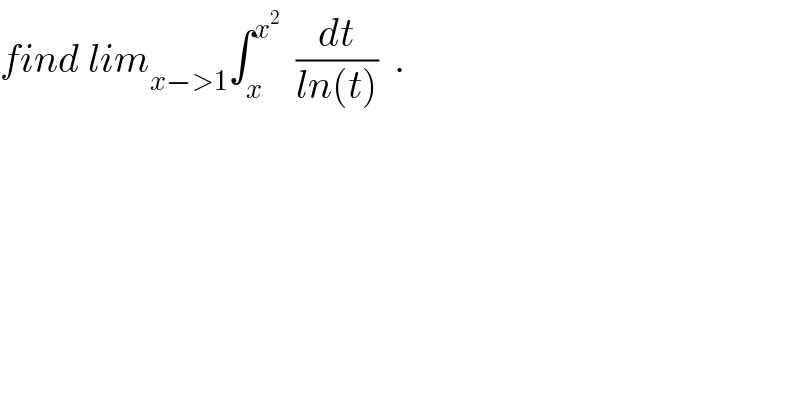
Commented byabdo imad last updated on 15/Jan/18
![if f continue in [a,b] and g integrable in [a,b]∃ c∈]a,b[/ ∫_a ^b f(x)g(x)dx= f(c) ∫_a ^b g(x)dx so ∃ c_x ∈]x,x^2 [ / ∫_x ^x^2 (dt/(lnt)) = (1/(ln c)) ∫_x ^x^2 dx = ((x^2 −x)/(lnc_x ))= ((x(x−1))/(ln(c_x )))but x−>1⇔c_x −>1 so lim_(x−>1) ∫_x ^x^2 (dt/(lnt))= lim_c_(x−>1) ((c_x (c_x ^ −1))/(lnc_x )) lim_c_(x−>1) (1/((lnc_x )/(c_x −1)))= 1 . (we can confuse x and c_x brcause x∈V(1) and c_x ∈ V(1).](Q27829.png)
Commented byprakash jain last updated on 16/Jan/18

Commented byabdo imad last updated on 16/Jan/18
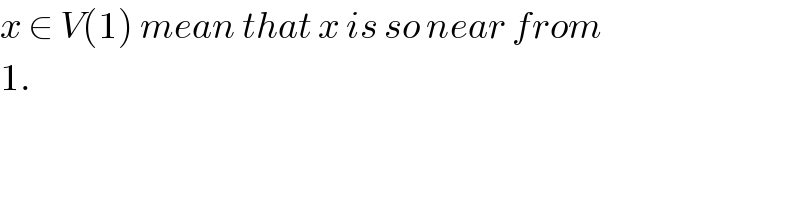
| ||
Question and Answers Forum | ||
Question Number 27792 by abdo imad last updated on 14/Jan/18 | ||
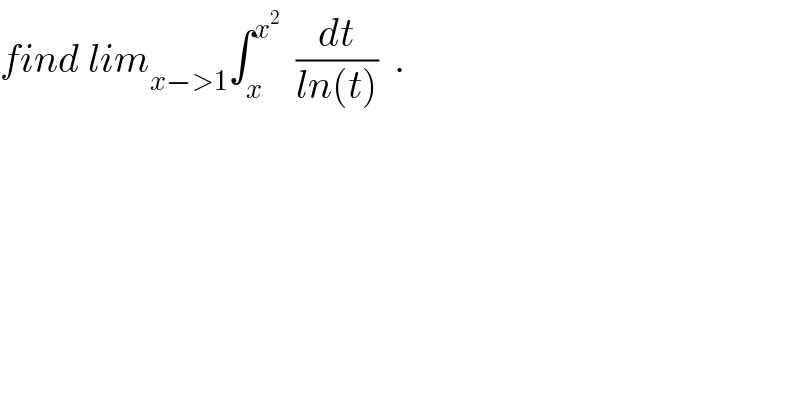 | ||
Commented byabdo imad last updated on 15/Jan/18 | ||
![if f continue in [a,b] and g integrable in [a,b]∃ c∈]a,b[/ ∫_a ^b f(x)g(x)dx= f(c) ∫_a ^b g(x)dx so ∃ c_x ∈]x,x^2 [ / ∫_x ^x^2 (dt/(lnt)) = (1/(ln c)) ∫_x ^x^2 dx = ((x^2 −x)/(lnc_x ))= ((x(x−1))/(ln(c_x )))but x−>1⇔c_x −>1 so lim_(x−>1) ∫_x ^x^2 (dt/(lnt))= lim_c_(x−>1) ((c_x (c_x ^ −1))/(lnc_x )) lim_c_(x−>1) (1/((lnc_x )/(c_x −1)))= 1 . (we can confuse x and c_x brcause x∈V(1) and c_x ∈ V(1).](Q27829.png) | ||
Commented byprakash jain last updated on 16/Jan/18 | ||
 | ||
Commented byabdo imad last updated on 16/Jan/18 | ||
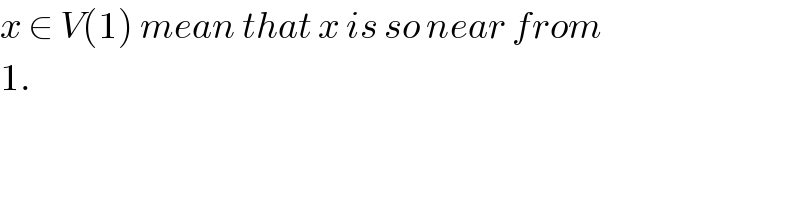 | ||