
Question Number 27804 by abdo imad last updated on 15/Jan/18
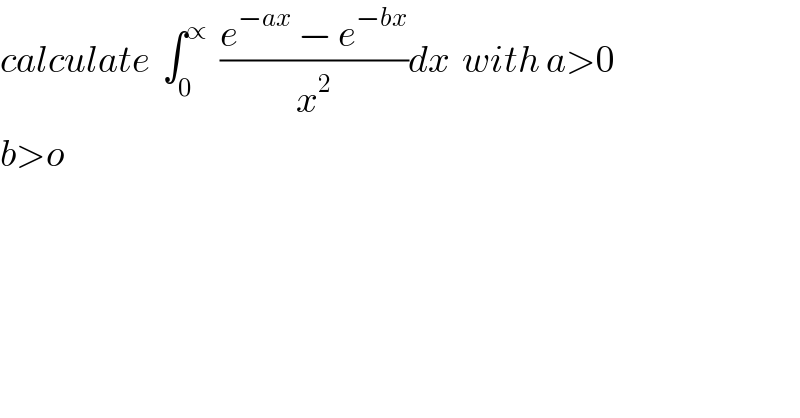
$${calculate}\:\:\int_{\mathrm{0}} ^{\propto} \:\:\frac{{e}^{−{ax}} \:−\:{e}^{−{bx}} }{{x}^{\mathrm{2}} }{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$ $${b}>{o} \\ $$
Commented byabdo imad last updated on 17/Jan/18
![let put I= ∫_0 ^∞ ((e^(−ax) −e^(−bx) )/x^2 )dx we have lim_(x→0 ) ((e^(−ax) −e^(−bx) )/x^2 ) =lim_(x→0 ) ((−a e^(−ax) +b e^(−bx) )/(2x)) =lim_(x→o) ((a^2 e^(−ax) −b^2 e^(−bx) )/2)= ((a^2 −b^2 )/2) for another side lim_(x→+∝) x^2 ((e^(−ax) −e^(−bx) )/x^2 ) =0 so the integral converges let integrate by parts u^′ =(1/x^2 ) and v= e^(−ax) −e^(−bx) I=[ −(1/x)( e^(−ax) − e^(−bx) )]_0 ^(+∝) − ∫_0 ^∞ −(1/x) ( −a e^(−ax) +b e^(−bx) )dx = b−a + ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x)dx let introduce f(t) = ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x) e^(−tx) dx with t≥0 f^′ (t)= −∫_0 ^∞ ( b e^(−bx) −a e^(−ax) ) e^(−tx) = a∫_0 ^∞ e^(−( t+a)x) dx −b∫_0 ^∞ e^(−(t+b)x) dx but ∫_0 ^∞ e^(−(t+a)x) dx=[ ((−1)/(t+a)) e^(−(t+a)x) ]_0 ^(+∝) = (1/(t+a)) and by same manner ∫_0 ^∞ e^(−(t+b)x) dx= (1/(t+b)) f^′ (t)= (a/(t+a)) − (b/(t+b)) ⇒ f(t)= aln/t+a/ −b ln/t+b/ +λ λ= lim_(t→+∝) (f(t) −aln/t+a/−bln/t+b/)=0 so f(t) = aln/t+a/ −bln/t+b/ but t≥0 and a>0 and b>0 f(t)= aln(t+a) −bln(t+b) and ∫_0 ^∞ ((b e^(−bx) − a e^(−ax) )/x)dx=f(0)= aln(a)−b lnb finally I = b−a +aln(a) −b ln(b) .](Q27963.png)
$${let}\:{put}\:\:{I}=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−{ax}} \:\:−{e}^{−{bx}} }{{x}^{\mathrm{2}} }{dx}\:\:{we}\:{have} \\ $$ $${lim}_{{x}\rightarrow\mathrm{0}\:} \:\:\:\frac{{e}^{−{ax}} \:−{e}^{−{bx}} }{{x}^{\mathrm{2}} }\:={lim}_{{x}\rightarrow\mathrm{0}\:\:} \:\:\:\frac{−{a}\:{e}^{−{ax}} \:+{b}\:{e}^{−{bx}} }{\mathrm{2}{x}} \\ $$ $$={lim}_{{x}\rightarrow{o}} \:\:\frac{{a}^{\mathrm{2}} \:{e}^{−{ax}} \:−{b}^{\mathrm{2}} {e}^{−{bx}} }{\mathrm{2}}=\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}}\:{for}\:{another}\:{side} \\ $$ $$ \\ $$ $${lim}_{{x}\rightarrow+\propto} \:{x}^{\mathrm{2}} \:\frac{{e}^{−{ax}} −{e}^{−{bx}} }{{x}^{\mathrm{2}} }\:=\mathrm{0}\:\:{so}\:{the}\:{integral}\:{converges} \\ $$ $${let}\:{integrate}\:{by}\:{parts}\:\:{u}^{'} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\:{and}\:{v}=\:{e}^{−{ax}} −{e}^{−{bx}} \\ $$ $${I}=\left[\:−\frac{\mathrm{1}}{{x}}\left(\:{e}^{−{ax}} \:−\:{e}^{−{bx}} \right)\right]_{\mathrm{0}} ^{+\propto} \:−\:\int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{{x}}\:\left(\:−{a}\:{e}^{−{ax}} \:+{b}\:{e}^{−{bx}} \right){dx} \\ $$ $$=\:{b}−{a}\:\:\:\:+\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{b}\:{e}^{−{bx}} −{a}\:{e}^{−{ax}} }{{x}}{dx}\:\:{let}\:{introduce} \\ $$ $${f}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{b}\:{e}^{−{bx}} \:−{a}\:{e}^{−{ax}} }{{x}}\:{e}^{−{tx}} \:{dx}\:\:{with}\:\:{t}\geqslant\mathrm{0} \\ $$ $${f}^{'} \left({t}\right)=\:\:−\int_{\mathrm{0}} ^{\infty} \left(\:{b}\:{e}^{−{bx}} \:−{a}\:{e}^{−{ax}} \right)\:{e}^{−{tx}} \\ $$ $$=\:{a}\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\:{t}+{a}\right){x}} {dx}\:\:−{b}\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({t}+{b}\right){x}} {dx}\:\:\:{but} \\ $$ $$\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({t}+{a}\right){x}} {dx}=\left[\:\frac{−\mathrm{1}}{{t}+{a}}\:{e}^{−\left({t}+{a}\right){x}} \right]_{\mathrm{0}} ^{+\propto} \:\:=\:\:\frac{\mathrm{1}}{{t}+{a}}\:{and}\:{by}\:{same} \\ $$ $${manner}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({t}+{b}\right){x}} {dx}=\:\:\frac{\mathrm{1}}{{t}+{b}} \\ $$ $${f}^{'} \left({t}\right)=\:\frac{{a}}{{t}+{a}}\:−\:\frac{{b}}{{t}+{b}}\:\:\Rightarrow\:{f}\left({t}\right)=\:{aln}/{t}+{a}/\:\:−{b}\:{ln}/{t}+{b}/\:+\lambda \\ $$ $$\lambda=\:{lim}_{{t}\rightarrow+\propto} \left({f}\left({t}\right)\:−{aln}/{t}+{a}/−{bln}/{t}+{b}/\right)=\mathrm{0} \\ $$ $${so}\:\:{f}\left({t}\right)\:=\:\:{aln}/{t}+{a}/\:−{bln}/{t}+{b}/\:{but}\:{t}\geqslant\mathrm{0}\:\:{and}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$ $${f}\left({t}\right)=\:{aln}\left({t}+{a}\right)\:−{bln}\left({t}+{b}\right)\:{and} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{b}\:{e}^{−{bx}} \:−\:{a}\:{e}^{−{ax}} }{{x}}{dx}={f}\left(\mathrm{0}\right)=\:{aln}\left({a}\right)−{b}\:{lnb}\:\:{finally} \\ $$ $${I}\:=\:{b}−{a}\:\:+{aln}\left({a}\right)\:−{b}\:{ln}\left({b}\right)\:\:. \\ $$ $$ \\ $$
