
Question and Answers Forum
Question Number 27828 by abdo imad last updated on 15/Jan/18
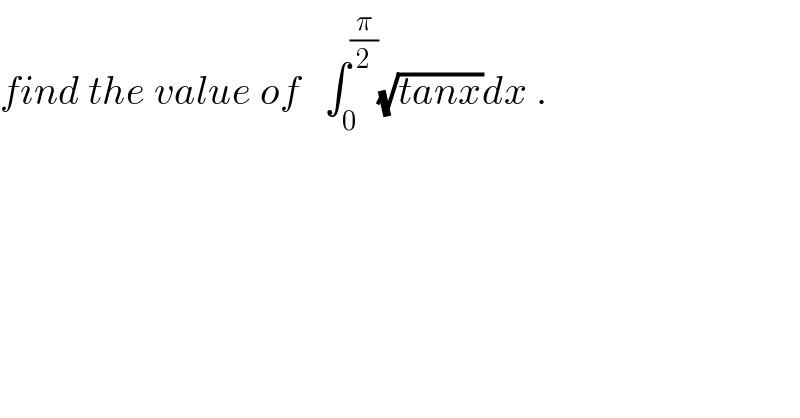
Commented by NECx last updated on 15/Jan/18
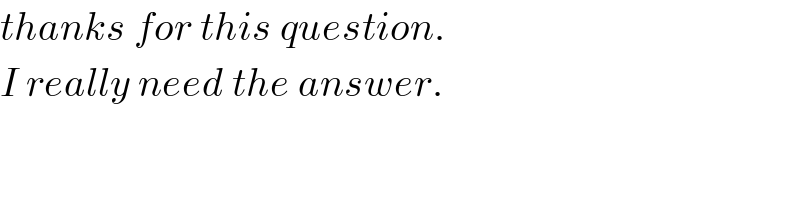
Commented by abdo imad last updated on 15/Jan/18
![let use the ch. (√(tanx))=t ⇔ tanx=t^2 ⇔ x= arctan (t^2 ) I= ∫_0 ^(π/2) (√(tanx))dx= ∫_0 ^∞ t ((2t)/(1+t^4 )) dt =∫_0 ^∝ ((2t^2 )/(1+t^4 ))dt = (1/2) ∫_(−∝) ^(+∝) ((2t^2 )/(1+t^4 ))dt let introduce the complex function f(z)= ((2z^2 )/(1+z^4 )) let find the poles of f? 1+z^4 =0⇔ z^4 = e^(i(2k+1)π) so the poles are z_(k ) = e^(i(2k+1)(π/4)) and k∈[[0,3]] we have z_0 = e^(i(π/4)) , z_1 = e^(i((3π)/4)) , z_2 = e^(i((5π)/4)) z_3 = e^(i((7π)/4)) and ∫_R^ f(z)dz= 2iπ( Res(f,z_0 ) +Res(f,z_1 )) Res(f ,z_0 )= ((2z_0 ^2 )/(4z_0 ^3 ))= (1/2) z_0 ^(−1) =(1/2) e^(−i(π/4)) Res(f,z_1 )= ((2z_1 ^2 )/(4z_1 ^3 ))=(1/2) z_1 ^(−1) =−(1/2) e^(−i((3π)/4)) =(1/2) e^(−i(π−(π/4))) = −(1/2) e^(i(π/4)) ∫_R f(z)dz=2iπ[ (1/2)( e^(−i(π/4)) −e^(i(π/4)) )]=iπ(−2i sin((π/4))) =2π ((√2)/2) =π(√2)⇒ I= (1/2) ∫_R f(z)dz= ((π(√2))/2) .](Q27865.png)
Answered by ajfour last updated on 15/Jan/18

| ||
Question and Answers Forum | ||
Question Number 27828 by abdo imad last updated on 15/Jan/18 | ||
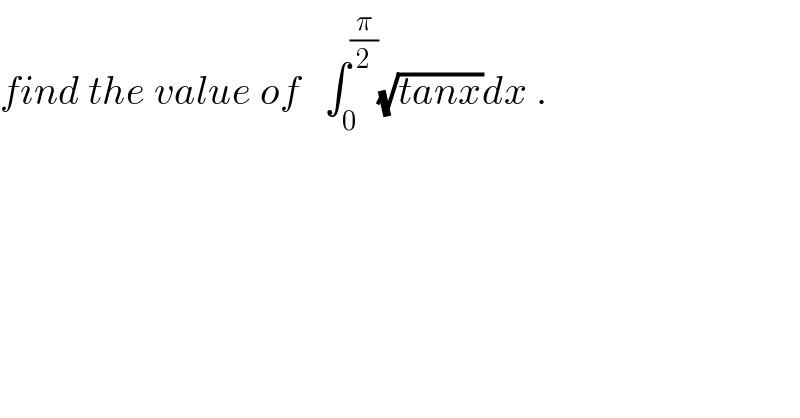 | ||
Commented by NECx last updated on 15/Jan/18 | ||
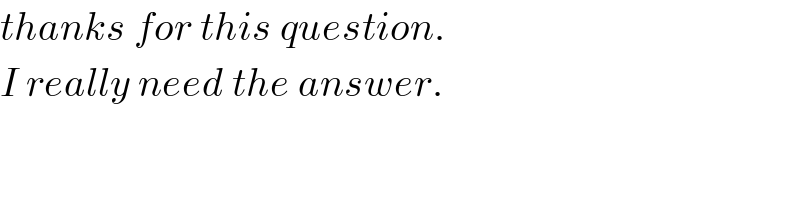 | ||
Commented by abdo imad last updated on 15/Jan/18 | ||
![let use the ch. (√(tanx))=t ⇔ tanx=t^2 ⇔ x= arctan (t^2 ) I= ∫_0 ^(π/2) (√(tanx))dx= ∫_0 ^∞ t ((2t)/(1+t^4 )) dt =∫_0 ^∝ ((2t^2 )/(1+t^4 ))dt = (1/2) ∫_(−∝) ^(+∝) ((2t^2 )/(1+t^4 ))dt let introduce the complex function f(z)= ((2z^2 )/(1+z^4 )) let find the poles of f? 1+z^4 =0⇔ z^4 = e^(i(2k+1)π) so the poles are z_(k ) = e^(i(2k+1)(π/4)) and k∈[[0,3]] we have z_0 = e^(i(π/4)) , z_1 = e^(i((3π)/4)) , z_2 = e^(i((5π)/4)) z_3 = e^(i((7π)/4)) and ∫_R^ f(z)dz= 2iπ( Res(f,z_0 ) +Res(f,z_1 )) Res(f ,z_0 )= ((2z_0 ^2 )/(4z_0 ^3 ))= (1/2) z_0 ^(−1) =(1/2) e^(−i(π/4)) Res(f,z_1 )= ((2z_1 ^2 )/(4z_1 ^3 ))=(1/2) z_1 ^(−1) =−(1/2) e^(−i((3π)/4)) =(1/2) e^(−i(π−(π/4))) = −(1/2) e^(i(π/4)) ∫_R f(z)dz=2iπ[ (1/2)( e^(−i(π/4)) −e^(i(π/4)) )]=iπ(−2i sin((π/4))) =2π ((√2)/2) =π(√2)⇒ I= (1/2) ∫_R f(z)dz= ((π(√2))/2) .](Q27865.png) | ||
Answered by ajfour last updated on 15/Jan/18 | ||
 | ||
| ||