
Question and Answers Forum
Question Number 2783 by 123456 last updated on 27/Nov/15
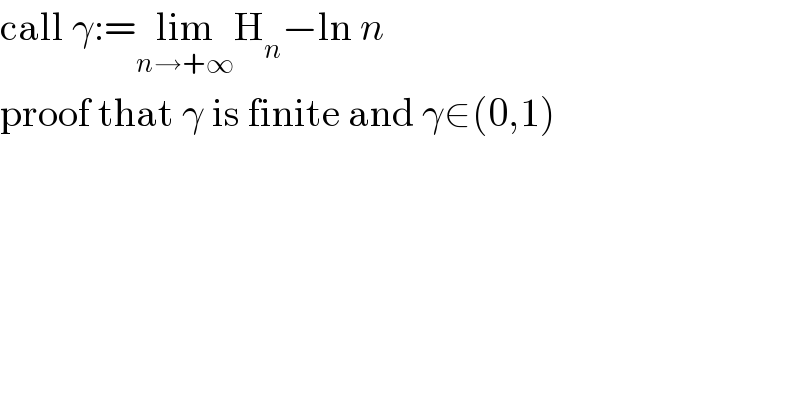
Commented by Filup last updated on 27/Nov/15
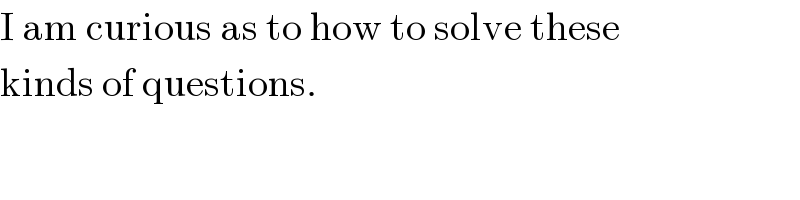
Commented by Filup last updated on 27/Nov/15
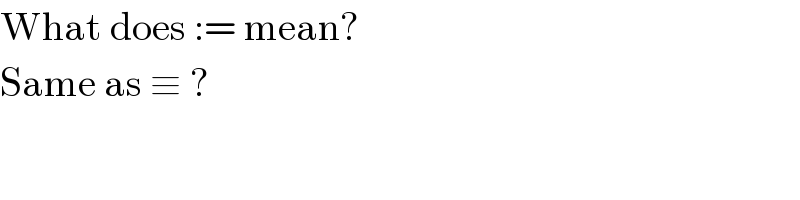
Commented by 123456 last updated on 27/Nov/15

Commented by Filup last updated on 27/Nov/15

Answered by prakash jain last updated on 27/Nov/15
![γ_n =H_n −ln n H_n =1+(1/2)+(1/3)+..+(1/n)=Σ_(i=1) ^n a_i a_i =(1/i) f(x)=(1/x) so that f(i)=a_i Since f(x) is strictly decreasing +ve function. From integral test for series ∫_N ^(M+1) f(x)dx≤Σ_(n=N) ^M f(n)≤f(N)+∫_N ^M f(x)dx ...(A) H_(n−1) ≥∫_1 ^n (1/x)dx=ln n So γ_n =H_n −ln n=(1/n)+H_(n−1) −ln n>0 ...(1) γ_(n+1) =γ_n +(1/(n+1))−ln (n+1)+ln n (1/(n+1))≤ln((n+1)/n) (comparing area of rectangles) ⇒γ_(n+1) =γ_n −[ln ((n+1)/n)−(1/(n+1))]<γ_n γ_n >0 and γ_(n+1) <γ_n So lim_(n→∞) γ_n exists and >0. γ_1 =1−ln 1=1 ∵γ_(n+1) <γ_n 0<γ<1](Q2802.png)
Commented by RasheedAhmad last updated on 29/Nov/15

Commented by 123456 last updated on 29/Nov/15
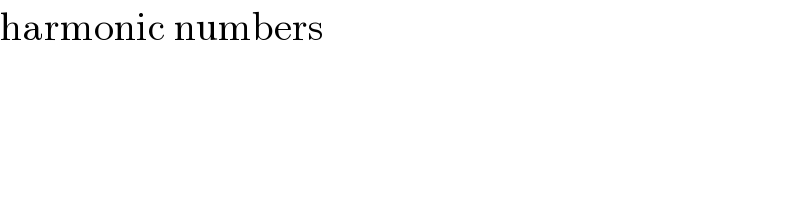
Commented by Rasheed Soomro last updated on 29/Nov/15

