(3) Find the term independ− ent of x in the expansion of ( x+(1/x))^2 (x−(1/x))^(12)


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 27884 by das47955@mail.com last updated on 16/Jan/18

$(3) Find the term independ -$ $ent of x in the expansion of$ ${(x + \frac{1}{x})}^{2} {(x - \frac{1}{x})}^{12}$
	Answered by Rasheed.Sindhi last updated on 16/Jan/18

	${(x + \frac{1}{x})}^{2} {(x - \frac{1}{x})}^{12}$ $(x^{2} + 2 + \frac{1}{x^{2}}) {(x - \frac{1}{x})}^{12}$ $- - - -$ $T_{r + 1} = (\begin{matrix} n \\ r \end{matrix}) a^{n - r} b^{r}$ $- - - - - -$ $T_{r + 1} of {(x - \frac{1}{x})}^{12}$ $T_{r + 1} = (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - r} {(- \frac{1}{x})}^{r}$ $T_{r + 1} = {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r}$ $T_{r + 1} multiplied by (x^{2} + 2 + \frac{1}{x^{2}})$ $(x^{2} + 2 + \frac{1}{x^{2}}) . T_{f + 1} = x^{2} T_{r + 1} + {2 T}_{r + 1} + (\frac{1}{x^{2}}) T_{r + 1}$ $= x^{2} {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r}$ $+ 2 {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r}$ $+ (\frac{1}{x^{2}}) {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r}$ $= {(- r)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{14 - 2 r}$ $+ 2 {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r}$ $+ {(- 1)}^{r} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{10 - 2 r}$ $When 14 - 2 r = 0 \Rightarrow r = 7$ $Free of x term 1 st part of the above$ ${(- 1)}^{7} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{14 - 2 (7)} = - (\begin{matrix} 12 \\ 7 \end{matrix}) . . (i)$ $When 12 - 2 r = 0 \Rightarrow r = 6$ $Free of x, 2 nd part of above$ $2 {(- 1)}^{6} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{12 - 2 r} = 2 (\begin{matrix} 12 \\ 6 \end{matrix}) . . . (ii)$ $When 10 - 2 r = 0 \Rightarrow r = 5$ $Free of x, 3 rd part of the above$ ${(- 1)}^{7} (\begin{matrix} 12 \\ r \end{matrix}) {(x)}^{10 - 2 r} = - (\begin{matrix} 12 \\ 5 \end{matrix}) . . . (iii)$ $Free of x term = (i) + (ii) + (iii)$ $= - (\begin{matrix} 12 \\ 7 \end{matrix}) + 2 (\begin{matrix} 12 \\ 6 \end{matrix}) - (\begin{matrix} 12 \\ 5 \end{matrix})$ $= - 792 + 2 \times 924 - 792 = 264$
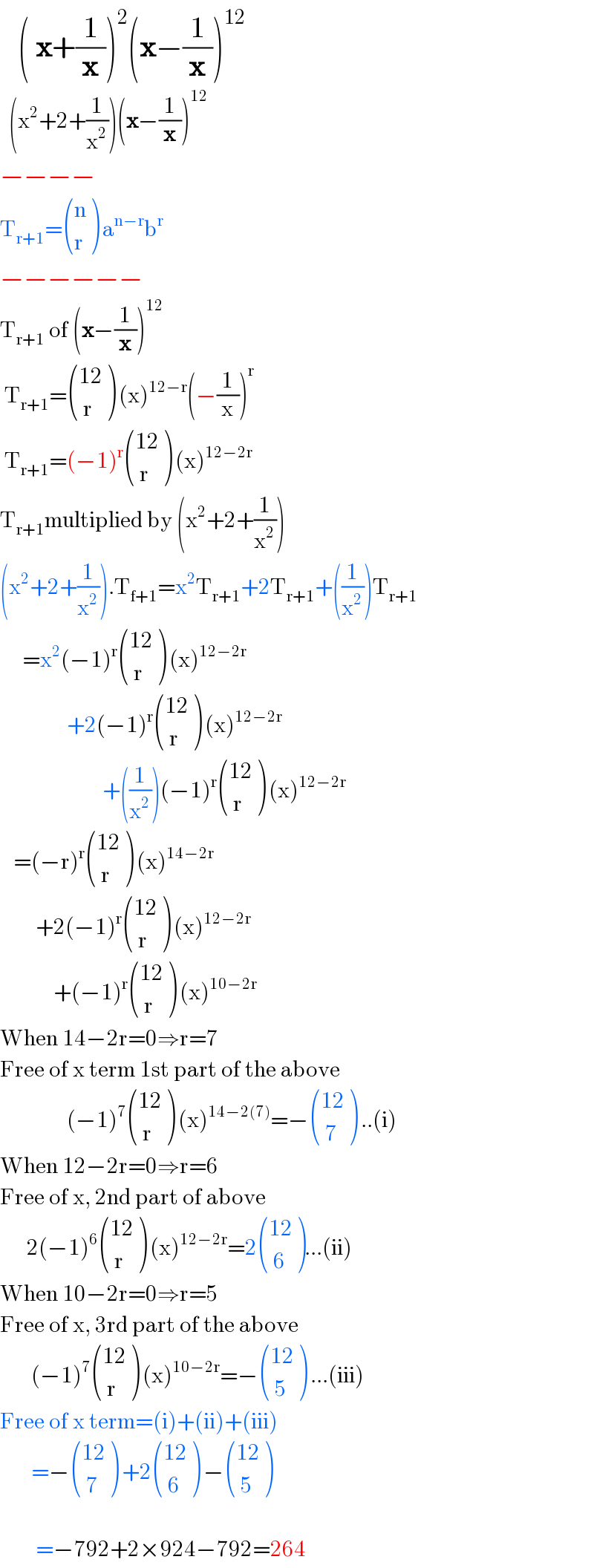
	Commented by Rasheed.Sindhi last updated on 16/Jan/18

	$Corrected now .$
	Answered by mrW2 last updated on 16/Jan/18

	${(x + \frac{1}{x})}^{2} {(x - \frac{1}{x})}^{12}$ $= \frac{1}{x^{14}} {(x^{2} + 1)}^{2} {(x^{2} - 1)}^{12}$ $= \frac{1}{x^{14}} (x^{4} + 2 x^{2} + 1) {(x^{2} - 1)}^{12}$ $= \frac{1}{x^{14}} (x^{4} + 2 x^{2} + 1) \underset{k = 0}{\sum^{12}} C_{k}^{12} x^{2 k} {(- 1)}^{12 - k}$ $t e r m i n d e p e n d e n t o f x i s :$ $\frac{1}{x^{14}} \times x^{4} \times C_{5}^{12} x^{2 \times 5} {(- 1)}^{12 - 5} + \frac{1}{x^{14}} \times 2 x^{2} \times C_{6}^{12} x^{2 \times 6} {(- 1)}^{12 - 6} + \frac{1}{x^{14}} \times 1 \times C_{7}^{12} x^{2 \times 7} {(- 1)}^{12 - 7}$ $= - C_{5}^{12} + 2 C_{6}^{12} - C_{7}^{12}$ $= - 792 + 2 \times 924 - 792$ $= 264$
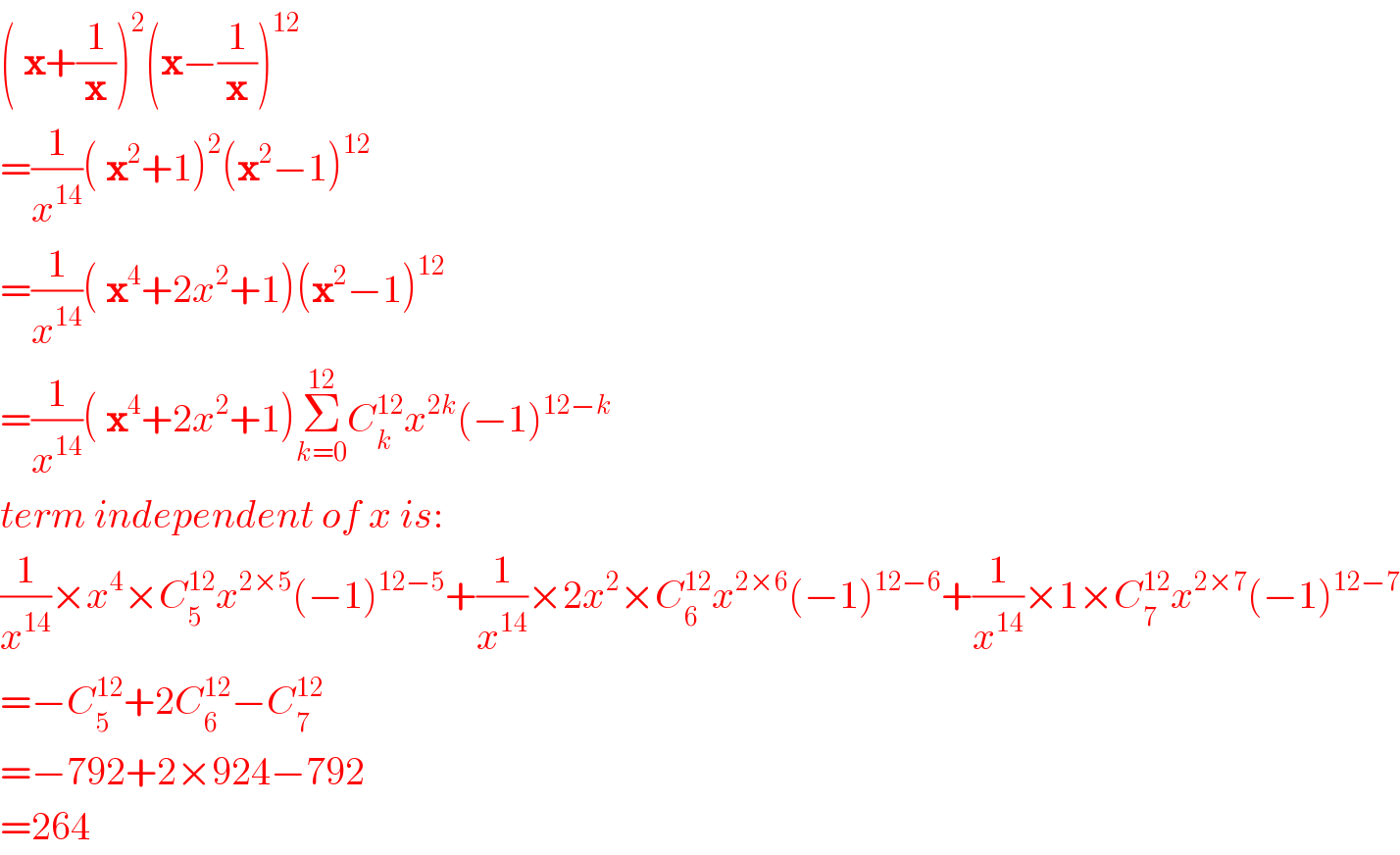
	Commented by mrW2 last updated on 16/Jan/18

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum