Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 27899 by Tinkutara last updated on 16/Jan/18

	Answered by mrW2 last updated on 17/Jan/18

	$l e t e = m a x . e l o n g a t i o n o f s p r i n g a f t e r r e l e a s e$ $k e = μ m_{A} g . . . (i)$ $\frac{1}{2} {k d}^{2} - μ m_{B} g (d + e) = \frac{1}{2} {k e}^{2} . . . (i i)$ ${k d}^{2} - 2 μ m_{B} g d - (2 μ m_{B} g + k e) e = 0$ ${k d}^{2} - 2 μ m_{B} g d - \frac{m_{A} (2 m_{B} + m_{A}) {(μ g)}^{2}}{k} = 0$ $\Rightarrow d = \frac{2 μ m_{B} g + \sqrt{{(2 μ {g m}_{B})}^{2} + 4 m_{A} (2 m_{B} + m_{A}) {(μ g)}^{2}}}{2 k}$ $\Rightarrow d = \frac{μ g (m_{A} + 2 m_{B})}{k}$ $\Rightarrow d = \frac{0.5 \times 10 (2 + 2 \times 4)}{50} = 1 m$
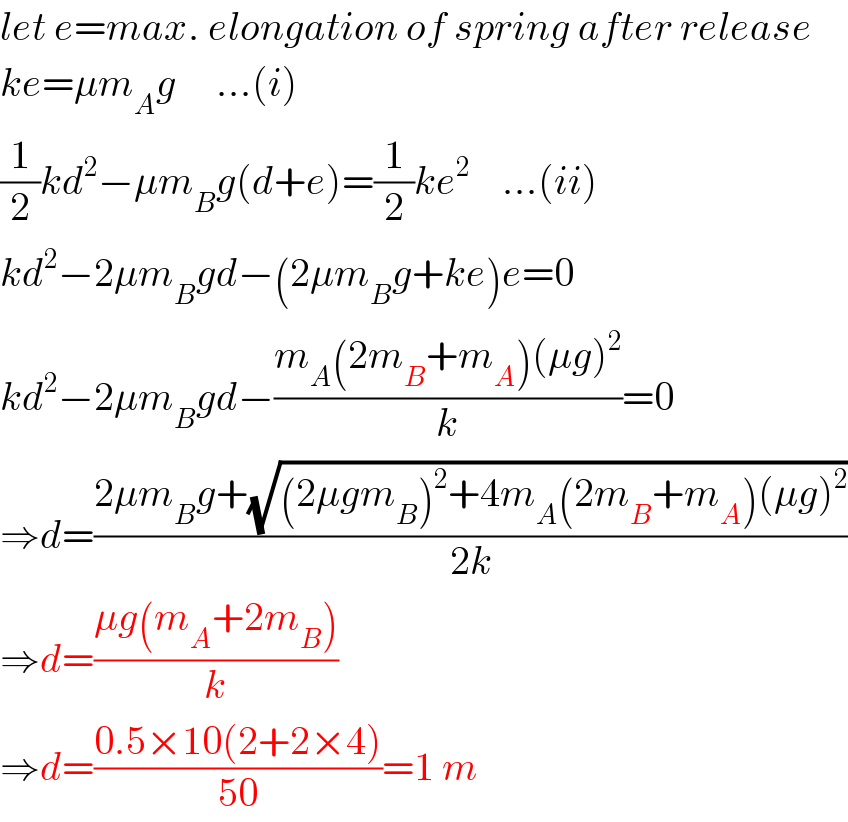
	Commented by Tinkutara last updated on 16/Jan/18

	Commented by Tinkutara last updated on 16/Jan/18
	This is the solution in book. Can you please explain this? And why your method is wrong? This question was integer type so they approximated it to 1 m.
	Commented by mrW2 last updated on 17/Jan/18

	$W h e n b l o c k A i s p r e s s e d a g a i n s t t h e$ $w a l l, t h e c o n t a c t f o r c e b e t w e e n b l o c k$ $A a n d t h e w a l l i s t h e p u s h f o r c e i n$ $s p r i n g, w h i c h i s k d .$ $W h e n b l o c k B i s r e l e a s e d, t h e c o n t a c t$ $f o r c e b t w . A a n d w a l l w i l l b e r e d u c e d$ $t i l l z e r o (s a y a t i n s t a n t t_{1}), t h e n d u e t o$ $t e n s i o n f o r c e i n s p r i n g t h e f r i c t i o n f o r c e$ $b t w . A a n d f l o o r i n c r e a s e s f r o m z e r o t i l l μ m_{A} g$ $(s a y a t i n s t a n t t_{2}), a f t e r t h a t t h e b l o c k A$ $b e g i n s t o m o v e .$ $T h e a n s w e r d e p e n d s v e r y m u c h o n h o w$ $y o u u n d e r s t a n d ‘ ‘ b l o c k A l o s e s c o n t a c t$ $t o {w a l l}^{″} .$ $M y a n s w e r i s c o r r e c t, i f m a n$ $u n d e r s t a n d s t h e l o s e o f c o n t a c t a s t h e i n s t a n t w h e n$ $b l o c k A i s a b o u t t o m o v e a w a y f r o m w a l l,$ $i . e . a t i n s t a n t t_{2}, w h e n t h e t e n s i o n f o r c e$ $i n s p r i n g j u s t o v e r c o m e s t h e s t a t i c f r i c t i o n$ $b e t w e e n b l o c k A a n d f l o o r, i . e .$ $k e = μ m_{A} g .$ $T h e a n s w e r i n b o o k i s c o r r e c t, i f m a n$ $u n d e r s t a n d s t h e l o s e o f c o n t a c t a s t h e i n s t a n t w h e n$ $t h e c o n t a c t f o r c e t o t h e w a l l b e c o m e s z e r o,$ $i . e . a t i n s t a n t t_{1} . I n t h i s c a s e t h e b l o c k$ $B m a y m o v e m a x . t o a p o s i t i o n w h e r e$ $t h e s p r i n g h a s n o e l o n g a t i o n (e = 0) s o t h a t$ $t h e s p r i n g f o r c e (a n d t h e r e f o r e t h e c o n t a c t f o r c e t o$ $w a l l) i s z e r o . T h e e n e r g y s t o r e d i n t h e$ $c o m p r e s s e d s p r i n g i s j u s t e n o u g h t o c o m p e n s a t e$ $t h e l o s e d u e t o f r i c t i o n d u r i n g t h e m o v e m e n t o f b l o c k B i n a d i s t a n c e d, i . e .$ $\frac{1}{2} {k d}^{2} = μ m_{B} g d$ $T h i s i s t h e s o l u t i o n g i v e n i n b o o k .$ $Y o u c a n a l s o g e t t h i s s o l u t i o n i f y o u p u t$ $k e = 0 i n s t e a d o f k e = μ m_{A} g i n m y e q n . (i) .$ $I {d o n}^{'} t a g r e e t h a t t h e {b o o k}^{'} s$ $a n s w e r i s t h e o n l y c o r r e c t a n s w e r .$ $B e c a u s e i t i s n o t c l e a r l y d e f i n e d w h a t$ $i s m e a n t w i t h ‘ ‘ b l o c k A l o s e s c o n t a c t$ $t o {w a l l}^{″} .$
	Commented by Tinkutara last updated on 17/Jan/18
	Thank you very much Sir! I got the answer.
	Answered by ajfour last updated on 17/Jan/18

	$k e = μ m_{A} g . . . . (i)$ $\frac{1}{2} {k d}^{2} = \frac{1}{2} {k e}^{2} + μ m_{B} g (d + e) . . . (i i)$ $f r o m (i) : e = \frac{0.5 \times 2 \times 10}{50} = \frac{1}{5}$ $r e p l a c i n g i n (i i) : e = \frac{1}{5}, k = 50$ $m_{A} = 2, m_{B} = 4$ $25 d^{2} = 1 + 20 (d + \frac{1}{5})$ $\Rightarrow 5 d^{2} - 4 d - 1 = 0$ $5 {(d - \frac{2}{5})}^{2} = \frac{9}{5}$ $d = \frac{2}{5} + \frac{3}{5} = 1 .$
	Commented by Tinkutara last updated on 17/Jan/18
	Thank you very much Sir! I got the answer.
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum